芝诺(约前490—前425年)。古希腊数学家、哲学家。他是埃利亚学派的著名哲学家巴门尼德的学生和朋友,以芝诺悖论著称
爱利亚学派的第三位哲学家芝诺,是巴门尼德的学生。

芝诺的鼎盛年大约是在公元前468年,他在哲学史中的最大贡献便是对巴门尼德的存在论思想进行了辩护。在巴门尼德看来,“存在”是不生不灭、独一无二、不变不动的,而芝诺的思想就是要否定“运动”和“多”。但芝诺的劲儿使得有点大,因矫枉过正而走入了“诡辩”的境地。这里说的“诡辩”是一种狡辩的表达方式,有意将真理说成谬误,将谬误说成真理。
为了给巴门尼德辩护,芝诺把他的论证构造成悖论的形式,看似有一些道理实际上又是自相矛盾的。下面,我们来看看这四个悖论分别是什么。
悖论一:二分法

芝诺悖论一:二分法
芝诺:“一个人从A点走到B点,要先走完路程的1/2,再走完剩下总路程的1/2,再走完剩下的1/2……”
那么如此一来,这人是永远也无法从A走到B了。
悖论二:阿基里和乌龟赛跑
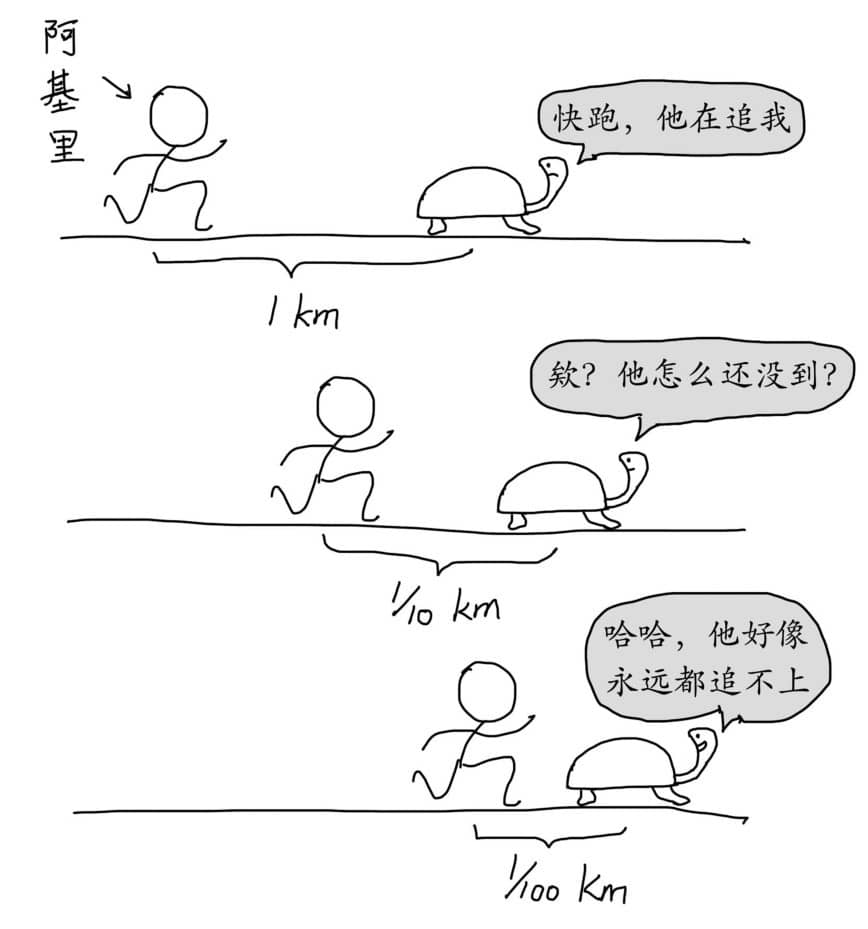
芝诺悖论二:阿基里和乌龟赛跑
古希腊跑得最快的英雄阿基里和一只乌龟进行赛跑,乌龟可以先爬一段路程,然后阿基里跑完这段路程后,乌龟也向前爬了一段路程,当阿基里跑完这段路程后,乌龟又向前爬了一段,如此一来,阿基里永远也追赶不上乌龟。也就是说一个跑得快的人,永远追赶不上一个跑得慢的人。
芝诺前两个悖论的共同点就是否定了运动的连续性。芝诺从理论上把运动分割为无数个瞬间,以为每一个瞬间就是静止不动的了,但事实并非如此。事实上运动是连续发生的,但芝诺不承认经验意义上的事实,他只接受经由理性思辨思考出来的东西。
芝诺的思路是暂时先“承认”运动,然后通过理性分析去揭示其中产生的悖论。他通过否定运动的连续性,达到否定“运动”的目的。
悖论三:飞矢不动

芝诺悖论三:飞矢不动
一支箭从A点射向B点,那么从A到B的这段路程中,每一段时间都可被分割为无数时刻,每一个时刻中,这支箭都占据一个位置,因此是静止不动的,就是说这支箭是停留在各个位置上的,而不是从一个位置飞向另一个位置。
这个论证的结果还是为了说明事物不是运动的,运动可能只是一种幻象。但芝诺却犯了一个错误,它在理论上把运动分割为无数个间断的片段,把静止绝对化,但在实际当中运动却是连续发生的,好比这支箭从A射向B是一个连续运动的过程,你不可能见到这支箭停留在A到B当中的某一个位置吧。
悖论四:一倍的时间等于一半的时间
芝诺的第四个悖论是“一倍的时间等于一半的时间”。这个就是一个纯数学游戏,是一个相对速度的概念。我们需要借助一个图形来说明。
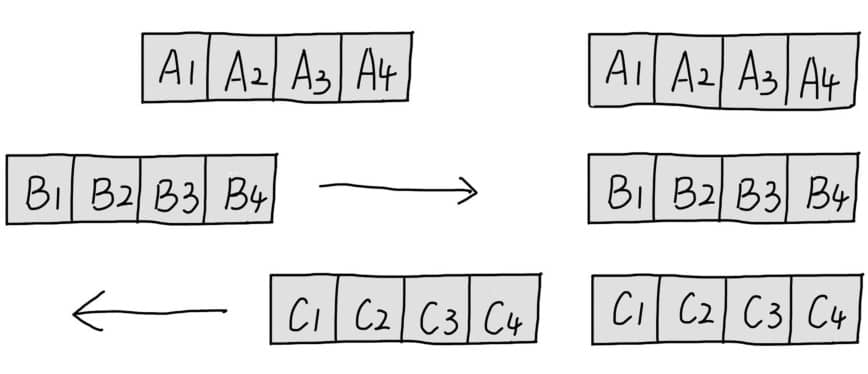
芝诺悖论四:一倍的时间等于一半的时间
假设有A、B、C三行物体,A这一行是静止不动的,B行和C行物体朝着相反的方向移动,它们的速度是一样的。
当B4达到A4时,C1也达到了A1,这两行用的时间是一样的。
在这段时间里,B4通过A行两个位置,而通过C行四个位置。
B通过C的数量要比通过A的数量多了一倍。因此B行用来越过C的时间要比它用来越过A的时间长一倍,或者说B越过A的时间是越过C的时间的一半。
但实际上B4和C1分别用来走到A4和A1的位置的时间又是相等的。
因此得出一个结论:一倍的时间等于一半的时间。
以上就是芝诺的四个悖论。
现在看来,这些太荒谬了,但对当时的希腊人来说,这些论证是非常具有迷惑性的。芝诺的论证就是为了颠倒常识,培养大家用纯粹逻辑的形式来认识世界的思维习惯,用思维真实性来否定现实中、感觉中的真实性。
他的一切论证,只为得出一个结论:否定运动的可能性,运动是不存在的,只有存在本身是不动的。这一切都是为了给巴门尼德进行辩护。
反观历史,虽然说芝诺的论证带有一定的诡辩色彩,但他的理论也蕴含着辩证法的萌芽,他重视逻辑推理论证而轻视感觉经验的做法,对于推动西方形而上学的发展又是至关重要的,我们也要承认芝诺在西方哲学史上的重要贡献。
