所有的量子力学都源于一个自然的基本性质：不能在随意精度下同时测量一个粒子的位置和动量。如果百分百确定了其位置，那么就会对其动量一无所知，反之亦然。通常会有一个折中。如果一个粒子的位置可以确定在某点周围半径r 范围内，那么它的动量至少有一个不确定度p ，满足
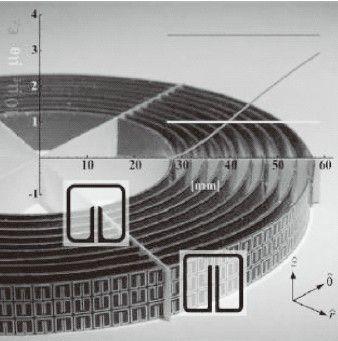
其中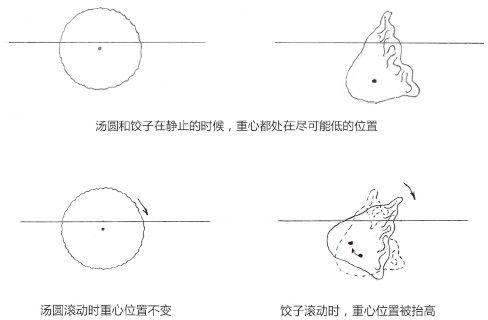
是一个自然常数，一般称为“普朗克常量”（实际上还要除以2π）。这个值(4) 非常小，所以在宏观条件下可以忽略，但是对于原子和组成原子的更底层粒子来说，它就起到了关键的控制作用。
对于时间和能量，也有相似的不确定性（上一段中我说“一个”自然的基本性质，因为在时空中，这种空间＆动量的量子跷跷板和时间＆能量相互匹配）。这意味着在非常短的时间尺度上，可以“违背”能量守恒。这里的“违背”加了引号，原因是人们不能探测到它；究其根源在于，已知时间后，人们不能精确测定能量。粒子可以辐射出能量（例如以光子的形式），只要这些能量在短时间内被其他粒子再次吸收，就似乎违背了能量守恒定律。能量账户透支得越多，那么偿还就必须越早：正如你的银行账户透支得越多，银行就可能越快地催你还款；而在截止日期前还款对双方都有利。这种对于能量守恒的“貌似”违背，在粒子之间力的传递中起到了重要作用。在电磁场的量子概念下，虚拟的光子是一种量子包或者光“粒子”，它穿过时空并在遥远物质之间进行力的传递。
请注意我是如何在这里将“光子”过渡为光的“粒子”的。光不是一种波吗？这种波粒二象性，根源可以追溯到牛顿。从光线的表现上看，它似乎是由粒子束组成：沿直线传播，能形成清晰的影子，在不同介质的交点会发生折射（比如空气和玻璃），符合经典几何光学原则。但是光也有明显的波动特性：影子的边缘实际上会产生模糊现象；当穿过几个小孔后，会互相影响从而产生明暗相间的干涉条纹。在某种特定情况下，两束重叠的光会出现消光现象，如果认为光是一种波，这种现象就很容易理解：当两个波峰相匹配时，就会形成一个更大的峰使得亮度加强，但是当波峰和波谷匹配时，两个波都会消失，出现消光现象从而形成黑暗。
1900年，马克斯·普朗克（Max Planck）发现光会以一种微观的能量“包”或者“量子”的形式发射，他称之为光子。1905年，爱因斯坦证实当光在空间中穿行时，会保持这种包的状态。在他的能量量子理论基础上，普朗克提出了著名的普朗克常量，简写为符号h ［而h /（2π）被表示为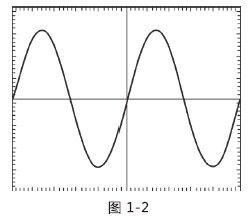
］。这就是量子理论的开端，而它的第一个成果就是成功解释了原子为何能够存活。
氢原子内部有一个电子，这个电子表面上绕着中心质子以光速的1/137旋转。以1000千米每秒的速度沿10-9 米的轨道旋转，意味着每秒旋转一千万亿圈。根据麦克斯韦理论，这时电子会极容易放射出电磁辐射，以至于当原子形成的瞬间，电子应该会立即按螺旋轨道靠近原子核并最终合为一体变成一束闪光。那么原子是如何得以存在的呢？很快人们发现，辐射能是量子化的，由此尼尔斯·玻尔（Neils Bohr）假设原子内部的电子能量也是量子化的：它们只能具有某些特定的能量。电子会被约束在这些特定的能量级中，因此不能辐射出连续的能量，所以也不会平滑地向原子核旋进。取而代之，电子只能从一个能级跃迁到另一个能级，并同时释放或吸收能量以保持总能量值不变（在大的时间尺度上能量守恒）。一旦电子到达了最低的能级，就没有更低的能级可以去跃迁了，所以它们就会保留在这个能级上，最终形成一个稳定的原子。也许你已经开始怀疑这只是信口雌黄：原子稳定因为它本身就是稳定的而已。但是，如果我们从波动性的角度来看，可能就会知道原因了。
玻尔假设普朗克常量h 决定了原子周围电子的能量级。从现代科学来看，光和电子都有波动性，波长和动量之间可以通过普朗克常量h 联系起来。将这个理论应用到氢原子：它是最简单的原子，其外围只有一个电子。当其中的电子波路径不“匹配”时，就会发生抵消而被破坏。
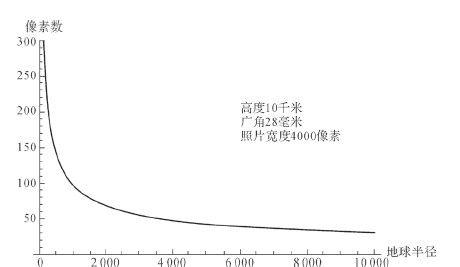
图7.1 玻尔原子模型中的电子波
图7.1对这种情况进行了解释。在（a）图中，用波的形式表示出一个移动的电子。现在，想象一个完整的波长弯曲形成一个圆圈。当波和圆圈精确匹配时，就会形成符合条件的第一种轨道；而当波不按这种情况匹配时，它就会消失。两个波长形成的圆圈如图（b）所示，这是第二种玻尔轨道，相比第一种轨道，它的能量更高，而更高的能量必然有更多的波长，从而匹配形成了图（c）这种圆周。这种简单的描述和我们已知的各种原子特性非常吻合。
当电子停留在一个轨道上时，不会辐射出能量，但是当它从高能级跃迁到低能级时就会辐射能量。玻尔假设这些辐射能都转换成了光，然后计算对应的波长，结果发现其与氢原子的复杂光谱完全吻合。爱因斯坦后来又将普朗克的量子理论成功地运用到了光子的辐射问题上。普朗克量子理论以及玻尔的重大发现，对于当今的科学影响深远。
其中一个重要的影响就是，量子理论认为所有的物质都具有波粒二象性：我们通常认为电子是一种粒子，但事实上它是“电子场”的一个量子包，具有波动特性。也许这听起来不可思议，但确实如此；根据电子的波动性，人们才发明了电子显微镜。
这些波是什么？怎么才能和之前的测不准原理联系起来？这些问题从量子理论出现开始，就一直困扰着科学家们。爱因斯坦和玻尔代表着两派，长期就量子理论的含义争论不休，所以我个人对此也不敢妄下结论。这里我只想将它们罗列出来；如果你倾向于其他的观点，那么请你继续，因为现在还没有一种共识，也没有一种“正式”的解释。
在最单纯的情况下，我们只需要接受测不准原理以及相应的推论即可。但是，如果我们能够在脑海中形成一个模型，其具有上述理论中的所有性质，那就更好了。我们就可以通过直觉对其特征和含义进行推广。位置和动量的测不准和我们熟悉的一种情况非常类似。首先，画很多的点形成一个固定波长的波形；接着，我们将位置等同于波形上的一个固定的点的坐标，而动量等同于波长；这就和测不准原理的工作方式很类似了。根据量子力学，动量越大波长越短。假设我们知道准确的位置，那么我们就只能画一个单独的点，而不可能知道波长是多少；波长可能是任意的。如果我们画了波形初期的几个点，那么就可以初步判断波长是短还是长，而只有画完－整个波长，才能知道波长的准确值。但是，当我们确定了波长后，位置确定的最高精度也不可能高于波长长度了(5) 。
可能你会发现，在定义波的位置的时候有些矛盾；只有当测定完了整个波长之后，才能确定一个波。如果这个矛盾让某人突然开窍，开始接受存在一个熟悉的概念，即位置和另外一个值不可能同时被准确地定义，那么这个人一定会开始感激量子世界的自然馈赠。由于波具有这些特性，因此人们在对思维模型进行构建时需要非常小心。然而在我看来，他们还仅仅停留在思维模型的程度上。
