通过对电磁辐射、光等进行思维实验，爱因斯坦创立了他的狭义相对论。顺着这个路子，他开始思考万有引力，最终提出了广义相对论。
爱因斯坦最初的狭义相对论基于一个假设，即没有绝对的静止。而他的广义相对论同样基于一个假设，即没有绝对尺度的力和加速度。他首先考虑包含引力的相对论问题。光速是一个广泛的常数，这是一个公理，也是狭义相对论的基础。光具有能量，而引力不但会作用于质量而且还会作用于各种形式的能量，所以引力会弯曲光束。当光束经过比如太阳这种巨大的物质旁边的时候，这种弯曲就会非常明显。由于在宇宙中引力无处不在，所以光束总是会被扰乱。所以相对论原理中提到的基本假设，即光沿直线匀速传播，看来不可能实现，除非有什么办法能将宇宙中的引力关掉。爱因斯坦意识到这是一个迫切的问题，而要彻底解决它需要花费自己十年光阴。而当他想到自由下落的物体时，突然意识到此时引力实际上就被关掉了。这个想法非常重要，意味着此时没有净力作用在物体上，因此它在做匀速运动。
一块下落的岩石是没有质量的。如果你接住它，所感觉到的质量实际上是一个力，用于阻止石头落地。我们脚下坚固的地板阻止了我们下落到地心中去。地板给了我们一个阻力，阻止我们掉下去，这个阻力就是我们平时感觉到的质量。倘若地板和地球都是蒸汽，那么我们就会失重，最终掉落到这颗美丽行星的中心里去。
以此为出发点，爱因斯坦进行了另一个思维实验。
假设你处在一个自由下落的客舱里，客舱没有窗户，因此你无从知晓外面的情况。也许这个客舱是一个故障电梯，或者是没那么恐怖的绕地球飞行的卫星。在卫星的例子中，你和卫星都在自由下落，但是却一直在“水平”运动，地球表面的弯曲使得地表在远离你的同时，你也在按相同速率朝它掉落过去。而在电梯的例子中，在你可见的周围你无法感觉到任何万有引力。比如，如果你松开手里的球，它会受到地球引力，最终和你按相同速率朝地心飞去，结果相对你而言它是静止的。而宇航员之所以能在飞船中悬浮，也是因为他们和飞船在以相同的速率“掉落”。虽然我们有幸知道宇航员们是在地球重力场作用中下落，但是宇航员自己却感觉不到力，在飞船内封闭环境中他们完全可以认为自己是静止不动的。爱因斯坦认识到，在自由下落的“失重”状态下，实际的地球引力已经消失无踪了。
这同样适用于光束。光和常规的实物一样，会被巨大的物体所吸引。1919年发生日全食时人们就证实了这一点。当日全食发生时，遥远的恒星偏离了人们眼中的“正常”位置，因为当这些恒星发出的光经过太阳附近时被太阳引力场弯曲了。(1) 假设你被关在一个自由下落的客舱中，然后与客舱地板平行地打开一束手电筒光，同时在地面进行精确的测量，会测到这束光随着引力“下落”时发生了略微的弯曲。在光从客舱的一端飞向另一端的过程中，它会和对面的舱壁按相同速率跌向地球。最终导致在客舱内部看来，光是按直线传播的；并且再一次地，所有现象都显示你确实在一个不受力的自由环境中处于静止状态。
假设你所在的飞船隶属一个太空舰队，舰队中每艘飞船都精确地按1千米的间隔排开，保持队形朝地球自由下落。此时所有的宇航员都会觉得自己处于静止状态，或者在平行直线上运动，但很快他们会注意到所有的飞船正在互相靠近。产生这个现象的原因是，每艘船都在向远处的地心自由下落，而相对地心点的轨道会不断收缩。爱因斯坦的观点认为，引力的作用使得自由下落物体的轨迹会汇成一点。
地球南北极附近的经度线也会汇集，这与上述画面很像，这个相似的情形使得爱因斯坦得出了一个深奥的见解。如果在一个平表面绘制地图，比如作墨卡托投影，经度线会相互平行；而在地表的曲面上，这些“直线”最初在赤道上是平行的，但随着一端朝北延伸，这些线开始渐渐收缩并最终汇聚到极点。究其原因，是二维的地球表面被弯曲到了三维。由此，爱因斯坦作出了一个重大的推论：在引力场作用下，自由下落的线和某个“面”上的经度线相似，会在某些更高的维度下发生弯曲。他想象空间的三维“面”会被巨大的质量团所拉伸。而沿着这些曲线的自由落体运动，被觉得是偏离了“直”线，并被归结成是万有引力的作用。
想要理解爱因斯坦是如何将这个想法与其时空理念结合起来的，我们可以先看看二维的例子。首先回想一下毕达哥拉斯定理，直角三角形的斜边长的平方等于两个直角边长的平方和：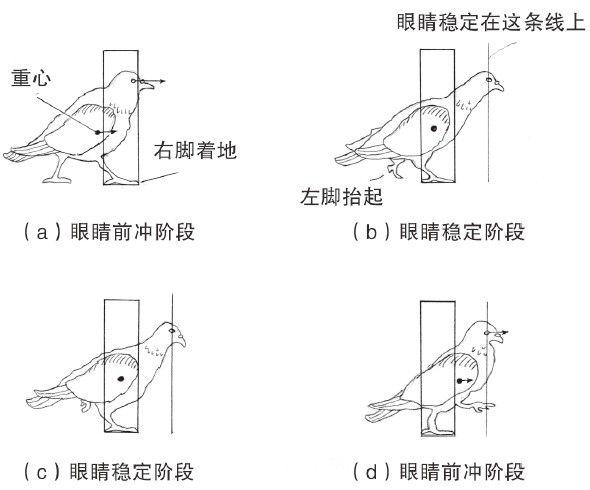
。在平面上，三角形的3个角度和为180°，上述定理成立；而在曲面上，这个定理是不成立的。如果我们想象一下环球旅行，这就更容易理解了。我们首先沿着赤道前进，由本初子午线走到东经90°。然后，向左转90°，向北走到北极点。然后再向左转90°，会朝向南方（从北极点看，所有方向都是南方）。之后你会沿着本初子午线向下走，最终到达赤道上的起点，这样就完成了一次三角形的旅行，而这个三角形有3个直角。显然，这3个角度和超过了180°，这就已经表明你不是在一个平整空间中；而很明显地，这不适用毕达哥拉斯定理－－这里哪条边是斜边呢？
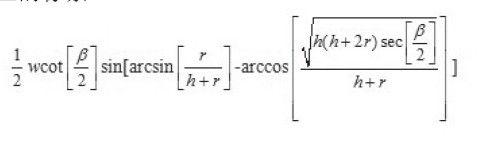
图6.1 所示为一支手电筒处于自由下落的盒子中部。它发出的光穿过盒子，地心引力作用将盒子和光束同时拉向地面。在（a）图中，显示从地面看几个纳秒内出现的弯曲光路。在（b）图中，显示在盒子内部的人感觉到的光路。由于盒子和光都按相同速率下落，光在盒子内部呈现水平直线穿行状态。
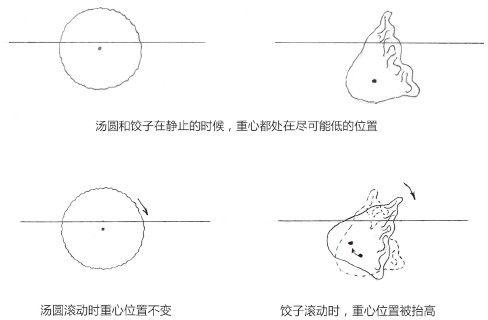
图6.2 叠加了一个三角形的地球模型。三角形的一条边由赤道开始，沿着本初子午线到达北极点；底边沿着赤道，从本初子午线开始，到东经（或西经）90°为止；第三条边从赤道开始，沿着东经（或西经）90°线到达北极点为止。
居住在弯曲面上还有很多其他的惊奇之处，比如：当所有的线都会在至少一个维度上产生弯曲，那什么才是直线呢？
在平面上，两点之间的最近距离就是一条直线。爱因斯坦意识到，最短距离的概念是基本；在被引力扭曲的时空中，光会沿着两点间最近的路径飞行。在地球表面，最近的路径就是圆弧。从北纬55°的伦敦飞到约北纬30°的洛杉矶，你可能天真地以为朝向西南方飞行更近，而实际上航班会沿着西北方向的圆弧飞行，跨过格陵兰岛。这种圆弧正式的名称是测地线，意思是“地球分隔线”。这种情况下的三角形，各边长的关系公式就比毕达哥拉斯定理复杂多了，必须给出表面的弯曲情况、相对各个角的“米”长是多少－－专业术语称为“度量”标准。爱因斯坦要建立扭曲时空下的引力理论，需要回答两个问题：①在物质的一些结构中，时空度量是什么？②在度量的形式下，物体如何四处运动？
如果没有物质，我们可以使用已有的度量标准公式：
，且时空被认为是平的。而当物质出现之后，距离和时间的关系就会发生变化，时空就发生了扭曲。
在我们的太阳系中，最著名的时空弯曲证据来自水星。和其他行星一样，水星的运转轨道也是一个椭圆，但是其近日点在发生明显的进动。在到达近日点时，它离太阳最近，受到的万有引力最强，运动得也最快，也最容易受到相对论效应的影响。空间弯曲使得太阳周围的距离发生了轻微改变，变得和平展空间内牛顿体系的值不同了。在牛顿体系内，物体完成一次绕圈之后，会在相同的轨道重复运动；但空间弯曲时，物体每次的运转轨道都不会完全相同。最终导致的结果是，水星的运转轨道每年都在变化，这完全印证了爱因斯坦的理论。
图6.3 水星近日点的移动。图上所标出的1、2、3点表示在相继的三个轨道上的离太阳最近的点。
爱因斯坦认为，时空就像一种弹性固体，比如一张橡胶板。此时，当一个巨大质量块出现在介质中，比如太阳或者地球，就会产生一个很大的引力导致介质发生弯曲。如果这个质量块在加速，比如两个恒星相互旋转，或是一颗恒星突然瓦解然后爆炸成一颗超新星，根据爱因斯坦的上述理论，此时就会向媒介中发射引力波，就像地震会向地球中发射地震波一样。
关于引力辐射的发生，现在仍然只是一个预言，亟待实验验证，直接办法是如何实际测到这种波。但所幸已经有间接证据支持这个预言。有两个恒星，名为脉冲双星PSR 1913＋16，它们按7小时45分钟的周期相互旋转。此脉冲星每1/600秒会发射一次脉冲电磁波，就像灯塔发出的旋转灯信号。当灯塔的旋转光束指向你时，你才会看到一次灯塔闪光，而当它转到其他方向上时，你就看不到。而脉冲星发出的两个连续脉冲之间有1/600秒的时间间隔，这意味着脉冲星每秒旋转17次。在爱因斯坦的理论中，这种双星系统会以引力波的形式放出能量，而其轨道周期会缓慢变短。天文学家约瑟夫·泰勒（Joseph Taylor）和拉塞尔·赫尔斯（Russell Hulse）后来测到了这种周期变化，并发现其与爱因斯坦的预期完全吻合。由此他们获得了1975年的诺贝尔奖。
有了爱因斯坦理论的这个证据，我们开始相信空间确实类似一种弹性介质，这不禁让人联想到爱因斯坦研究电磁辐射时用过的以太，而他的狭义相对论早就将以太论击得粉碎。尽管如此，相对论中并不意味着不存在以太，只是说在那种以太中的物质必须符合相对论原则！“以太”的一个例子就是电场，你通常无法发现它，除非使它发生振荡：此时就会发现它确实存在。相对论下的以太同时需要电场和磁场，其中的转换会按光速传播。类似地，对于引力场以太，在时空度量下荡漾的引力波也会按照光的宇宙速度传播。
