如果说以太定义了绝对空间，那么我们相对于以太的运动速度是多快呢？要得到这个问题的答案，麦克斯韦对电磁波速度的计算是一种解释途径。要说明这点，首先考虑一下水波。我们扔一粒石子到水中，水波就会产生并扩散开去。水波的速度约1米每秒。这个速度是水本身的一种性质，与振动源的速度无关。无论石头是从静止的船还是高速前行的船上扔下，形成的水波速度都是1米每秒。如果你站在静止的船上，会看到水波以1米每秒的速度离你而去。但是如果船朝着波源以10米每秒的速度进发，你会看到波以11米每秒的速度向你袭来；相反，如果船以10米每秒的速度驶离波源，那么你会以9米每秒的速度摆脱水波。通过这个方法，你就能确定自己相对于水的所谓绝对速度。
沉浸在以太中的地球与水中的船类似。电磁波的移动速度为300000千米每秒，这是宇宙的性质，与波源的速度无关。这一点和水波完全一样。与前面的方法类似，如果我们在以太中运动，通过测量看到的光波速度就能确定我们相对于介质的绝对速度。这个实验只需要测量光在不同方向上传过以太的速度，据此就能够找到与麦克斯韦的计算值完全匹配的构架。而这种构架就是宇宙的基本构架：相对于以太而言完全静止的一种状态。
牛顿运动定律在这里似乎完全适用，甚至是无可替代的。即如果地球在相对以太做运动，那么以相同方向运动的光就会被地球速度所加速，而与之垂直运动的光却不会有加速现象。根据麦克斯韦的理论计算，只有在相对以太完全静止时，光速才会是300000千米每秒。
地球距太阳1.5亿千米，因此地球公转一圈要走数十亿千米的路程。考虑公转周期是一年，约3千万秒，这意味着地球公转速度约为30千米每秒。根据麦克斯韦的理论，光“相对以太”以300000千米每秒的速度运动，那么当地球运动到公转轨道上以圆心对称的两点上时，其相对光的速度会有60千米每秒的不同，即光速的1/5000。
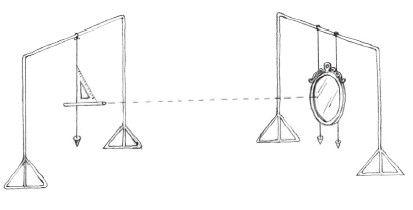
要测量由地球运动引起的如此微小的光速变化，需要很精密的仪器。艾伯特·迈克逊（Albert Michelson）在1881年进行了首次实验尝试。但直到1887年，他才通过与爱德华·莫利（Edward Morley）的合作达到了测量所需精度。在他们的方法中，并不是比较相隔半年的同一个实验的不同结果，而是只进行了一次实验。他们将一束光一分为二，然后向不同方向发射，最终通过镜面系统将其折回起点。两束光的发射方向相互垂直，因此，如果一束光与地球运动方向平行，另一束则会垂直于地球运动方向。两束光会以不同的方式受到以太的影响，所以当他们经过折射回到起点时，到达的时间会略有不同。而两束光的振荡频率相同，那么这种到达时间上的微小差异会体现为振荡幅度的不同。
如果一束光波速度变慢，譬如以太影响了它的速度，那么它的振荡时间就会比另一束略长，两束光的波峰和波谷会干涉形成明暗相间的条纹。通过测量条纹的宽度和数量，就可以精确地标定出两条相互垂直的光束之间的相对速度。最初迈克逊在柏林独自进行这个实验，之后又与莫利在美国合作进行了更高精度的实验。但自始至终，期望的明暗相间条纹都没出现，他们因此推断：地球没有在以太中移动。迈克逊说得更为直白：静止以太的假设是错误的。
从逻辑上说，这个结论无懈可击；其意义巨大，立即引起了许多猜想。其中一些猜想认为以太就像皇帝的新装，也许存在，但是只有智者才能看见，俗人是无缘得见的。在皇帝新装的故事中，所有人都声称自己看到了皇帝华丽的衣服，直到一个天真无邪的小孩给出了正确的回答：皇帝一丝不挂，根本没有什么新装。与之类似，其实根本不存在以太。之后的爱因斯坦理论也完全证明了这一点。当然也有人认为，地球通过摩擦力将以太拖带着一起运动。地球在以太中移动，带起了一个巨大的以太漩涡，以至于虽然地球相对遥远的以太是运动的，但是相对周围的以太来说却是静止的。
牛顿很早就发现，物体即使在空气中运动也会受到阻力。要达到他的运动定律所需的基本条件，即永恒不变的运动状态，必须将这种阻碍移除。因此以太也必须绝对消失才行。比如，牛顿运动定律可以对行星的运动进行准确描述，这意味着行星在太阳引力作用下自由地运动，没有受到什么阻碍。以太自然就没有和行星发生任何反应。但是这立即出现了一个悖论，即如果地球能将周围的以太拖动，那么必然就发生了相互作用，自然牛顿力学对行星运动的描述就不可能成功。尽管如此，仍出现了很多极富想象力的猜想。乔治·斯托克斯（George Stokes，1819－1903）是一位英国物理学家，以研究黏性流体闻名。他接受光的波动理论，也相信以太的存在。他认为，以太和蜡类似，虽然坚硬但是在力的驱使之下也能流动。这进而引出一些观点，认为行星的运动加载了一些力使以太流动起来，或者行星也通过摩擦力将以太拖着随自己运动。不幸的是，从来没有找到实验证据能证明这些观点。最终，这些猜想都因为各种特定性而被历史的洪流否定掉了。
英国的乔治·菲茨杰拉德（George Fitzgerald）和荷兰的亨德里克·洛伦兹（Hendrik Lorentz）发现了第三种可能的解释。他们各自独立地注意到，如果物体穿过一个以太，在运动方向上会发生收缩，收缩量决定于其对地球速度与光速之比的平方。如此，物体在以太中的运动就会被掩蔽而不被发现，迈克逊和莫利的实验结果也得到了很好的解释。
这个观点的细节如下。假设有一把米尺静止在地面上，现在想象一下这把尺子快速地在你面前飞过，当然这一切都发生在以太中。洛伦兹和菲茨杰拉德在当时给出了一个假设（现在知道这个假设是正确的），即使电磁力将尺子这种固体聚拢在一起，而在以太中的穿行会打乱这些力。他们利用麦克斯韦理论进行了计算，当物体运动速度为v ，光速为c 时，尺子的长度会缩小一个微小的量：
地球的速度为30千米每秒，通过计算知道缩短量会小于百万分之一：一米长的尺子会缩短约一微米。
这个理论认为，当指向以太时，迈克逊和莫利实验中所用的设备会缩短；而与以太垂直时，长度则不变。这种纵向收缩和横向不变引起的距离上的微小差距，与期望的两束光之间前后到达的时间延迟完全吻合，最终导致无法测到光程差。在这种解释下，以太可以填满空间，而以太中的运动本身就不可能被测到，根源在于测量装置本身就会帮忙将结果隐藏起来。
这种解释也意味着物体在以太中运动时，对于加速度的反应会发生变化，即运动物体的惯性或者说质量会按
增加。因此，随着物体的速度v 接近光速c ，直到v ＝c ，此时物质的质量会变得无穷大。所以无论多轻的物体，要将其加速到光速，所需的力都是无穷大的。这种观点似乎有点牵强，当时并不广为接受。但在1901年，科学家发现放射性β射线中的电子运动速度不同时，质量也不相同，而质量与速度的关系完全符合以上公式。这使得人们开始关注洛伦兹-菲茨杰拉德变换，其也开始被大众逐渐接受。
今天人们知道这些速度相关的变换是正确的。随着速度增大，长度会压缩而质量会增大。参考的变换公式就是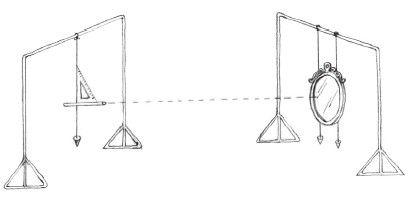
，但这种变化的原因并非如洛伦兹和菲茨杰拉德所言。关于这个问题，爱因斯坦有一个新观点：无论光源或观察者的速度如何，光速都不变，这种现象在某种程度上是因为传播距离按洛伦兹-菲茨杰拉德公式在缩短，而这种缩短并非源于以太对于尺度的作用。对于爱因斯坦而言，收缩是空间本身的一种固有性质。不同速度的观察者记录距离和时差的方式是不同的：一个观察者眼里的空间对于另一个观察者而言却是一个时空混合体。这个观点是爱因斯坦相对论的基础，其开创了一个全新的时空观。
