挤出来的沐浴露为何打圈圈?
引子:
在Dr. Who1的生活中,肥皂已经越来越少地出现了。取而代之的是洗手液、洗面奶、洗发水、护发素、沐浴露……各种瓶瓶罐罐。而这些清洁用品,不管是倒出来、挤出来,还是压出来,都有一个共同的特征,那就是:打圈圈。 【1Dr. Who是D r.Yo u栏目搜集来的问题发问者】
问:为什么倒沐浴露之类的黏稠液体时,原本垂直下落的“液体柱”会出现“旋转堆积”的现象?
(科学松鼠会论坛 乌子虚2)【2出现的此类人名皆为科学松鼠会成员或热心读者的网络ID。】

“Ziplb”的热闹答案
其实这是一种低雷诺数流动的典型现象,雷诺数即流体惯性力与黏性力之比,雷诺数越小,流体中黏性力的作用也就越大。在倒洗发水等高黏性的流体时,由于黏性力的作用,每部分流体微团都会受到相邻流体微团的“拉扯”与“牵制”作用,在靠近地面堆积时,自然也会受到已堆积流体的“拉扯”作用,而惯性力无法抵消这种黏性力的作用,“拉扯”的合力形成了“旋转堆积”的现象。这样就容易理解,倒水的时候不会出现这种现象了,因为此时为高雷诺数流动,流体惯性力的作用大于黏性力的作用,足够抵消已到达地面流体的“拉扯”,故流体流下时沿惯性力的方向垂直下落。
用水、米汤、菜油、洗发水、牙膏、沥青依次倒来看看,你会看到“旋转堆积”从无到有的渐变。当然,前提是征求了你老妈的同意。
当Dr. Who的朋友乌子虚提出这个问题的时候,也许谁都没有意识到松鼠和他们的朋友们将经历一次有趣的穿越之旅。问题被公布之后,散布在世界各地的松鼠们都出动了:有的将库存的蜂蜜缓缓倒向餐碟;有的躲进洗手间将洗发水挤向洗手池;有的借口要做炸全鸡,把油瓶里剩下的食用油全倒进了锅里;还有人低下头,让唾沫拉出一条长长的轨迹……八爪鱼最先公布了自己的伟大发现,在把剩下的香波都倒进了洗手池之后,他观察到了五次方向相同的螺旋堆积。在科学松鼠会的聊天群里,他兴奋地告诉大家,这个现象首先是肯定存在的,并且能排除人为的因素,同时向其他的松鼠求证各自的螺旋堆积是不是也有方向性。当时Robot正在南半球的某图书馆学习,看到八爪鱼的实验结果,放下书冲进洗手间,一次又一次挤压洗手液,观察其下落过程中的形态以及方向。很快,图书馆的保安注意到了这只形迹可疑的松鼠……很快,Robot下线了,过了很长很长时间,Robot又上线了,她告诉大家,经过自己在家反复实验,证实香波的确能形成螺旋堆积,但是没有方向性。我们问她为什么刚才还在图书馆,现在变成在家,她支支吾吾地说:“洗一个香波澡,是南半球最舒服的事情。”我们愤愤不平地讨伐起了Robot所在学校图书馆的保安,此时瘦驼却不声不响发来了他拍摄到的漂亮螺旋堆积,Fwjmath随后给大家提供了一段清晰的视频。八爪鱼看了看瘦驼的图片,看了看Fwjmath的视频,最后看着自己拍的图片,缓缓吟道:“禅心似月迥无尘啊……”与此同时,热情的网友们纷纷发来了自己对这种现象的观察以及解释,观点不尽相同,但,那个星期里,咱们国家的香波消耗的确达到了一个历史高峰。
我们为拉动内需作出了重要的贡献!

From“八爪鱼”
这个世界,有时候就像是堆积的香波,旋转往复。50多年前,有两个和乌子虚同学一样对科学和生活都充满着热情的美国人,G.Barnes和R. Woodcock,他们也注意到生活中这个有趣的现象,并且第一次针对这种现象进行了细致的观察和分析,以此撰写了一篇论文。当我看到发表于1958年的这篇论文时,不禁会心一笑。他们没有什么高级的仪器,也没有作复杂的数学分析,只使用简单的摄影工具,用大头针对螺旋的尺寸进行比较分析……
从那时起,这种现象有了自己的名字:Rope Coiling Effect,中文译做“卷绳效应”。在那之后,越来越多、越来越专业的学者,投入到这种卷绳效应的研究中去。研究者孜孜不倦地探索这种现象的成因,黏稠度、高度、直径、重力、气流、媒质……各种能产生影响的因素陆续得以确定。
在我们日常生活中,经常能观察到流淌的液体。打开洗碗池的水龙头,自来水流出后会撞击池子底部,迅速铺散成一个平面。但如果流出的是香波之类的液体,情况却会有些不同。
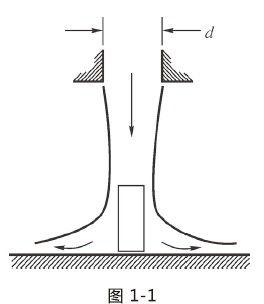
图1-1描述的是流体流到平面上铺散的情形。像水这种黏度很小的液休,因为水分子之间吸引力很小,铺散过程非常迅速。但是比水黏稠许多的液体,分子之间吸引力较大,铺散的过程就会慢一些。这导致液体还来不及向四周流溢,新的液体柱又流了下来。这样就会有一部分液体图 1-1堆积在一起,形成一个类似圆柱的结构。
很明显,这个液体的圆柱结构不是静态的:虽然底层以及最外层的液体会不断流失,看起来像是坍塌一样,但上方不断有新的液体流下来补充,于是圆柱形的累积液柱在动态中得以保持。液体圆柱内部分子之间的引力,对抗圆柱本身的重力以及惯性,如果两者之间的力能保持平衡,液体圆柱的形态就会出现表观上的平稳。所以当我们开始向手上倾倒香波的时候,它呈现出静静流淌的样子。不过当我们将香波瓶子提高点,让香波从更高处流出,情况就有了变化。整个液流的长度增加,由于重力加速度,越到下方,液体的直径越小,速度越大。
显然,这时,中心的圆柱受到来自重力以及惯性的压力在增加,而圆柱的直径在减小。一旦圆柱的分子间引力不足以平衡重力及惯性,这根柱子就会坍塌。一根不堪重负的柱子,会怎样?两端所受到的压力,将使得这根柱子产生形变,同时,内部分子之间的距离变短。在垂直方向上,分子之间因为距离缩短,表现为相互抗拒,并积蓄势能。如果这根柱子内部的分子,是完全一样的,那么柱子的任意水平切面上,所有的分子受力情况都相同,这根柱子就会出现压缩变形(crushing)。此外还会有什么情况呢?肯定有同学玩过叠木块,在这个游戏中,两个玩家依次从木塔中部取出一个木块,最后谁抽木块时导致木塔的倒塌,谁就是输家。我举这个例子是为了说明,整个木塔的重心,保持在中心纵轴上,在某水平切面上,如果和中心纵轴等距离的某处的受力与其他对称位置的受力相比,出现足够大的差异,木塔的重心偏离中心纵轴,木塔就会倒塌。刚性材料受力过程中发生的折弯(buckling),和这种现象有共通之处。
为什么柱子受力会发生压缩,而一根杆子却会“弯下了腰”呢?这是因为如果杆内部物质分布足够均匀,使得内部力的分布足够均衡,材料本身的形态也对称,则只会发生压缩,不会发生折弯。但自然界的物质,几乎没有完全均质的。
折弯也并不必然会发生,只有当材料的长度和直径之比达到某一水平,或者材料内部物质分布的不均匀程度达到一个所需水平时,应力在中部集中,其受力分布的异常程度能克服材料边界的限制,突破边界的折弯才会发生。
如前所述,流体的液柱是由一个动态的平衡过程来保持其形态稳定的。在物质不断更换的过程里,总会有局部的异常形态出现。有时候是一个气泡,有时候是一个密度较小的团块,
有时候是别的什么。这种内在的异常,破坏了液体内部分子间的引力和液柱重力以及惯性之间的平衡。当这种不平衡的状态,严重到一定的程度时,就会导致折弯的发生。原本处于压
缩状态下的某部分物质,受到侧方向的推挤,向阻力最小的方向释放势能,先加速后减速远离中心轴,随着离开中轴越来越远,分子间的压力渐渐转变成分子间的拉力,这股力量同时也作用在即将落下的液体上。在重力和惯性协同作用下,液柱向反方向开始新一轮的弯折。最下层的液柱,在往复过程中,内部分子在“受压—牵拉”两种状态之间来回转换,形成振动。
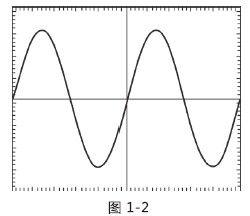
表现为在原位的往复打圈。如果以时间为横轴,振幅为纵轴的话,就会形成图1-2所示的波动。
我们先看看这个过程发生在一个平面上时的情形:一股扁平的液柱流淌下来,在横轴方向上,尽管有内部的不均衡存在,但是这种不均衡无法突破较宽的边界限制,更多地表现为压缩形变;而在纵轴方向上,内部不均衡易于突破较窄的边界限制,表现为弯折,形成振动。
正像我们前面说到的,尽管上面实验中横轴具有较宽的边界,但这个障碍也是相对的。一旦液体的黏度足够大,下落的距离足够高,即使是这样的宽度,仍然会形成弯折,产生振动。
当我们将液柱的扁平形态变成最常见的圆柱形,所观察到的过程将不限于一个平面内,变得有点复杂,但是本质保持不变。黏液下落过程中形成的液柱内部因为局部的不均衡受力,导致液柱向某一个方向弯折,形成最初的振动。此振动是在某一个平面内产生的,但在和这个平面垂直的方向看,则没有振动发生,只发生了压缩形变,就像在图1-3左边图片中所看到的。在这个平面上,一旦有新的因素,诱发折弯,就会出现另外一个波动。
如图1-3右边图所示,两者所在的平面相互垂直。前后两种振动叠加,形成三维振动。
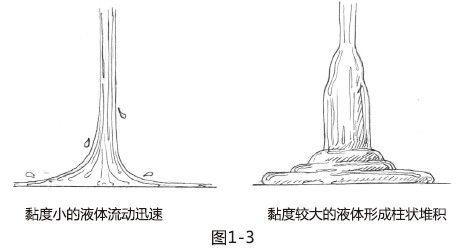
在实际中,这两个过程并无法如此截然地分开,两黏度小的液体流动迅速图1-3黏度较大的液体形成柱状堆积个平面内的振动,一起影响这条液柱的运动形态。各自条件不同,两个振动的振幅、频率也不同,产生出来的综合形态也不同。
因此在平面上产生的堆积形变可表现为单纯的折叠,也可表现为花瓣形,或可表现为8字形。
当两个平面内的振幅以及频率趋于一致时,堆积则表现为螺旋状,卷绳效应产生。
最后说一下,在过去50多年里,陆续出现了大量针对卷绳效应的论文。现在,这种现象中大部分决定性因素已经得以厘清。效应的频率、振幅、卷绳的直径、黏液的边界高度、边界黏稠度以及螺旋堆积能达到的高度,都被计算出来了,也不断有新的影响因素被考虑进来。这个研究正向着更全面、更精细的方向继续前进。

尾声:
此解答在Fujia、桔子、Fwjmath、Robot、瘦驼以及猛犸的帮助下完成。当我结束这篇稿子时,窗外一只松鼠从树枝跳上横穿街道的电线,在我的注视下摇头摆尾走过阳台。一股清风拂面而过,满是春天的味道。这一刻我突然觉得“松鼠”二字,不仅是自然界某种活泼的精灵,或是互联网上一群意气相投的人,更代表着一种对科学、对生活最简单的热情。
