我们是在地“球”上吗?
引子:
在航海大发现的年代,受技术条件所限,人们只能通过航海来实证地球是圆的。
随着科技不断发展,现在我们可以用各种复杂的仪器,计算地球半径精确到小数点后n位。可是,如果不用这些高科技手段呢?

问:
如何用便宜的设备验证地球是圆的?
“Aqdd”的热闹答案
古代中国人相信“天圆地方”,不过时至今日应该不会有人再相信这样的说法了,哪怕是随便问一个小学生,他都会告诉你:地球是圆的。这似乎已经成了一个无需证明也无可辩驳的事实,可是几千年来人类对地球形状的认知却是经历了一段相当漫长而艰难的过程。
最先提出“地球是个球形”这一观点的是生活在公元前6世纪的古希腊哲学家毕达哥拉斯。不过,他之所以持有这种信念并非源于某种客观事实,仅是因为他觉得圆球在所有几何形体中最完美。后来,亚里士多德给出了“地球是个球形”的第一个科学证据:月食时月面出现的地影是圆形的。公元前3世纪,古希腊天文学家埃拉托斯特尼(Eratosthenes)根据正午射向地球的太阳光和两个观测地之间的距离,第一次算出地球的周长。公元2世纪初,我国东汉天文学家张衡也提出了“浑天如鸡子(鸡蛋),地如子中黄(蛋黄)”的说法。公元726年,唐代天文学家一行和尚主持了中国历史上第一次大规模的官方组织的天文和大地测量活动,并利用北极高度和夏日日长计算出了子午线1度的弧长和地球的周长。但是直到16世纪初,葡萄牙探险家麦哲伦环球航海的伟大壮举,人类才第一次用实证的方法无可辩驳地证明了地球是球形的。
在麦哲伦的船队离开西班牙塞维利亚港时,当他看着港口那高耸的灯塔逐渐消失在海平面以下时,不知他是否思考过一个问题:如果大地是平的,那大海也应该是个平面,而且海上没有东西,这样不管麦哲伦的船队航行多远,只要一回头,他就必定能看到出发港口那明亮的灯塔(图5-1上图)。从理论上说,他甚至可以看到远方任一方向上的海岸。然而事实却不是这样,随着船队离开港口,船上的人们回望港口时会发现,灯塔不但越来越小,位置也会越来越低,直到完全消失在海平面以下。
任何能阻隔视线的人们的视线完全被凸出来的海面所遮挡,那些原本高出海面的陆地、港口、灯塔统统都看不见了,视线所及到处都是茫茫一片大海(如图5-1下图所示)。仅凭这一点麦哲伦先生在他开始环球航海的第一天其实就可以确定无疑地认识到地球原来真的是个“球”。
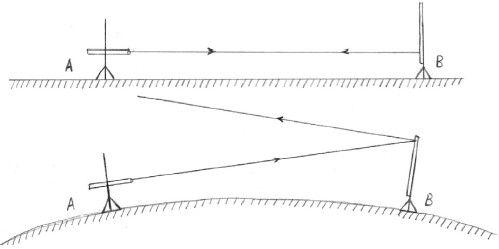
图5-1
科学技术发展到现在,我们可以通过很多方法来证明地球是个球形。我们甚至可以坐上宇宙飞船到外太空看看我们的地球家园,或者像麦哲伦一样做一次环球旅行(现在我们可以坐飞机而不必坐船)。不过既然Dr.Who让我们用比较便宜的方法去证明,那我们就要开动脑筋好好想想了。观察月食、测量日影之类的方法虽然不用花什么钱,但都被前人用过,了无新意。我倒是想到了另外一种方法,至少在我查阅过的资料里还从没看见有人用过同样的方法来证明地球是个球形。
这个实验并不复杂,开销不大,原理也很简单,只要具备基本的物理和几何知识都能看懂并理解。这个实验需要一支激光笔、一面质量较好的镜子、一把直角尺、一些尼龙丝线、三个铅锤(可用铁块等重物代替),还需要一些角铁和铁丝来制作支架。我大概算了一下,总花费也就是100元左右吧。
下面我就来具体讲解一下我的这个实验设计:
如图5-2所示,实验用具由两个支架组成,其中左边支架上有一条尼龙丝线和一个铅锤,它们共同组成了一个标准铅垂线。铅垂线上固定了一支激光笔,就是多媒体教室里老师用的那种,在玩具店也能买到类似的东西。激光有个很好的特点就是发散性小,你把激光打到一个很远的物体上,它所产生的光点依然很小且清晰可辨。激光的准直性非常好,其光线可以看成一条直线。
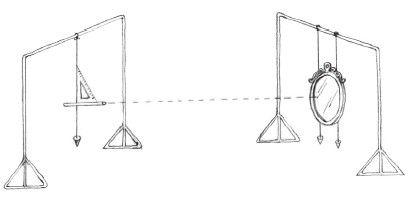
图 5-2
我们就是利用激光的这些特性来完成实验的,所以一定要买一只质量很好的激光笔,这点很重要。图中黑色的部分当然就是支架了,而那个白色的三角形物体是一把直角尺,它的作用是让激光笔,准确地说是让激光光束处在精确的水平状态。右边支架和左边支架类似,只是用了两根铅垂线,灰色的椭圆形物体代表镜子。这面镜子固定在铅垂线上使其完全垂直于水平面。用两根铅垂线没有什么特殊的目的,只是让镜子不会来回转动,你也可以用镜子代替铅锤直接吊在尼龙丝线上,让镜子本身变成铅垂线的一部分。具体怎么制作并不重要,重要的是让镜子垂直于水平面。
接下来我解释一下这个实验的目的。由于地球引力的存在,铅垂线都垂直指向地面,在我们的肉眼看来似乎都相互平行,建筑工人甚至用两根铅垂线来测量楼房上下是否等宽,这在精度要求不是很高的测量中是可行的,但从原理上讲,其实没有任何两根铅垂线之间是绝对平行的,所有的铅垂线都是指向地心,它们的虚拟延长线最终将会在地心处汇聚成一个点(如图5-3所示)。而我们实验的最终目的就是为了要证明这一点。只要能够证明地球上任铅垂线受地心引力的延展方向示意图意两点上的铅垂线之间都不平行,且方向都向同一点汇聚,就能证明地球的确是个“球”。另外使用铅垂线还有个好处就是无论你在什么地方做这个实验,也无论地面是否平整、支架是否垂直,即便出现图5-3所画的那种高山陡坡的极端情况(我画的有些夸张,只是为了让大家看清楚),铅垂线也依然能够准确无误地指向地心。
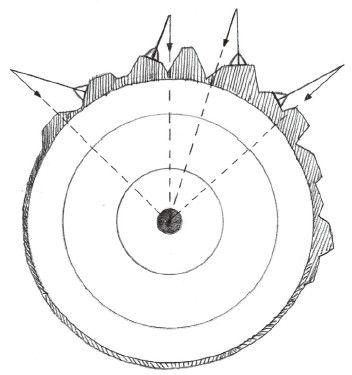
图5-3
好了,现在万事俱备,只欠行动了。让我们找一个晴朗无风的夜晚,寻一块平整的开阔地,或是广场(要注意安全哦)开始我们这次有趣的实验吧(图5-4、图5-5)。
这个实验至少需要两个人参与,其中一人将左边支架摆放到广场的一端A,打开激光笔并再次用直角尺调整激光光束与铅垂线之间垂直,要细心,要保证最高的精确度。调整好后将光束射向广场另一端B。这时另一人拿着右边支架循着光束的方向走到广场另一端,同样也要细心调整镜子使其紧贴铅垂线,保持与地平线的绝对垂直。镜面调整好后再仔细调整支架B的摆放位置、高度和方向,要使镜面正对A地点,并让激光束正好照射E到镜子上。再次调整右边支架的方向,让反射的激光束能正好返回到原位,也就是A地点。反射回来的光束能否准确回到原位并不十分重要,但至少要保证大概的位置,让A地点上的人能同时看到射出去的激光和返回来的激光就行。A点上的人拿张白纸,让反射回来的激光束照射到白纸上,并对比激光笔与白纸上光斑的高度差。实验完毕。
这个实验要证明什么?我来解释一下实验原理。
根据几何学上平行线定律,一条穿过平行线的直线与每一条平行线之间的夹角都相等。如图5-4所示,如果A点与B点上的两根铅垂线是相互平行的,那么垂直于A铅垂线的激光束也一定垂直于B铅垂线,从A点射出的激光与从B点反射回来的激光将在同一条直线上,不会有任何夹角。相反,如果从B点返回的激光和从A点射出的激光不在同一条直线上(如图5-5所示),那就能证明A点与B点上的两条铅垂线之间并不平行。根据三角形原理,如果激光的落点比出点位置高,那就证明两条铅垂线之间的交点在地表以下,在A点与B点距离不变的情况下,落点与出点之间的高度差越大就说明汇聚夹角越大,汇聚点也越近;相反高度差越小就说明汇聚角越小,汇聚点也就越远。将这个实验在东南西北各个不同方位重复多次,保证每次实验A点与B点之间的距离都相等,如果每次对比激光的落点都比出点高且高度差相同,那就能证明所有的铅垂线都将在同一个点上汇聚,事实上那个点也就是地球的地心。证明了这一点也就证明了地球确实是个“球”。
我个人认为这个表述是错误的,至少也应该表述为“几何中心”之类的吧?而且,考虑到地球表面情况的差异,也未必都能落到同一个点吧?此外,我还想在最后对这个实验的精度问题多说几句:通过这个实验,我们不但可以验证地球是球形这个事实,而且也可以根据A、B两点之间的距离和激光出点、落点的高度差计算出激光与镜子之间的夹角,进而根据勾股定律计算出激光出射点与A、B两条铅垂线汇聚点之间的距离,也就是地球半径。但我并不主张这样做,因为这个实验能证明Dr.Who提出的问题就足矣了,而要用这么简陋的工具去测量地球半径这么巨大的尺度是很困难的,原因就在于我们无法保证测量精度。在这个实验中A、B两点之间的距离越大,实验效果就会越明显,但对实验工具的精度要求也会更高,且不说激光并不是真正的平行光,在很长的距离上它依然会有一定程度的扩散,使我们无法准确判断激光落点的精确位置,就仅仅调整激光与铅垂线之间的垂直度一项任务就是一件十分考验我们耐心的工作。因为A、B两点之间的距离很远的话,比如1000米的距离,只要激光束有0.1度的角度误差,就会在B地点出现约1.125米的高度误差,而返回A地点后这个误差更是扩大到2.25米多。所以说这个实验在原理上是成立的,但具体操作时要求我们有极高的精确度,否则就会出现很大的误差,甚至导致完全错误的结果。

图5-4 激光回射实验示意图(Ⅰ)
< p>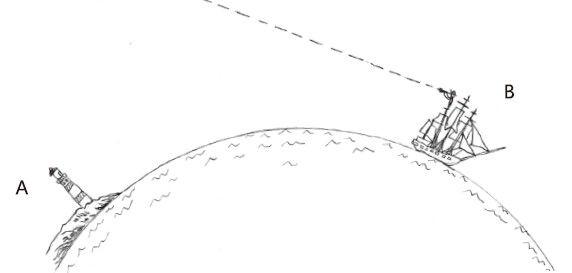
图5-5 激光回射实验示意图(Ⅱ)
松鼠“沐右”的点评:
其实铅垂线并不是严格指向地心。不考虑其他因素,地球对物体的万有引力是指向地心的,但是由于地球自转的影响,万有引力扣除维持物体和地球一起自转的向心力之后才是我们说的重力。所以实际上来说,重力并不是指向地心,而是稍微有一点偏差,不过这个一般可以忽略。另外当地的矿产分布、地形等因素也会改变物体受引力的方向,例如某个方向的地下有质量比较大的大量矿产的话,地面上实际受的引力会偏向这个方向。
这个想法如果真能操作的话,应该是可以作为一个测量地球半径的手段。但是实际操作中精度肯定很难达到。正如Aqdd在文末所说,0.1度的偏差就有很大的误差(根据我的计算,应该是1.745米而不是文章里说的1.125米)。除了激光器、镜子的摆放位置之外,风的影响,光通过的那部分空气的影响(温度不均匀会导致密度有偏差)可能都会使得这个实验得出错误的结果。
另外,这篇文章实际上还可以推导一下若A、B一定距离不同时,对应的光斑位置差别有多少,然后和可能误差对比下,就会显得更实际一些。
“Laoma”的热闹答案
关于地球是不是圆的这个问题的答案,最直接的验证方法是拍一张地球的照片。自从人类进入太空,宇航员为我们带回了很多圆形的地球照片,你对此一定不陌生。图5-6是第一张地球全景图,此照片摄于1972年,当时阿波罗17号航天飞机组脱离地球轨道,飞向月球,背对太阳,宇航员捕捉到一个完美的蓝色星球。

图5-6地球全景图(图片提供:美国宇航局/约翰逊空间中心)
如果想亲自拍摄一张足以证明“地球是个球”的照片,就要费点事了。普通照相机是很便宜的设备,但如果4000万美元的商业太空旅行也可以认为是便宜或者不受题目关于“设备价格”的E限制,那么我们可以搭乘宇宙飞船,到太空给地球拍照了。
如果大家对以上提议都不认可的话,我们就只能退而求其次,尽可能远离地球表面,在天上拍摄地平线,用弯曲的地平线,来证明地球是圆的。
实验工具:数码照相机一个,图像编辑软件一套,飞机票一张。
数据采集:在飞行过程中到飞机的窗口拍摄地平线,同时记录飞机飞行的高度。
数据处理:用图像编辑软件打开拍摄的图像,用直线工具连接照片最左端地平线和最右端地平线,在连接线的中点,数一下地平线离开直线的像素个数。
通过分析NM之间的像素与h、r的关系,我们可以进一步了解地地球半径越大,拍出来的地平线越接近直线(图5-8)。
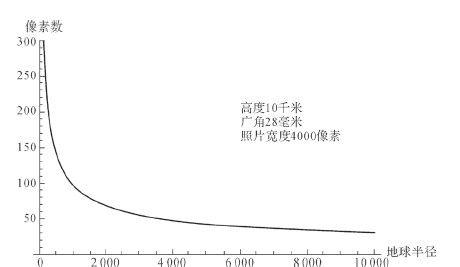
图5-8 地球半径与像素关系线图球圆球形的性质。
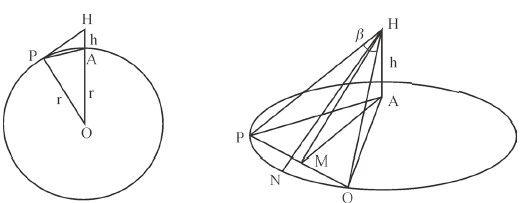
图5-7 飞机与地面投影夹角示意图
数学分析:飞机在 H点,在地面的投影是 A,所以高度是 h。
在H点,我们向地平线PNQ拍照,在照片中,P、Q分别是照片边飞得越高,拍出来缘的地平线交点,M是直接PQ的中点,N是地平线的中点,照片的地平线弯曲越厉害上N是在M的上面。对于一个照相机,在一定的最广角的放大时(图5-9)。
照相机的视角β是确定的(比如28毫米广角代表76度视野),通过地球半径r、飞行高度h、视野角度β可以计算∠NHM,进而计算出照片上NM之间的像素个数。这照片上的像素:
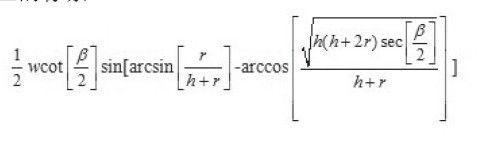
最近我没有乘飞机,拿一张以前的照片看看,由于没有记通过计算我们得到:录飞行高度,不能拿来计算地球半径。不过根据已知的地球半径可以反推出来,这张照片里面飞机离地面的高度大约是2000米3(图5-10)。
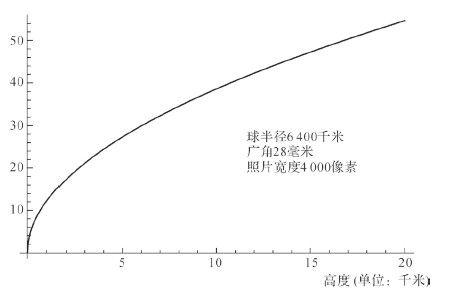
图5-9 拍摄高度与地平线弯度关系线图

图5-10 飞机上看地球表面(Laoma摄)米
松鼠“沐右”的点评
我对这个答案很欣赏。虽然这个方法不一定便宜,但是,非常有创意,而且有完整且正确的理论计算。其实好好展开一下的话完全可以媲美那个普林斯顿大学的罗伯特.范德贝(Robtert Vanderbei)根据密歇根湖的日落照片计算地球半径的方法。另外,Laoma这个方法其实在山上也可以的。这个过程实际上受地形的影响比较大,不如水面理想,而且飞机离地面的高度不好估计,为了避免当地海拔的影响,可能在飞在大海上的飞机上更合适。另外还要保证照片上地平线保持水平,或者考虑进照片上的地平线和照片横向的夹角,否则照相机视角β值的意义就不大了。
