要裹着多少气泡垫从六楼跳下去才不会摔死?我大致将高度定为20米。
解决这个问题要从哪里入手呢?首先我们需要一些气泡垫。我们可以测量气泡垫的哪些性质呢?

首先,我可以测量气泡垫的厚度。没错,气泡垫有许多种,不过我就测量我的这种(总得从某处开始着手吧)。我不是只测量一张气泡垫的厚度,而是把若干张叠在一起测出总的厚度,然后画出坐标图。
我每加一张气泡垫就量一下总的高度,然后画了一张坐标图,坐标轴分别是气泡垫的张数和高度。这个线性拟合方程的斜率为每张0.432cm,这样就能很好地估算出一张气泡垫的厚度了。
其次,我需要知道气泡垫有多“弹”。像弹簧一样吗?如果是像弹簧一样,那它有多硬呢?如果是一个真实的弹簧,那我就对其施加重量,看看它会被压缩多少。就这么干。
如果画出图像,那它看起来基本是线性的,收缩的程度和施加的力的大小成正比。所以可以说气泡垫的性质的确很像弹簧。气泡垫像弹簧一样对外物(比如人)施力,我可以为这个力建一个模型。这个力的大小和气泡垫被压缩的程度成正比。
从上面的数据可以得出这个规格的气泡垫的有效弹性常量。那其他规格的呢?假设我把两张气泡垫叠在一起,而不是单独一张,在上面施加一个重量后,每张气泡垫各自的压缩程度和单独一张气泡垫是一样的,因为它们承受的重量相同。但是两张气泡垫叠在一起的话,压缩程度的总和比单独一张气泡垫的大。
一张小的气泡垫和一张大一些的气泡垫相比的话,又有什么不同呢?这就像把两张气泡垫并列拼在一起。当在上面施加重量的时候,它们同时支撑起这个重量,所以各自承受一半的挤压力。所以两张气泡垫拼在一起时的压缩程度会比单独一张的小。
简单地说,面积越大的气泡垫,性质越接近一个更硬的(弹性常量更高的)弹簧。气泡垫叠得越厚,有效弹性常量越小。一种材料拥有的和其实际尺寸无关的硬度属性,叫做杨氏模量。已知我这种气泡垫的规格,可以得到这种气泡垫的杨氏模量为4319N/m3。
那么跳落的情况是怎么样的呢?跳落本身不会造成危险,危险的是落地。估计落地安全性的最好方法是考查重力加速度。NASA已经采集过人体所能承受的最大重力加速度的相关数据:
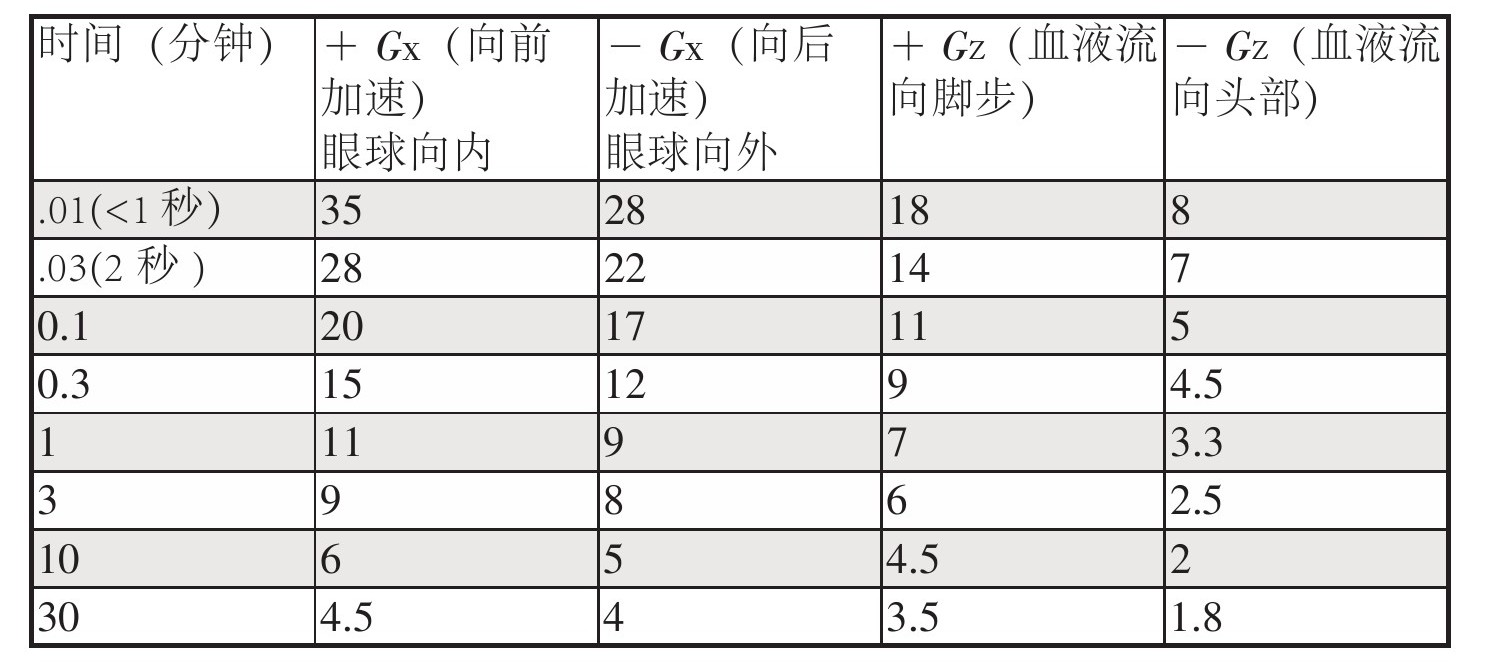
从这里可以看出,采用向前加速(眼球向内)的姿势时,普通人体能够承受最大的重力加速度。这种情况下重力加速度会把眼球向头部里面推,这意味着在跳落之后是用背部着地。
这里有个小问题。一位裹着气泡垫的跳落者在与地面撞击的时候,其重力加速度不是恒定的。下图表示的是一个裹着气泡垫的人与地面撞击的过程:

所以,这时候人体主要受到两个力的作用:来自气泡垫的力(像弹簧一样)和地球引力。要想使跳落者停下来,重力加速度的方向必须朝上,而气泡垫所施加的力必须大于地球引力。
重力加速度的大小取决于弹性常量以及弹簧被挤压的长度。这两个值我都不知道。不过,我可以利用功能原理来考查整个降落过程。在降落的起点终点,动能都为零。在降落的过程中重力势能会减小,而在撞击的过程中气泡垫的弹性势能会增加。由于没有外力对这个系统做功,我可以建立一个跳落高度和所需的弹性常量(以使重力加速度在可接受范围内)的关系。
要求出k的值,我还需要知道其他一些值。下面是我做的假设:
跳落者加上气泡垫的总质量为70kg。这里我假设气泡垫的质量比跳落者小。
最大重力加速度为300m/s2,撞击过程的持续时间不超过1s。
跳落的高度是20m。
这样的话,要使落地时的重力加速度不超过NASA所给出的人体超重耐力,气泡垫的弹性常量应该为1.7×104N/m。
现在我知道要使跳落者停下来所需的弹性常量,我离知道需要裹多少层气泡垫又近了一步。首先,我需要估算一下地面和气泡垫的接触面积。我知道在撞击过程中,这个面积其实是会变化的,所以我只能估算一下。假设撞击时地面和气泡垫接触的面是一个0.75m见方的正方形,接触面积就是0.56m2。
已知气泡垫的杨氏模量,可以算出所需的厚度(我任性地用L来表示)为0.142m。因为每张气泡垫的厚度为0.432cm,所以我一共需要39张。
39张气泡垫也许看起来有点少,我来计算一下气泡垫的质量还有它看起来有多大。我假设气泡垫在跳落者周围裹成一个圆柱体,那它看起来差不多是这样的:
从上往下看,这个人看起来大体上是一个半径为0.3m的圆柱体(只是猜测)。如果气泡垫额外地延伸出0.142m,那么气泡垫的体积是多少?哦对了,我还要设这个人的身高为1.6m(也是猜测)。这样气泡垫的体积就是0.53m3。
我可以利用气泡垫的厚度和质量的数据算出气泡垫的密度。这么大体积的气泡垫的质量就是9kg——还不赖。不过,严格来说这会改变落地所需的气泡垫的数量。或许为了保险起见,我可以再加几层气泡垫,以抵消气泡垫本身的重量。
既然知道了人裹上气泡垫后的体积,我可以考虑一下降落时的空气阻力。在空气阻力的经典模型中,阻力大小与物体的横截面积以及物体降落速度的平方都成正比。
因为当速度变化时,阻力大小也会随之变化,所以这个问题在纸面上不太容易解决。不过,要是用计算机把这个问题划分成许多短的时间间隔,那么这个问题计算起来就很直观了。
在做这个数值计算的时候,我得到下面两个关于降落物体位置高度和垂直速度的坐标图。
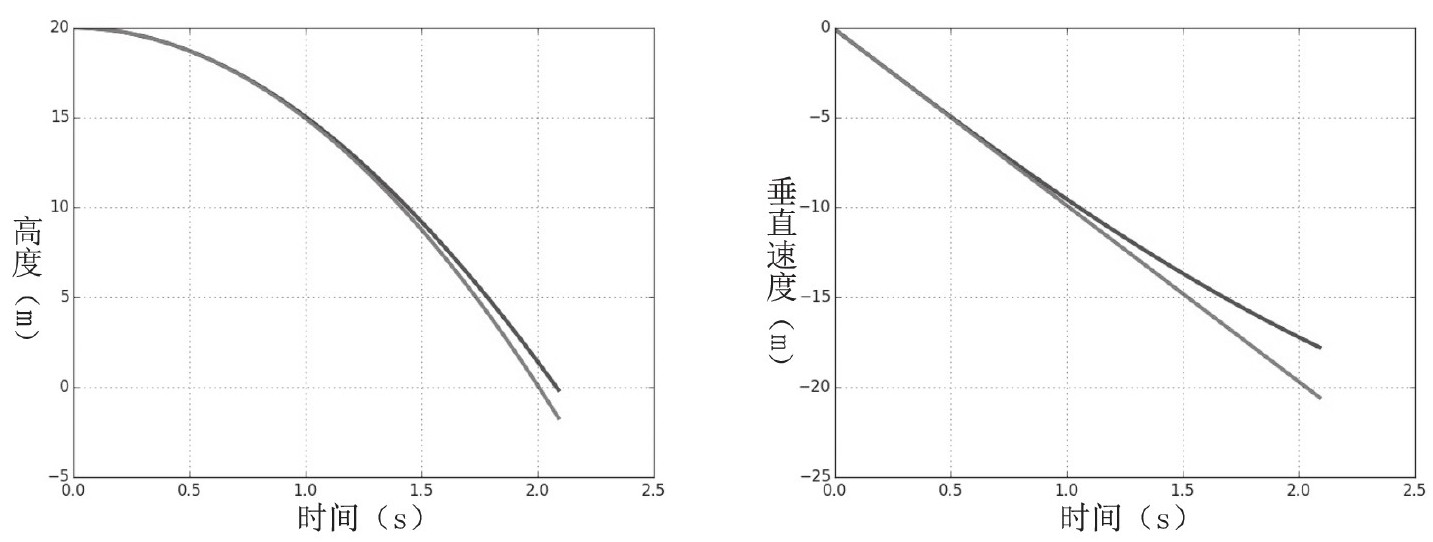
上图表明,考虑到空气阻力的话,降落物体在撞击地面之前的速度会稍微低一些(为17.8m/s,而不是大约20m/s)。我可以把全部数据重新算一遍,但是我不会算了。不过你可以把这个较低的速度考虑为安全极限范围(尽管我绝不会认为这种事情是“安全”的)。
再留一道附加题给你当家庭作业怎么样?要从一架飞机上跳下去而不摔死,你得裹多少气泡垫?我猜不会比从楼上跳下去多太多。如果你再加几层气泡垫,就会降低物体降落的终极速度。
不过我们真的要用气泡垫来保证人的安全吗?这显然不是一个好主意。
