我偶尔会瞥一眼电视上的政论节目。有一次,我看的一档节目讨论的是国债和对不同项目的资助问题。一位参与者提出这样一个说法:如果把1兆美元的纸币(我猜是面值一美元的)叠起来,可以在地球和月球之间打4个来回。
我并非不相信电视上的人所说的话,只是我想验证一下,而且这个数值看起来也是能估算出来的。
一张1美元的纸币有多厚?我的钱包里不经常装现金,不过当我装的时候,我就测量一下。一共有5张纸币。我测量了一张纸币的厚度,然后测量了2张的厚度,以此类推。以纸币的张数为自变量,以纸币叠在一起的厚度为因变量,可以画出一条直线,这条直线的斜率为0.1mm/张。这就对一张1美元纸币的厚度做了一个不错的估算。
那么1兆的1美元纸币叠在一起有多厚呢?首先,1兆是多少?很不幸,大家观点并不统一。在美国,1兆等于1000个10亿,也就是1012。而在某些国家,1兆等于10亿个10亿,也就是1018。很容易混淆,我知道。我在这里计算的时候,取1兆等于1012,因为这档节目是在美国播出的嘛。
那么1012张一美元纸币叠在一起有多高?首先我们假设纸币的厚度不会被压缩。为什么要这样假设呢?我不知道,可是总要从某个地方入手吧。这叠纸币的高度就等于1张纸币的厚度乘以1012,也就是108m。

地球到月球的距离大约是4×108m。好的,那么问题就来了。根据我的计算,1012张1美元纸币叠在一起的高度是地月距离的1/4。而节目里说这些纸币叠在一起能在地球和月球之间走4个来回,也就是3.2×109m。
现在我来算算另一个问题。如果1012张1美元纸币叠在一起,真的能在地球和月球之间走4个来回,那1张纸币得有多厚?我只要把地月距离乘以4倍,再除以1012张,得到每张纸币的厚度为3.2mm。
1张纸币有3mm厚,那也太不方便了吧。所以我认为他们关于1012张纸币的说法是不对的。再聪明的人也会犯错。
好,既然他们错了,那么针对1012张叠在一起的纸币,我们还能做些什么呢?我在想究竟能不能把某件物品叠得那么高。
假设可以把纸币完美地叠起来,随着纸币越叠越高,这叠纸币被轻轻一碰就倒掉的可能性也越来越高。请看一张示意图:
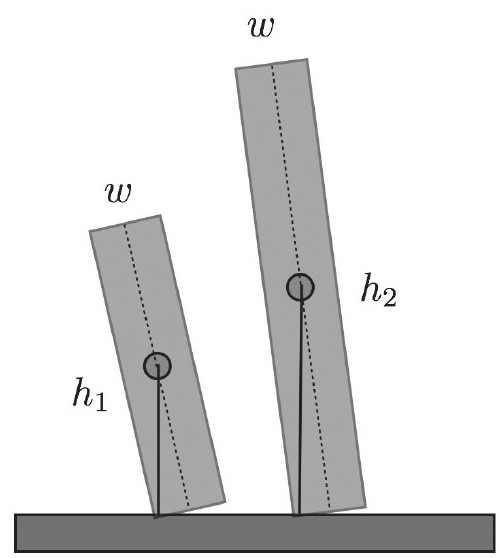
每叠钱上的那个点代表这叠钱的质量中心。如果这叠钱倾斜到使其质量中心偏出底面边缘,那这叠钱就会倒塌。是的,我假设所有的纸币都粘在一起。不过你会发现,纸币叠得越高,倒塌所需的倾斜角度就越小。
通过计算不同高度的纸币的“翻倒角度”,我发现一叠10m高的纸币只需要倾斜0.37°就会达到倒塌的临界点。如果叠得再高一些呢(你知道也不能再高多少了)?如果把纸币一直叠到104m的高度,会得到下面这张坐标图:

要是把纸币叠到106m那么高,翻倒所需的倾斜角度为3.8×10-60°。而一万亿张纸币叠起来的话(假设整叠纸币处在恒定的引力场中,现实中这是不可能的),其倒塌所需的角度仅为3.8×10-80°。这么小的角度相当于在水平方向上移动区区6.6cm。
就算这叠纸币不倒下,有没有可能叠这么高呢?处在底部的纸币能承受住上面所有纸币的重量吗?这就和所谓的“抗压强度”有关。大体上,纸张要保持完好,只能承受那么多的压力。
纸张我不了解,不过木头的抗压强度是3到37MPa。我们随机取20MPa作为一张美元纸币的抗压强度。
这叠钱的底部要承受多大的压强?这等于上面所有东西的重量除以纸币的面积(约为6.6cm×15.6cm)。这说明压强会随着高度线性地增加(假设引力场恒定,尽管这不太真实)。
利用这个压强和纸币密度的估值958kg/m3,1012张1美元纸币叠起来后,底部的压强会达到9.7×105MPa。不过其实应该小于这个值,因为海拔越高,地球引力越小。我认为这一点可以忽略不计。底部的压强远远大于20MPa这个我估计的纸币抗压强度。
好吧,既然把这些纸币叠起来不可行,我就用1012张纸币造一个小行星。已知1张1美元纸币的密度,可算出1012张纸币的质量。干嘛要用现金造出一个庞大的球体?干嘛不呢?你可以把它叫做“钱星”。首先我来算一下质量。如果每张纸币的质量为6.91×10-3kg,那么1012张纸币的质量为6.91×109kg。假设密度恒定,那么这个球的体积为7.2×106m3。
如果这个“钱星”是个正球体,那它的半径就是120m。看上去这好像不是一大笔钱,不过这个球体的直径可是长达240m。你可能对这个没有什么概念。我再打个比方,这大概是4艘尼米兹级航空母舰的体积之和。
或许节目里的人应该转述一下桃乐丝·帕克的话:如果政府把它拥有的所有的钱全叠起来,那景象我看了也不会太吃惊。
