欧洲航天局有一种宇宙飞船是自动转移飞行器(简称ATV)。ATV的主要功用是为国际航空站提供包括食物、水、氧气、科学设备和散装糖在内的补给。是的,我把食物两次列在名单之上。虽然糖果也属于食品中的一种,但我把它单独列开,为的是方便我在太空条件下考察它。
想想看,假设有航天员要求ATV额外送一包散装糖。要把糖送入轨道意味着要消耗更多能量,但需要多少能量才够呢?

首先,让我来得出一些原始数据。其中有一些数据是我大胆假设下的成果,但也许也是合乎情理的。假想国际空间站的轨道位于地球表面420km处,运行速度是7700m/s。要计算运送补给消耗的能量值,纬度和速度是两个非常重要的因素。
还有另外一个信息也是我们所需要的:ATV发射台的位置。这个位置是在法属圭亚那的库鲁,纬度仅高于赤道5°,这个地理位置的选取背后有道理的,我们稍后再回到这个点上来。
哦,最后还有一个方面。一包散装糖的质量是多少?我可不想单独指名道姓地选定某个品牌的糖果,所以我索性就取一包普通巧克力糖的质量——50g,250cal(先说明一下,这里指的是食物卡路里,即大卡,和化学卡路里不一样)。
食物卡路里和科学卡路里有什么区别?两者都是用来衡量能量的,但是1食物卡路里等于1000真实卡路里。能量有两种表述方式:卡路里和焦耳,我不知道为什么一个物理量存在两种单位,但是我个人倾向于认为这和食物和吃食物的人有密切的关系。对于卡路里的标准定义为(有时被称为化学卡路里)1cal就是让1g水温度升高1℃的能量大小。这个定义对于化学而言是合适的,但是在物理里面,我们一般选择J作为能量单位。两个单位之间的转化是1cal=4.187J。
现在,我们再来学学相关的物理学知识。为什么运送东西到国际空间站会需要能量?好吧,为了让空间站的宇航员能吃上糖,你需要完成两项任务。首先,你需要将糖果运送到国际空间站的高度;其次,你需要增加糖果的速度,让它和国际空间站的速度同步你才能顺利地把食物对接上空间站。让我来分别分析一下这两项任务到底要怎么去完成。
假设你在地面上看到这50g重的糖,捡起来到1m的高度,再放上圆桌。整个过程需要你对糖果做功,改变它的能量状态。但到底需要多少能量?其中有一个办法就是通过计算重力势能差来计算。在地球表面,重力势能的变化可以通过下列公式来计算:
ΔUg=mgΔy
其中g是当地的引力常数,一般取9.8N/kg。把一包糖果提升1m需要0.49J的能量。这个量并不多的。
假如我要把糖果的高度增加到国际空间站的高度呢?我能否用相同的计算方法直接把距离从1m改为420km就算大功告成了?不行。以上计算重力势能的前提是物体的重力是恒定的。这个前提对于近地表的物体是成立的,但是随着高度增加适用性越来越低(尽管国际空间站的高度还不致于让你的计算结果那么不精确)。
如果我们考虑到上述因素换用一个更好的模型,这个重力势能模型应该如下:
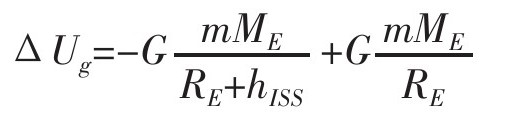
公式里,G是万有引力常数,两个质量分别为糖果的质量与地球的质量。分母是距离地心的距离。糖果的最终位置是国际空间站海拔高度(我称之为hISS),起始位置是距离地心距离为地球半径RE的位置。
如果把G的数值、地球的半径和质量代入公式,计算结果为1.93×105J,即需要这么多能量才能把糖果送上指定的位置。
尽管如此,这还不算是运送糖果所需要的全部能量。因为假如你花那么多能量只是把糖果运送到某个位置就不再理会了,最终它还是会从太空坠回地球。要完成整个任务,糖果还需要动能,即运动的能量。物体的动能是质量与速度的两次方相乘得数的1/2。
国际空间站的速度是已知的,所以计算起来很简便吧?如果我把糖果的质量0.05kg和7700m/s的速度代入,其结果就是1.48×106J。事实上,这个答案还是不对的。为什么?考虑不够全面。因为我们的计算方式默认是将糖果从零速度状态下开始加速,而在开始加速前,糖果已经处于运动状态了,因为它是在自转的地球表面上的。
地球的自转周期是24小时(更精确地说也不是这个时间,24小时只是太阳回到原来位置的时间,但这个时间对于我们的运算在精度上已经足够了)。所以我们的计算方法就是拿发射地纬度的圆周长去除以24小时,从而得到糖果的速度。
为什么纬度也很重要?想象一下糖果在地球表面随着地球自转做圆周运动,运动的圆周半径是多少?在赤道,圆周半径和地球半径是一致的。然而,在北极圈的中心位置,糖果根本就不会做圆周运动了,只是在原地自转而已。圣诞老人酷爱甜食,希望圣诞老人不会选择去北极上空的位置吃糖果,那样给他老人家送上去就未免太强人所难了。
如果和地球赤道离得很近,运动的圆周半径基本上和地球半径相等,初始速度就达到464m/s。这个速度和国际空间站的速度相比很小,但不能否定它还是有点微弱作用的。这就是欧洲航空局选择从库鲁而不是在欧洲其他的地方发射ATV的原因。
行了,糖果自身有动能,抵消之后还需要多少动能?从赤道发射你需要1.47×106J的动能。
把糖果运送到国际空间站所需的能量总和,来自于两个我们已经计算出的结果:动能的变化量与重力势能的变化量,两者之和是1.66×106J。要把一小包糖果送上天居然要消耗掉百万焦以上的能量值,并且我们的计算效率还是理想化的——即在运送过程中没有任何能量的损失,百分之百的能量都被用于把糖果送至轨道。大概我们不住在太空的原因就是这个,要送点东西实在是代价高昂。
要对百万级的能量有个感性认识很不容易。我不妨就拿糖来类比一下。这包糖被吃掉之后会产生250食物卡路里。1食物卡路里等于1000cal,4180J。
让我们回到问题上来。假如我们要耗费1.66×106J的能量把糖送上轨道,这么多能量是多少食物卡路里呢?显然,这个就只要把单位转换一下就可以算出来了。记住单位转化的秘诀在于做乘法运算的时候要保持一标准单位的量。举个例子,1英尺≈0.3048米,所以1.2英尺要化成米就是把1.2×0.3048。这个分数的分母为一个标准单位,实际长度大小不变,只是单位转化了。
根据单位转化的结果,我计算出能量是1.6包糖。好吧,这个结果还在可接受的范围之内。原来真要把糖送上国际空间站,消耗的能量只不过1包多的糖的能量那么多而已,没有想到居然那么少。
最后还有一个问题:如果我只用糖作为能量把所有ATV上的货物统统都送上站行吗?ATV满载货物时质量为20吨,即20000kg。如果货物全部是由糖构成的,那总量就会有400000包糖了,可如果你要想着把那么多糖一次性送上站,那总需要640000包糖的能量那么多。
