在十项全能比赛里,运动员要参加10个赛事的争夺(所以有“十项”之说)。然而,会存在一个问题——多人同场竞技,每个人要参加10个之多的项目,他们之间如何一较高下?还有更成问题的问题:10项比赛中有4项是以秒计算的,其他6项则用米来计成绩。再有,即便是以距离为比拼的项目中也还有问题,因为要把跳远的距离拿来和标枪投掷的距离相比也是一件棘手的事情。
所以要怎么样才把这些成绩拿来相比?有一个办法就是提出一种公式,可以代入各种比赛的成绩,经过公式处理之后给出一个数值。为了公平起见,十个项目需要保证相互之间的权重相同。这个目标说起来容易,实行起来很难。然而,确实存在一个可以为每项比赛计算得分的一个公式,这个公式是这样的:
时间项目的比赛分值ST=A(B-P)C
距离项目的比赛分值SD=A(P-B)C
其中,P是比赛获得的成绩,A、B、C是分别是根据比赛不同而改变的常数。你可以观察到这里有两个不同的公式。对于时间项目比赛而言,时间越短分值越高,因为有某个常数减去这个时间,对于以距离长度取胜的比赛,情况恰好相反。
单位呢?没错,你第一眼看过去这的确像是一个麻烦,但事实却是你担心过度了。首先,让B和P的单位统一为秒或者米没有多大的意义,即便你这样做可以给B和P做减法(单位不统一无法进行减法)。如果你真的让B也有了单位,最终又要是一个无单位的数值,那常数A的单位就需要变得像米-1.81那么离谱(因为C可能是1.81)才能消掉单位。因此,我的建议是换一种方式,A设置成一个p/k形式,并令其中k变成1m。这样一来,你马上可以消掉这个单位了。
有一个关于十项全能得分的视频,非常有趣,它向我们展示了一个现象:对于任何一项很差的成绩,最终得出的分是你想都想不到的,比方说为一个负数开立方根。事实上,你得到的是一个很复杂的结果(其中一半是真,一半是虚的)。
很可惜,我很确定地说官方条例已经考虑到了这点,并且规定好了凭这种出奇的方式是无法取胜的。如果真的有谁能真的靠这个方式来赢得比赛,那倒真是一件奇事了。
到底哪个项目最为紧要?就像我刚才说的,我们的目标是让所有的比赛项目权重相当。但是,如果你以0.01s的微弱优势打破了世界纪录呢?这种情况下,你的分数怎么体现?还有,如果你以同样的0.01s时间打破的不是100米的纪录而是400米的纪录,得分又会有什么变化?对于你的总分而言是好是坏?

首先,还是让我们集中于一个项目来考察——跳高。不同的距离怎么得出不同的分数?世界跳高纪录是245cm。以下这幅图表示的是达到世界水平50%~105%区间内的分数情况。
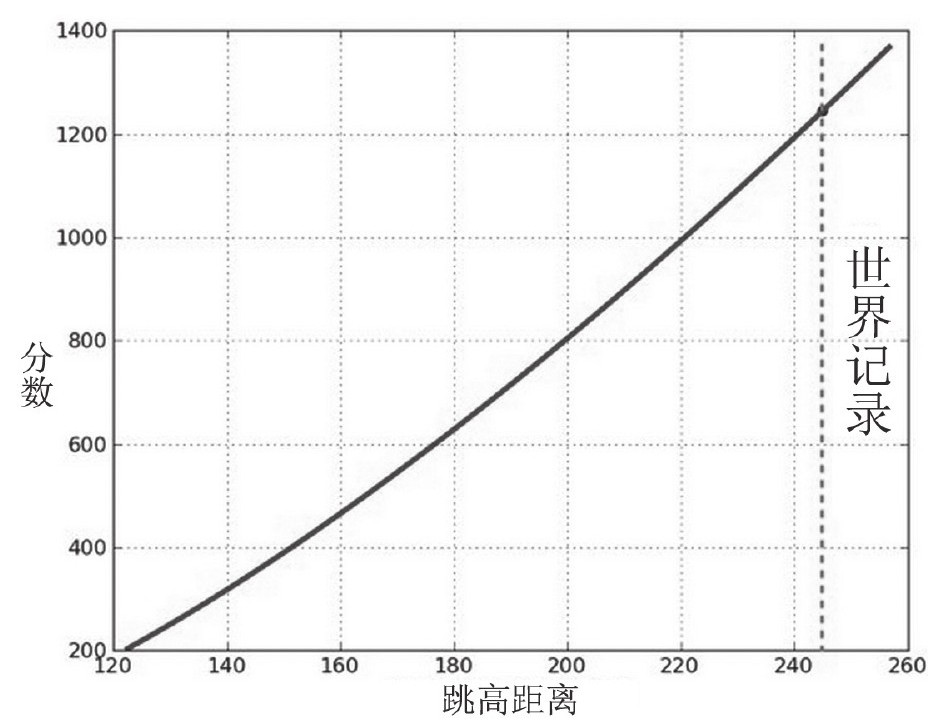
对于这项世界纪录,达到的运动员能取得1244分。这个分数很可观,因为整个十项全能的分数也只有9000分而已。跳高这个项目很能说明问题,因为它的相关系数C不如推铅球项目的相关系数那样接近一个数值。
所有运动项目得分分布如何比较?有一个办法是拿比赛的成绩比上世界纪录,得到一个比值。这样,100米的世界纪录9.58s最终就是一个无单位的表现值:1.0。假如你以9.57s打破世界记录,你的表现值是1.001。如果你对其他项目也以同样的方式处理,所有的比赛成绩就可以相互比较了。
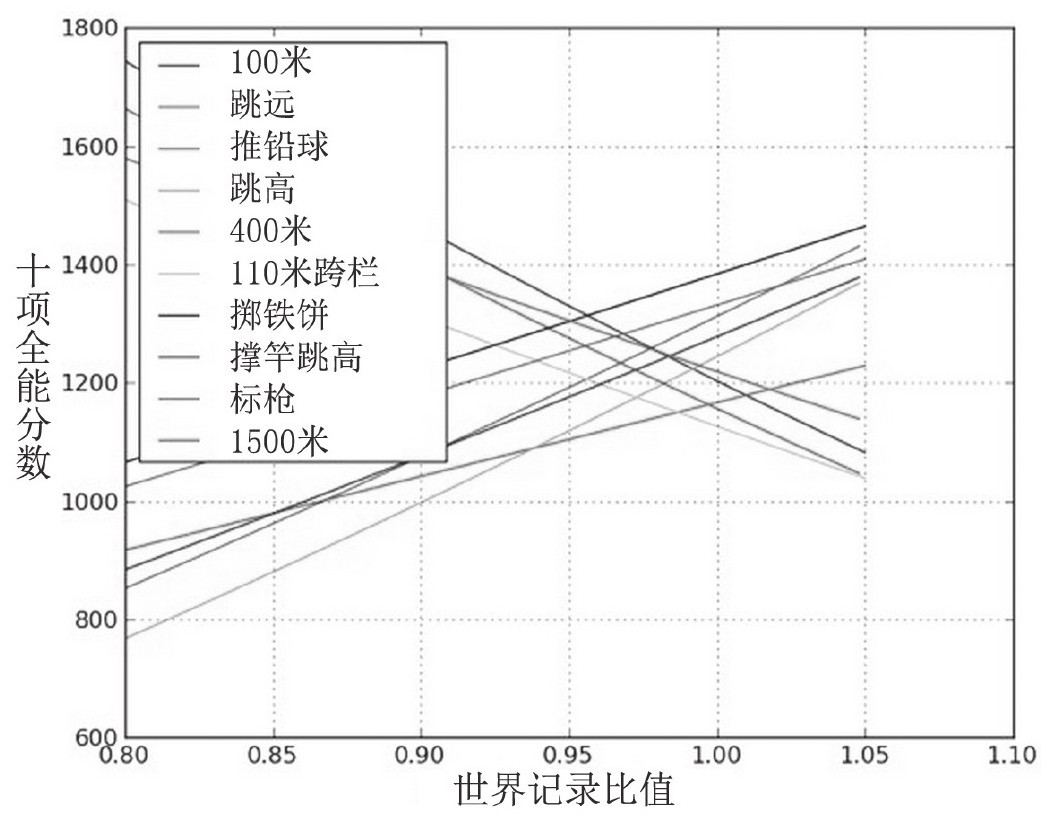
下面这张图展现的就是十项全能比赛的每一项成绩与得分之间的关系。请注意对于以时间项目比赛来说,花的时间越少,分数值越高,这也就是表示这种运动的线的斜率是负值的原因。
你从这幅图里能看出什么来吗?如果你能打破一项世界记录,你最佳的方式是把这项记录放在掷铁饼这个项目上,因为这个世界记录一旦获取将会给予你1382分,比较一下110米跨栏,你会发现打破世界纪录给你的比分只有1123分。
那成绩进步呢?你可以在距离和时间方面都取得了进步,选哪一种运动更划算?本质上,这是一个分析表现变化会导致分数相应变化程度的一个过程,这就意味着我要算每一个值的导数。将导数代入两个公式(关于P),会得到:
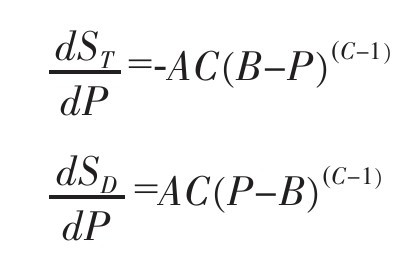
当然,你可以代入A、B、C的值来决定分数的变化率。这个变化率不是一个常量,而是一个取决于运动员表现的值。所以每次计算你得代入不同的值,比如你的时间成绩和世界记录的时间成绩。然而,有一个更为简便的近似方法。以上项目的图里,在世界记录附近斜率最高的是哪项运动?对于时间项目运动而言,是100米短跑,对于距离项目来说是跳远。但请你记住,这张图体现的是基于世界记录的比赛成绩变化引起的得分变化。在100米短跑中取得5%的进步和1500米长跑中取得5%进步难易程度相同吗?也许不同吧。这也是为什么对于任何一个项目要想夺得高分没那么容易的原因。
