我们还有另外一种方式,可以考察鲍勃·比蒙在1968年夏季奥运会创造的跳远纪录。假设我以每次纪录被打破的日期与当日成绩对应作图,会得到如下这张男性运动员与女性运动员的散点图。
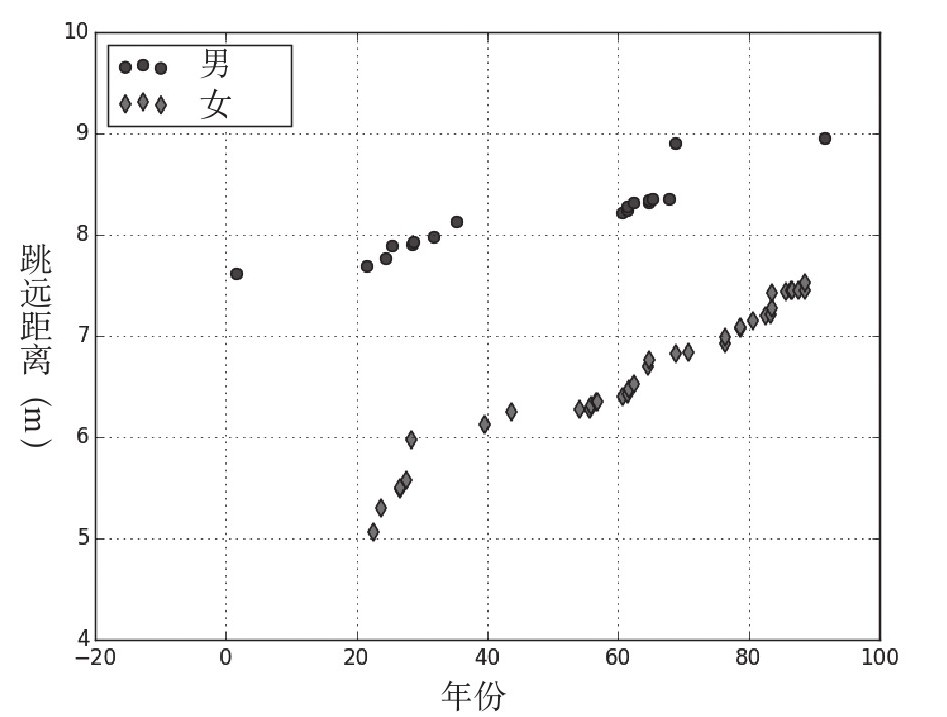
让我一直很惊讶的是世界纪录的推进几乎是以一种线性回归的方式进行的。让我从女性运动员的数据开始解读。为了让解读更具有说服力,我先找到能反应这些数据的函数,这一过程即是线性回归。

如果我能够找到代入这些数据的线性公式,我得到的函数如下:
sw(t)=(0.0314m/year)t+4.656m
这个线性模型和数据的吻合程度很高。如果你代入年份数据,这个模型很快就会为你预测该年份跳远的世界纪录(1967年为67,2012年为112)。公式里的4.656m呢?这个是由模型计算而得出的数据,反应的是1900年当时的运动员水平。显然,在那个年代还没有任何记录,因此我认为那时候人们的实际运动水平应该远不止于此。
这里还有一个很有趣的现象:我用这个模型推导出0.0m这个成绩产生的年代,结果公式给出的是1885年。没错,这个结果让人贻笑大方,这也就从侧面说明这只不过是一个简单的、并非万能的模型而已。
还有一个现象也值得注意:我同时也计算了一下反应这个线性模型与这些数据吻合程度的相关性系数。这些数据的相关性系数为0.98。我们知道相关性系数为1.0的时候,数据与模型的吻合程度是最佳的。0.98说明了数据和线性模型之间的相关性非常高。
现在转而解读一下男性运动员的纪录。假设我找到一个可以覆盖掉除最后两个数据以外所有数据的函数,我注意到鲍勃·比蒙在1968年创造的纪录在图中仅次于最后一个纪录——1991年由迈克·鲍威尔创造的跳远纪录。如果我把这两个数据予以忽略,我就可以暂时忽略掉鲍勃·比蒙那次超常规的比赛成绩。
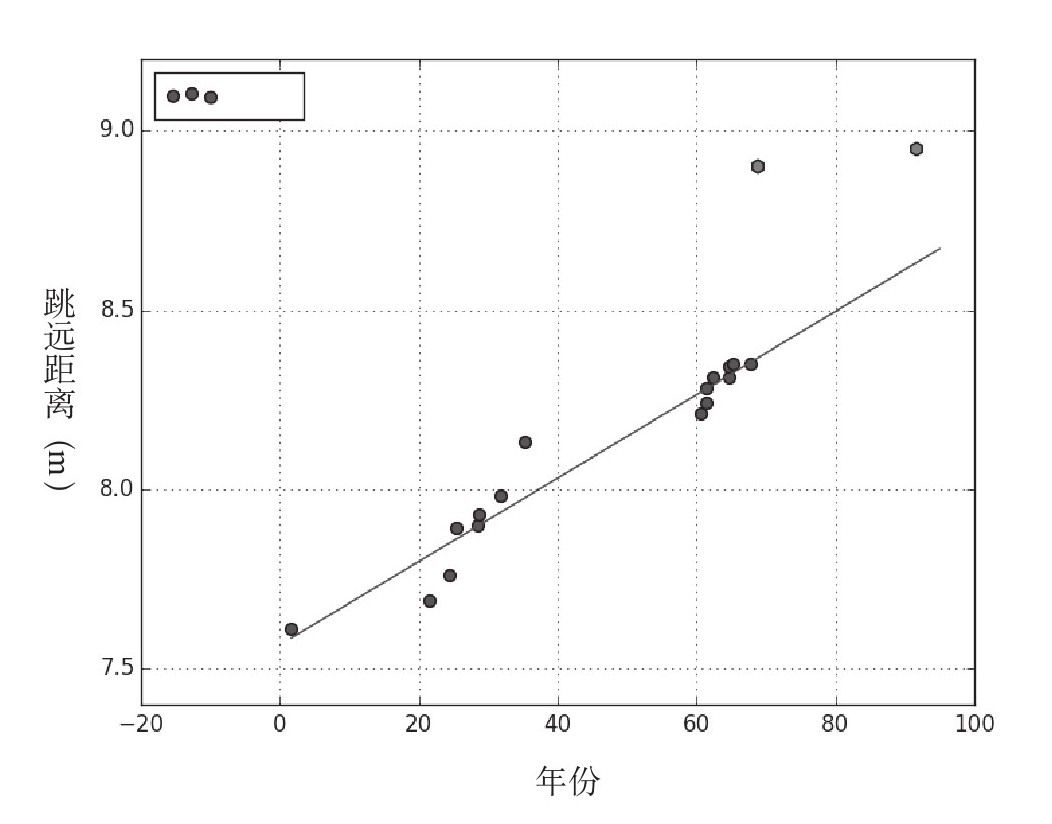
假如忽略掉最后两个数据,你可以发现这条线性函数与前面的数据吻合程度很高。有了这个函数,我可以算出它的斜率为每年0.0116m,截距为7.57m。
显然,如果把两人的纪录“舍弃”在函数之外,所有的数据都可以被这个函数纳入进来,并且可以做出这样预测:跳远成绩要达到8.95m将要到2018年才能被人类取得。
虽然这些模型中在大多数情况下都能够起到作用,但如果有时一种运动上的新技术一旦出现就可以完全改变模型。举个例子——著名的背越式跳高,跳高运动员的跳法是以垂直的方式跳过一根水平的杆子。在1965年以前,人类一直是使用普通的方法跳高,且效果不错。然而在1965年,迪克·福斯贝里率先使用了背越式跳高技术,在动作上不再以面朝杆脚先着地的方式过杆,而是扭转身体让背部朝杆头先着地的方式过杆。他的这种新技术使他迅速打破了原先的世界纪录,同时也使得以前已经确立好的世界纪录产生趋势瞬间得以改变。
我不清楚比蒙和鲍威尔打破纪录是否使用了不同的跳高技术,但是他们各自都属于不同的阵营。让我们等到2018年来看看原来的模型是否还是具有预测的效果,因为根据模型,2018年该是有人出来打破鲍威尔纪录的年份。
最后,我们来观察一下男性纪录的斜率(0.0116米/年),女性的斜率(0.0314米/年)。两者之间差距巨大。女性运动员成绩新纪录产生的速度要远远快于男性运动员。如果两个模型仍然可以起到一定的预测效果,那还要多长时间女性的跳远能力才能和男性平起平坐呢?
我所要做的就是让男性与女性跳远的距离相等,然后求解出具体年份就可以了。这个问题很简单,是二元一次的方程组问题,所以我就不劳你费力计算了,我直接告诉你答案就可以了。
如果我把147年这个时间数值代入两个公式,两个公式最终显示的成绩都是9.27m。由于我设定当t=0代表1900年,所以这个纪录应产生于2047年。
当然,我自己也很怀疑到底这些模型能不能预测那么多年以后的未来。根据电影《终结者》我们已经知道2029年整个地球都会受机器人统治,也许到了那个时候我们会决定让机器人来代替我们参加奥林匹克,那数据就得完全改写了。
