力对于物体产生什么作用?对于物体而言,力到底起到什么样的作用?我们知道,力是物体间的相互作用。在最基本的层面,我们可以把世界上各种各样的力划分为4种:引力,是有质量的物体间的相互作用力;电磁力,是带有电荷的物体间的相互作用力;强核力,是像质子和中子这样的粒子之间的短程相互作用力;弱核力,是亚原子粒子之间的相互作用力。最后两个力和这节我们要讲的愤怒的小鸟TM这个游戏并不相关,所以暂时不讨论。
如果一颗球被某人一扔,不小心砸到我的头,我头上挨了一下。挨了一下,这是个什么力?从物理技术上来讲,这属于电磁力。球的原子和我头部的原子里都含有电子和质子,当它们相互接近时,有这些带电粒子之间形成相互作用的电磁力。表面上,我是被球击中了,但真的是“我”被击中了吗?在原子水平上,很难界定“碰撞”这一概念,我们只能说,球的原子和我头部的原子发生了相互作用。
好吧,我越来越偏离正题了。回到引力,引力是一种什么样的力?引力是任何有质量的物体都与其他任何有质量的物体之间发生的一种相互作用力。然而,这种相互作用力很弱。通常情况下,除非两个物体中的一个物体具有非常大的质量,不然,我们甚至不会注意到这种相互作用的引力。
为了加以说明,给大家举一个例子。假设我拿起铅笔再放开手。铅笔和地球都有质量,我也有质量,但铅笔的质量和我的质量并不大,这就决定了铅笔和我之间虽然有引力作用,但非常小,也不会产生什么显著作用,因而无需加以测量。但是地球就不一样了,它的质量是非常巨大的,它造成的引力足以影响到我放手之后铅笔的运动,于是铅笔就产生自由落体的物理现象了。
回到一开始提到的第二个问题上——力到底对物体产生了什么作用?简而言之,力改变物体的运动。在这句简单的话中,“运动”这个概念举足轻重,我们千万不要落入别的大多数人都会落入的圈套里。大多数人会说的是:力是导致物体运动的原因。在某种意义上,他们可能也有一定的道理,但是在大多数情况下他们的认识是错误的。在这里,我准备了一个很好的问题正好可以测试一下你的家人和朋友是不是也持有这种错误的想法,这个“试金石”式的问题是:如果在物体上施加一个单一的大小不变的力,物体会发生什么物理现象?我敢打赌,96.7%的应答者会这样回答你:“大小不变的力当然让物体以不变的速度运动啊”。
但不幸的是,这种恒力导致恒速运动的想法是完全错误的。这个错误的源头在亚里士多德。之所以包括亚里士多德在内的人都这样认为是因为这个观点虽然谬误,但却很符合我们日常生活经验,而在现实中我们又很难理想地做到只让一个力单独地作用在物体上。假设你真的在现实中能够做到只让一个力单独地作用在物体上,你会发现一个恒力事实上是在不断地改变着物的运动状态的。并且,如果只在一个方向上对原本静止的物体维持着这样一个恒力,该物体的速度还会不断增加。
那么在一个恒力的作用下,物体运动的变化程度是怎么样的?让我继续来讲述这个问题。我先把这种“运动的变化”称为“加速”。一个物体的加速度取决于两个因素:力的强度和物体的质量。力越大,加速度更大;物体的质量越大,加速度就越小。可能你知道这等同于牛顿第二定律的表述,用数学公式即“合外力=质量×加速度”。
关于力,还有一方面需要我们加以清晰地认识。还记得之前提到的铅笔自由落体吗?铅笔具有质量,地球也有质量,铅笔会不会对地球也施加了一个力?是的,它也会对地球施加一个力,并且这个力在大小上等于地球对铅笔施加的力。两个力虽然相同,但结果区别很大,原因就在于质量。就像我之前说的,地球的质量是巨大的,这表明如果地球要获得一个显著的加速度,力还需要足够大才能起到效果。所以,尽管作用在铅笔上和地球上的力具有相同大小,但一个力产生了很大的加速效果,另一个却丝毫没有。
以上所讲的就是物理里的运动学在我们这个世界里的运作方式。让我们用这些物理知识为基础来研究一下愤怒的小鸟TM,分析一下在这款游戏创建的世界里的物理学是不是和我们的现实世界具有相同的运作方式?我还是等等,可能你还是不知道愤怒的小鸟TM是什么?请告诉我这不是真的。唉,还是先让我为这款非常流行的游戏铺垫一下,为还没玩过的人做一番简要说明。

从原理上讲,游戏的玩法很简单。玩家将弹弓上的小鸟弹出去,砸到被猪棚保护的绿色肥猪,将肥猪全部砸倒就能通关。猪棚可以由玻璃,木材或石材制成。为什么向猪射击?为什么小鸟会生气?为什么它们不能直接一飞了之?很遗憾,我并不知道这些问题的答案。但我知道这个游戏非常神奇,能让人上瘾。你可以在几乎所有的智能手机和PC上玩这个游戏(甚至在谷歌的Chrome网络浏览器上)。
我想我应该再稍微具体地讲一下游戏的玩法。愤怒的小鸟TM里有不同种类的鸟可供你射击。不用挑到底使用哪种鸟,你要射击前,游戏已经为你事先设定好了。不过,不同的鸟完成的任务却大相径庭。
如果你刚开始玩愤怒的小鸟TM,第一关为你提供的是红色鸟(以下我会简单地叫它小红)。如果把小红弹出去会发生什吗?小红在空气中以抛物线的路径运行。原来这正是我们称之为抛体运动的一种物理运动形式。那么究竟小红为什么它会以这样一种方式运动呢?
当小红离开弹弓以后,只有一个有意义的力作用在小红之上,那个来自于弹弓的力只是瞬间完成其作用。尽管你的直觉可能促使你思考是不是应该把这个力也添到物体上,但请不要添加,因为事实是小红在离开弹弓以后,这个力并没有始终伴随着小红在空中移动。假设你把这个力添上了,你就是在和亚里士多德交谈了,这个问题上你千万对他要闭耳塞听啊。为什么会只有一种力?试着这样去思考:你可以在这时把力统一划分为两大类:有一种力是由物体“接触”了一下另外一个物体而产生的效果,是瞬时性的,而另外一种力则恰恰相反,它是因长时间而非一时“接触”另一物体而产生的作用效果。当小红离开了弹弓之后,你分析一下会有什么力在“接触”小红呢?你认为是“空气”?但来源于空气的那个阻力实在太小了,在这种情况下几乎可以忽略不计。那还有什么力呢?没有任何力“接触”小红了。会不会有别的长时间发生“接触”的力呢?有,那正是地心引力。小红在空中的独特飞行方式正是弹弓瞬时施力之后与地心引力共同的作用下造成的结果。
因为小红的飞行只受到引力作用的影响,那我应该进一步探讨的是重力。在地球表面,我们完全可以为引力建模。引力大小恒定,方向竖直向下,这个力的大小是物体的质量和引力场的乘积,其中引力场大小为9.8N/kg。
重力仅在垂直方向上起到作用,因此只改变了鸟在垂直方向上的运动。那么水平方向上呢?因为重力不改变鸟在水平方向上的运动,那么在水平方向上速度就保持恒定了。抛体运动经过这样分解为垂直方向与水平方向之后,就符合物理书里对抛体运动的描述,那么愤怒的小鸟TM的运动是这样的吗?
你如何测量小红在水平方向上运动?嗯,有多种方法供你参考。你可以使用屏幕捕捉工具或者在游戏视频前架设一个视频摄像头拍摄游戏过程。然后,你就可以清楚地观察到图像里小鸟在水平方向上每帧的移动情况;另一种方法也很有用——使用视频分析软件。正如我在前一章中给大家演示的,这种方法的基本思路是在视频的每一帧里标记好对象坐标位置,得到的x, y坐标数据与对应的时间数据。有很多的软件包都可以为你做到这一点,很多课堂上用于分析运动所使用的是一款Venier公司的Logger Pro(游标记录专业版)软件。我个人更喜欢免费的(更强大的)Doug Brown公司出品的Tracker Video(视频跟踪)软件。
根据视频软件的分析,小红在被弹射以后,在从图像的一帧跨到另一帧的过程中,水平方向上的位移均是相等的,或许你可以说水平方向上的速度是恒定不变的。
经视频进一步分析,小红的运动速度是每秒2.46“距离单位”。恩,什么是“距离单位”?这个“距离单位”并不是标准单位“米”。在游戏的情景下,这是愤怒的小鸟TM这一款游戏世界里专门使用的单位(我称为AB,而不是m)。在分析视频时,我要往软件里输入的是实际场景与游戏场景之间的比例尺,即屏幕上的每个像素对应真实世界的大小。但很遗憾,我无法确实真正的现实距离为多少,因此,我只能退而求其次,暂时将1个单位的AB定义为弹弓一次发射的长度。
可是,我还是不甘心,到底有没有什么方法可以让我把愤怒的小鸟TM游戏世界里的距离还原到真正世界里?答案是也许可以。让我从观察小红在垂直方向上的运动入手来试图破解这个难题。重力是作用在小红上唯一的恒力,这也决定了小红在垂直方向上的加速度是恒定的。恒定的垂直加速度意味着恒定的速度在垂直方向上的变化。如果速度不断地发生变化,反映在函数图上即是斜率不断地变大,那么在电脑上呈现的图形会是一个什么模样?答案是抛物线。下面这张图以时间为自变量,垂直方向的位移为因变量,斜率为速度,可以很好地展示小红这种特殊的运动形式:
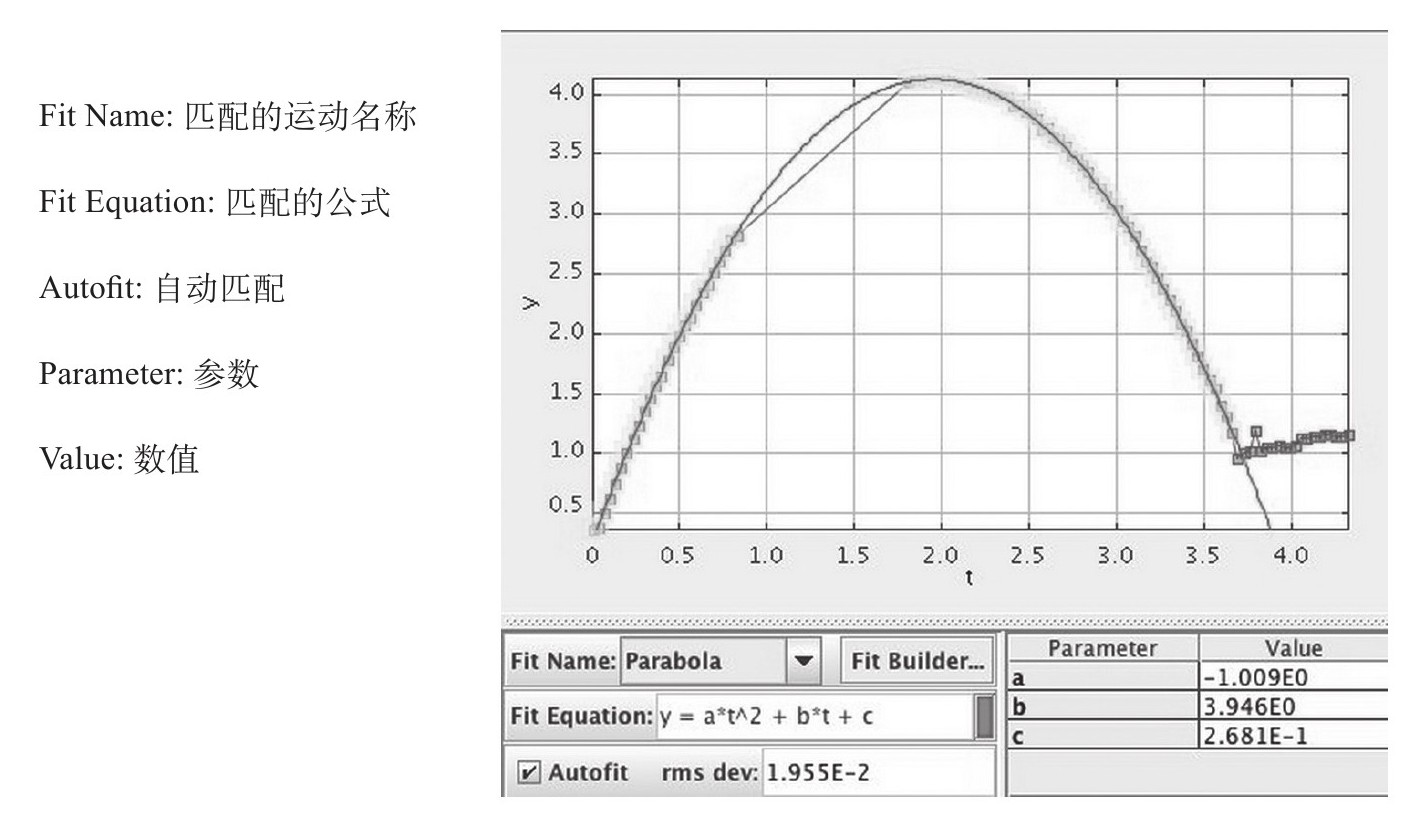
为了不打断我们研究的思路,该公式的推导从略,如果一个物体以恒定加速度运动,那么它的位移函数应如下:
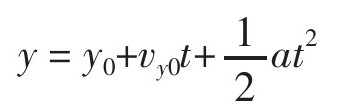
幸好Tracker Video兼容了抛物线函数的数据,所以我可以看到在t2前的数值显示为a=-1.0AB/s2(请记住AB是愤怒的小鸟TM世界里的长度单位)。这样,根据函数反推小鸟在垂直方向上的加速度是-2AB/s2。
这个计算加速度的技巧实在是再神奇不过了!如果我认为愤怒的小鸟TM这款游戏真实地发生在地球上,又会怎么样?在这种假设下,小鸟仅受重力作用的影响,垂直方向的加速度应为-9.8m/s2。垂直方向的运动把游戏里和游戏外的世界联系起来了,我因此就可以很方便地把这两个值设置为相等,我于是可以很顺利地得到AB和长度单位之间的比例关系。简单的转换以后我得到1AB=4.9m,根据一开始把AB定义为弹弓的射程,于是弹弓射击的高度在现实世界里应该近5m。那么小红呢?使用相同的比例尺,小红的高度为70cm左右。经过这么一计算,我们才知道这原来是一种体型巨大的鸟,一只超大的愤怒的鸟。
让我们再来看另外一种鸟:蓝鸟。这种蓝色鸟类也需要一个别称,我就简易地称它为小蓝。小蓝身怀绝技,如果你对它还不熟悉,那你必须先了解一下小蓝的特殊本领——在空中一分为三。这种能力实在是强大无比啊。除了这项本领以外,蓝鸟比任何其他的鸟类更善于打破玻璃结构的猪棚。
这里就有一个问题出现了:小蓝一分为三的时候,质量上发生了什么变化?分出的新鸟的质量是原来大鸟的三分之一?也许不是的,会不会每只新产生的蓝鸟具有和原来相同的质量?(这说明愤怒的小鸟TM游戏世界里的质量并不守恒)
刚才我们通过重力加速度巧妙地解决了长度的问题,现在我开始着手质量的问题,那么我将如何测量愤怒的小鸟TM游戏世界里的质量?我有没有一个可供参考的比例尺?没有,不过那也没关系。对我的研究而言,愤怒的小鸟TM这款游戏的有趣之处就在这里——你想尝试回答一个问题,但你找不到任何切入点,你必须拿出一些替代性的实验证据。这种有趣的挑战正是你在实际的科学工作里会遇到的。
让我举一个真实的例子加以说明我的上述观点。假设你要测量像电子一般大小的微粒质量,你能不能准备一台秤,然后就按部就班地进入下一步骤?不,当然不行啊。相反,你必须找到一些其他的方式来确定质量。事实上,对于这种情况,可以首先为带电粒子确定质荷比,然后追加另外一个实验来最终确定电荷的质量。诚然,过程很复杂,但我知道那就是科学开展的正确方式,就是科学能带来如此多乐趣的原因。设想如果攀登珠穆朗玛峰对于登山者来说不费吹灰之力,那还有多少登山者会乐此不疲,因攀登而觉得有趣?没错,假如做某件事轻而易举情况会完全不一样。
重新回到愤怒的小鸟TM。我们如何调查质量?有什么运动和质量相关吗?我马上想到的就是游戏里面的碰撞。好吧,我们首先来学习一下碰撞。假设我有两个物体发生相互作用(A物体和B物体),在相互作用的过程中,A物体推动了B物体,B物体也反推了A物体,这两个力大小相同,但其力的大小跟各自拥有的质量是无关的。
所以力是相同的(力是矢量,当然指的是大小上的一样)。但到底力做了什么呢?力改变了动量。关于动量,有两个重要的因素需要我们牢记(有很多关于动量的知识需要学习,我可以花一整个学期来教授动量):动量是质量和速度的乘积。动量也是矢量(动量有方向)。
在碰撞时,两个质量块具有相同的力,发生相互作用力的时间也相同。它们的动量改变量相同(但方向相反)。不要忘了“改变量”这个术语,这一点至关重要。这个问题的关键是,如果假设动量守恒,我可以根据速率的变化推导出质量。
现在,为愤怒的小鸟TM做一个实验。我需要做的是找准游戏里的一关,这一关力的任务正好可以让我为蓝鸟找到一个合适的撞击目标。如果你仔细观察,会发现游戏里有一关的场景是这样的:一块短板上放着一块岩石。例如,愤怒的小鸟TM原版的3-3关里就有这么一个游戏场景设置,这块放在短板上的石头看上去有点像一个支架上放了一颗软式垒球。我可以用小蓝来射击这块石头,并使用视频分析软件来测量鸟和岩石碰撞后的速度。
通过测量碰撞后的物体的速度,我可以得到物体的质量比(假设动量守恒)。为了进行比较,让我先分析小红。我展示一下我是如何得出碰撞前后速率之比的。
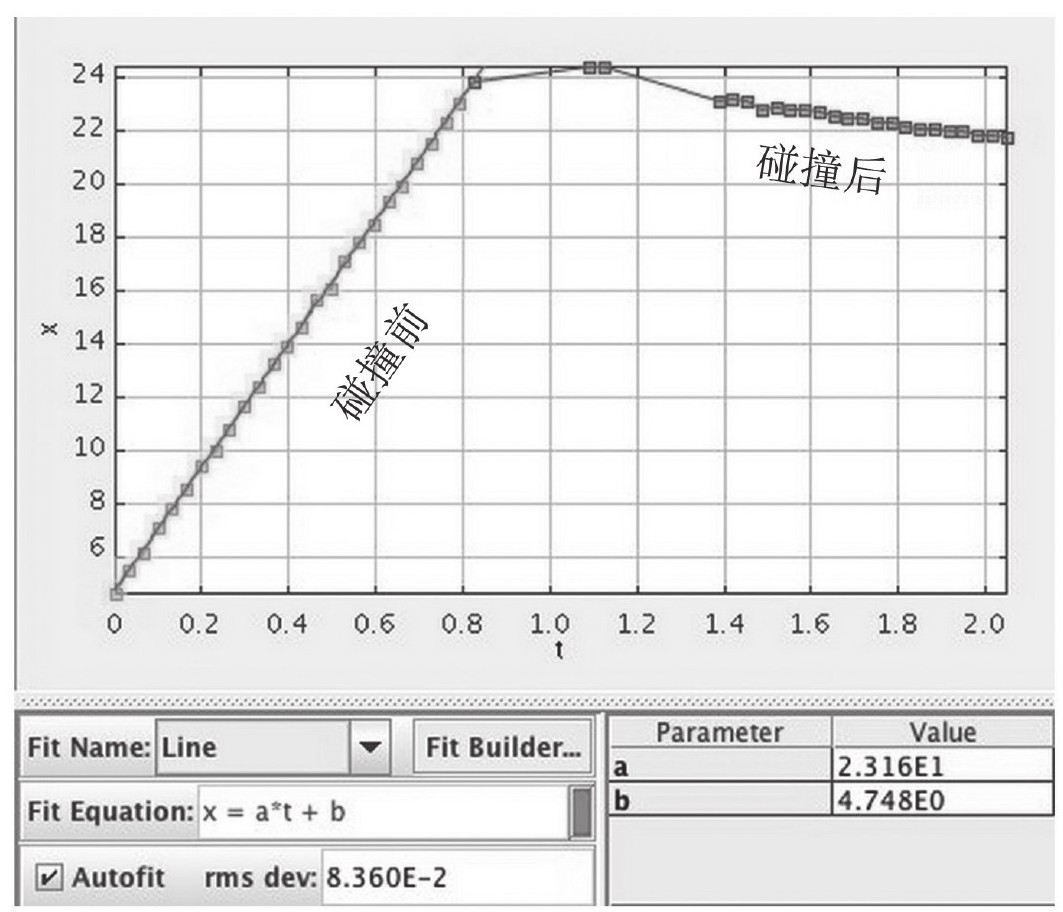
这是在水平方向上的速度图形。碰撞发生(至少是相互作用力)在x方向,所以我并不真正需要担心的其实是垂直(y方向)运动。这样是合适的,因为由于重力,动量不会在垂直方向上守恒。
得出小红在碰撞前后的速度之后,我可以用同样的方式求解出岩石在碰撞后的速度。如果动量守恒那么小红的质量为岩石质量的0.31倍。是的,请原谅我在这里省却了许多代数计算的细节。也许我应该把小红的质量作为愤怒的小鸟TM里质量的标准单位。那么在这种设定下,我设置小红的质量是1mr(其中,mr是愤怒的小鸟的质量单位,代表小红的质量),岩石的质量就是3.1mr。鉴于游戏里面根本找不到愤怒的小鸟和现实中的小鸟之间的任何质量上的联系,为了破解这一难题,这已经是我能做到的极限了。
那么小蓝呢?在这里,我需要做两件事情。首先,在小蓝不分为3只鸟的前提下,我将用它来打击同一块岩石。之后,我把小蓝分为3只新鸟,使这3只中的一只再去击打岩石。
在一只小蓝(未经过分解)撞击岩石后,我发现它的质量是小红的质量的0.019倍(0.019mr)。多么小的一只雏鸟,小红的质量是它的60倍。
现在,我把小蓝分为3只新鸟,使这3只中的一只再去击打岩石,我也可以得到它的质量。经过计算,我发现它的质量为0.29mr。
这很奇怪,不是吗?这个新生的蓝鸟倒比原来的那只大了15倍。如果你把所有3只新生的蓝色小鸟的质量加在一起,总质量会是原始质量的45倍。坦率地说,我有点惊讶。我起初的想法是新生的蓝鸟可能会和原来的那只质量一样。这样的结果就大大超过我的预料了。
好了,我该如何去解释这种不遵守质量守恒定律的物理现象呢?是的,我知道这只不过是一个视频游戏罢了,又不是真实生活的世界,何必如此认真呢?但我还是想尝试着用物理知识去验证游戏世界是不是运用着一套和我们现实世界相同的物理法则。对此,第一种解释是愤怒的小鸟TM里动量是不守恒的。为什么要守恒呢?它不必和我们生活的世界遵循相同的规则,对吧?第二个解释是,当你点击屏幕,你就等于敲开了一个全新世界的大门,原来的小蓝分身进入了这个新世界。这些新鸟只是看起来像以前的小蓝,但它们已经脱胎换骨,摇身一变成了用金属钛或其他什么材料打造的新鸟了。
这说明什么呢?这说明通过“经过碰撞过的”小蓝你可以在游戏里面获得极大的优势。如果游戏时冷落了小蓝,不善加以使用,那就有点不划算了。记得送它去另一个世界。
在继续研究黄色小鸟的物理现象之前,也许我们应该停下来先读一首日本俳句:
太阳当空照,绿豕尾巴翘着笑,木板顶头断。
哦,当然,俳句用什么样的的形式是个仁者见仁的话题,但对于黄色的鸟有什么本领大家的意见是统一的,没有争论。首先,黄鸟可以比大多数鸟类更好地粉碎木头。第二,当你在黄鸟运动的时候点击屏幕,会出现变化,到底发生了什么变化呢?
我多年以前第一次开始玩愤怒的小鸟TM的时候,第一个感觉就是点击屏幕后黄鸟的速度会保持不变。后来有一天,我不小心把黄鸟打得过高了,结果它的高度没有不断上升,看上去简直就像一条抛物线。我这会儿才意识到我一开始的感觉出了问题。下一步该怎么做?收集数据。
点击黄鸟之前,它有一定的速度。显然,点击后它的速度不同了。也许在黄鸟飞行的方向上点击产生了一个加速度,使得它不断地朝着一个方向运动。
视频分析之后,你可以更深入地了解黄鸟在点击前后发生的变化。经过计算机软件作图后,我发现无论是水平方向还是和垂直方向上点击后的速度都提升了。此外,在水平方向上是没有加速的(仅在短时的点击瞬间才有)。对于垂直方向的运动而言,在非点击时间段里的加速似乎是恒定的,整个过程因此就像个纯粹的抛物线运动。
但在点击过程中具体发生了什么还是不明确。如果你再多观察几次不同的黄鸟的射击并加以纪录,有一点会很清楚:点击的效果持续时间为0.067s,在这么短的一段时间里,加速度在发生变化,x和y方向上速度也随之产生变化了。
几次射击过后,所有的这些射击造成的加速度都是不一致的,看上去加速度几乎是在每次都是随机不断在调整的,但是不管怎样,加速度目的只有一个——黄鸟的速度在点击后达到30m/s。
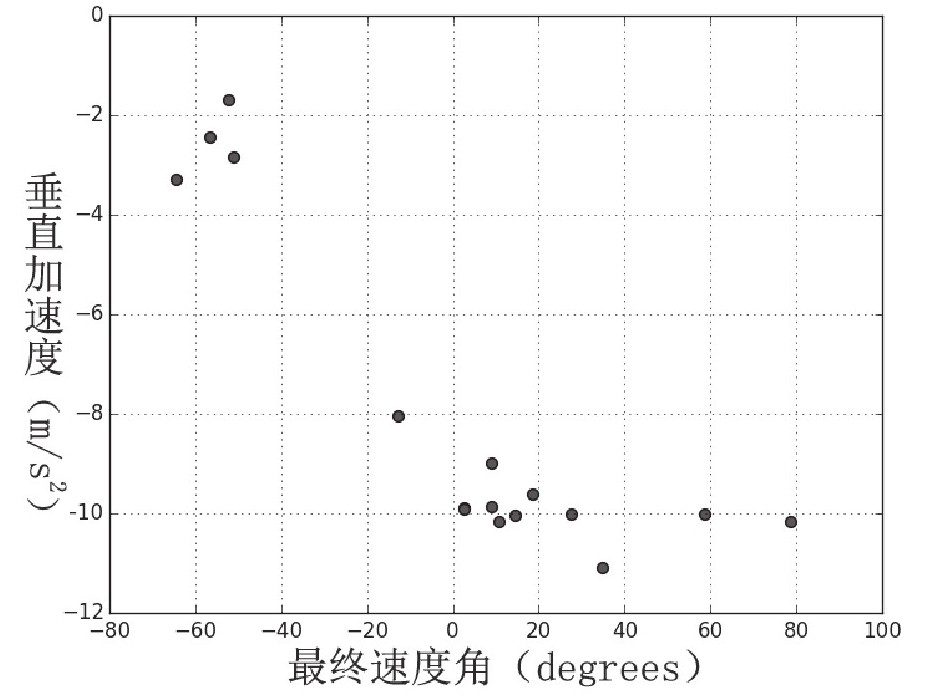
请注意,我用的是“几乎”一词,因为实际上最终速度也并不总是30m/s。在某些情况下很奇怪,黄鸟的行为在点击后会变得十分异常。比如,如果黄鸟已经处于下降过程中,你再点击,它的垂直加速度就不是原来那个值了。下面这幅图说明的正是在点击后垂直方向的加速度和黄鸟移动时与地平线角度之间的关系:
请注意,大多数鸟的加速度约为-9.8m/s2,和你预想的一样。然而,正如图所示,如果鸟运动的时候向下与水平方向构成大约50~60°时,垂直加速度只有大约-3m/s2左右。这种现象颇让人费解。也许游戏开发商认为如果小鸟的飞行角度太陡,黄鸟最终会飞行得过快。毕竟,这是他们发明的游戏,规则自然也只由他们来制定。
到这里,愤怒的小鸟TM这款游戏的“物理学”规律终于水落石出了。我想有时候,我们探索得到的答案是明确的,但也有时候,我们苦苦地探索,换来的只是更多的命题,但后者对于科学更有意义。
