让我先从一个小测验的问题开始。
在《星球大战II:克隆人的进攻》里,R2-D2展现了他飞翔的能力。R2-D2会飞,有什么不对的吗?对于这个问题,可能的答案如下:
(1)没有。乔治·卢卡斯的本意就是让他在《星球大战》的一开始就大显身手一番,可惜当时用Commodore64号计算机不能制作R2这种数码飞行的特效,所以只能作罢。
(2)如果R2能飞,为什么原来的三部曲里面不见他飞呢?
(3)他不会以那种方式飞。
(4)机器人不应被允许飞行。
这里,你看(1)这个选项很容易让人上当。为什么(1)不对?因为Commodore64直到1982年才发行,《星球大战》电影(那时候《星球大战》还只是被称为《星球大战》)最早发行年代是1977年,所以(1)答案肯定不是正确的。
正确答案是(3):R2-D2不会以那种方式飞。

不以那种方式飞,那他是怎么飞的呢?如果你仔细看电影,你会发现虽然R2(所有和他的关系很铁的朋友都叫他R2而不是R2-D2——他的全名)在飞行的时候,他的推进器并不是和行进方向在一条直线上的,推进器是倾斜的,一半向后伸,一半往下降。下面这张图用另外一个机器人来模拟R2-D2飞行方式:
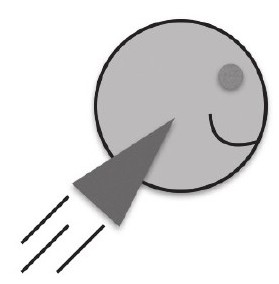
这就是R2以一个恒定速度飞行时的方式。你可能会想:咦,这有什么不对的呢?看起来丝毫没有问题啊!但我觉得这才是真正的问题。R2的飞行方式是按照大多数人对于力量与运动的思考来进行的,所以没有人会认为这里面有问题。
啊,但现在我们正在谈论的就是力和运动。让我以这一领域里的两位专家来引入我们的讨论:亚里士多德和艾萨克·牛顿。
亚里士多德对于力和运动有什么见解?对他来说,恒力是维持物体不断运动的原因。说实话,对于大多数人来说,这样的想法是很有道理的。即使亚里士多德讲的是希腊语,很多人也会认同他。这样的想法在现实中不是得到了印证吗?如果我在桌面上移动一,这动起来了,如果我加大我的推力,它动起来的速度就更快了。如果我停下来不再推,这也将停止运动。这种想法很简单明了。
根据亚里士多德,R2-D2应该以上述方式飞行。要以恒定的速度飞行,他需要把推进器的角度向后调整一下。这样一来,推进器的一部分可以在后面给予一个向上的推进力,让他免于下坠,另外一部分可以给予一个向前的推进力支持他水平飞行。
现在,牛顿呢?关于力和运动的更完备的理论不只是牛顿个人提出来的。只不过人们把这些理论一律归结在牛顿运动定理的“账”下。牛顿说,力是改变物体运动状态的原因。关键词是“改变”。如果对一个物体施加一个恒力,它会持续改变其运动。这也就是说在一个恒力的作用下物体的速度会不断攀升。
考虑下面这个例子。保龄球静止地停在光滑的保龄球道上。如果你轻轻一推,它就开始移动,继续滚动一段时间,但最终会停止。这是因为球道在保龄球上施加了一个大多数人都会忘记的一个力:摩擦力。因此推球后,使球慢下来只有这个力。但是,如果你在球后面追着它不断地推它着跑,你可以以很小的一点推力使它以匀速继续运动下去,因为你的推力正是起到了平衡摩擦力的作用。如果使用长棒,施加一个比摩擦力更大的持续力,球的运动速度会越来越快。
假设有一个方法可以从一个移动物体上移除所有的力。对于这样的一个物体,速度将保持不变。我知道这很难想象,因为我们在地球上看到的一切物体都受到某种摩擦力的影响。
好吧,如果你看一下R2飞行的方式,这种方式和亚里士多德或者90%的人的想法是不默而合的。但有没有什么办法,可以使这个R2-D2的飞行方式和牛顿运动定律相一致呢?换句话说,在什么情况下,这种飞行方式符合牛顿物理学?
空气阻力就是我们在这个时候的最佳选择。假设R2飞行空气阻力是不可忽略的。在这种情况下,他就必须调整一下推进器的角度,让它与飞行器成一直线的方向上偏离一点,起到平衡水平方向上空气阻力的作用。实际上,我们可以根据这种关系计算出R2的重量。其过程为:假设已知空气阻力与它飞行的速度,计算出用于推进的推力也不在话下了。如果知道推力有多大,我们就可以方便地算出推力在竖直方向上提起他的力的大小。如果我画一张R2的受力分析图,应该是这样的:
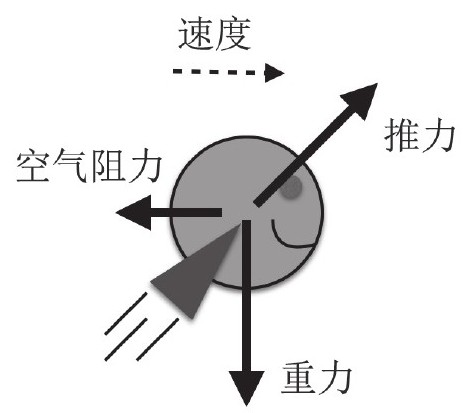
如果我能模拟算出空气阻力的大小,我就可以估算出推力进而得到R2的重量。
首先,做一些假设:
●我将假设存在类似于地心引力的引力场。为什么这么做呢?为什么不?如果你看看人物在电影里面是如何活蹦乱跳的,你就会明白他们好像就是在地球上(他们确实是在地球上)。
●存在类似地球上的空气的环境。这个有点难以自圆其说了。我怎么知道空气是不是超密度的?或相反密度非常低?我不知道。但因为我没有太多的选择,权宜之计下,我只好假设这颗星球上的空气和地球上的空气密度一样。
●对于这种具体的情况,我也将使用2.3m/s这个速度。这就不是一个假设了。通过使用视频分析,我绘制了一张R2在不同时刻位于不同位置的的坐标图,我再把不同位置与时间连成一条直线。这条直线的斜率就是速度。
●该推进器角度与R2的角度约为43°。这也是从视频里测量得到的。
●最后,我将必须对R2-D2的物理尺寸做出估计。
接下来我的事情就是评估一下空气阻力的大小。对于低速运动的物体(像这样的)空气阻力与速度的平方、物体的大小和形状、空气的密度成正比。有了这些估值,每一个R2的单元质量大约为100g,这使得他的密度跟空气自身的密度所差无几了。如果密度这么低,他会飘浮起来。说真的,他甚至不需要用什么向上调整推进器来抵消空去阻力。
最后,R2-D2不可能那么轻。他只是飞行的方式错了而已。
