是否有可能建立一架人力驱动的直升机盘旋于空中?嗯,是的,有可能。有一个马里兰大学GameraII项目就成功做到了。这架人力驱动的直升机成功地在空中盘旋了约50秒的时间。好奇的观众很可能会马上问这样一个问题:要完成这个项目有多难?
直升机的操作是很不容易的。你有没有见过在直升机上的那些控制按钮?它们的复杂程度足以令人望而却步。但是,某个事物异常复杂并不意味着我们就不能为之创造出一个简单化的模型来分析它。我想要分析一下的正是直升机在空中悬停需要多少能量。

我们从最基本的原理说起。一架直升机能悬停在空中是因为它向下“抛出”空气。火箭用的也几乎是一模一样的工作原理,只不过火箭自身并没有携带任何空气。如果你想向下“抛球”,你必须用力拍球,同时球也会向你回弹。如果你用手拍球的力度足够大,在球给你的回弹力的作用下,你就可能离开地面。当然,如果使劲推球,回弹到你手中的球又会马上脱离你的手。如果你开过枪,感觉过射击时的后座力,你就会明白这个道理——开枪之后子弹以难以置信的高速从枪膛射出,形成一个与子弹方向相反的后座力。
同理,直升机也通过向下不断“抛球”来解决这个悬停的力的问题,只不过对于直升机来说,现在的“球”变成了空气。
让我们为这个向下“抛空气”的直升机建立一个模型,假设直升机的螺旋桨下排的空气形成了一个圆柱体的空气结构,空气的最终速度是v。我可以简单地了解到这个气柱的长度,然后根据空气密度(大约1.2kg/m3)计算出空气的质量。如果空气的初始状态是静止的,那么要把空气的速度增加到v所需力的大小就取决于这段加速时间的长短。
由于该空气柱的长度取决于速度和时间,我可以给出一个只由“推速”决定的力的表达式。
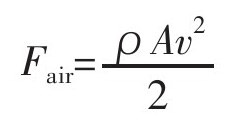
这里ρ表示空气密度,A为螺旋桨转起来扫过的面积(就是被向下排的空气柱的横截面积),v是向下排的空气的速度(就是我刚才说的“推速”)。为什么“2”会出现在分母部位?这是因为我假定空气开始时静止,加速到v,整个过程的空气柱平均速度就是v/2。
如果你对这个公式不放心想查验一下。你看一下,该公式的计算结果是牛顿,即力大小的单位,恰是施加到空气上的力的单位。此外,如果增加螺旋桨的尺寸或者空气被下排的速度,所得结果也会相应增加。这些结果都从侧面验证了这个公式的正确性。反过来,如果速度增加,算出来的力大小减少,那就不对了,是吧?
根据牛顿第三定律,这个力在大小上必须能够支撑整个直升机。这个论断是很重要的一个条件。如果已知直升机的质量和螺旋桨的尺寸,我就可以算出空气“推速”的大小了。
直升机的功率需要达到多少?如果你还记得,功率指的是物体在单位时间内所做的功的大小。在此例中,直升机所做的功就是不断使得空气圆柱的速度从零增加到“推速”过程中的动能,中间所花的时间则由空气的速度决定。将这些量放在一起,我得出了一个直升机能在空中悬停的所需功率的数学表达式:
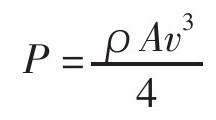
请记住,这仅仅是悬停所需的功率,它并没有把地面效应纳入考虑,也忽略了直升机在空中的向前运动或者其他因素。但你怎么才能判断一个模型是否合理?我把这个模型用到真正的直升机上去试验一下如何?如果你查看一下维基百科,你可以找到很多有用的直升机数据。我找到了直升机各种各样的数据,包括:质量、螺旋桨的尺寸和发动机功率等。
鉴于推速可以根据螺旋桨的尺寸和飞机的质量来计算,我可以用这两个量来得出一个直升机悬停所需的功率。这是我的计算得到悬停功率(y轴)与实际在维基百科上列出的真实的直升机发动机功率(x轴)之间的对比图:
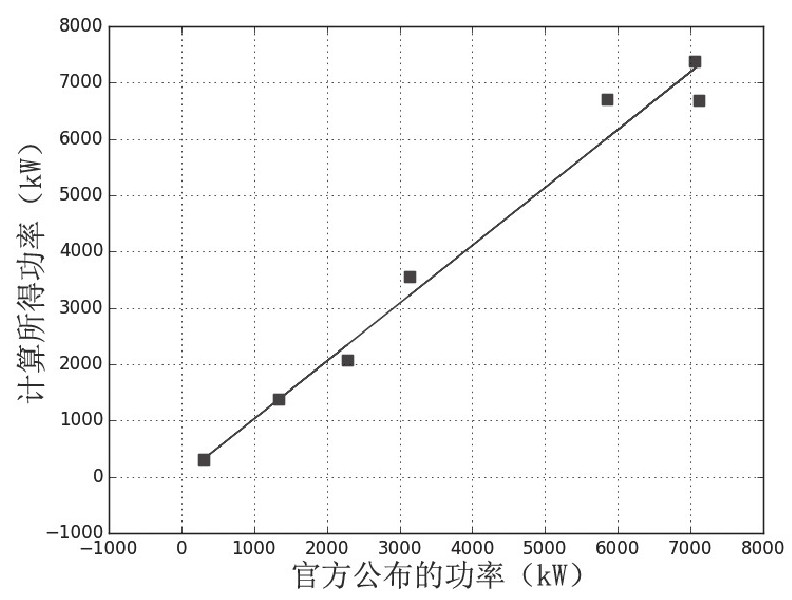
显然,整个图看起来具有相当线性,不是吗?这就说明我建立的直升机悬停功率模型并没有和实际偏离得很远。而且,我还发现,关于维基百科上直升机的真实数据还有一个相当有趣的地方:假如你按质量和空气“推速v”来做图,两者之间你会根本找不到任何相关性。因为事实上,所有现实的直升机的“推速v”大约都在28m/s左右。根据上述公式来看,这就意味着直升机越大,质量越大,只有增长螺旋桨才能维持一个较大的功率供给,因为空气被向下排的速度即“推速”基本上都维持在恒定的28m/s。
那么,我们如何使用我们已知的这些物理知识来建造一架人力驱动的直升机呢?首先,让我们先来分析一下GameraII项目的实测数据。这架人力驱动的直升机(或者干脆就叫它人力直升机)质量为32kg,有4个螺旋桨,每个半径为6.5m。对于飞行员的的质量,取60kg为宜。我建议你去看看拍摄这架直升机时的镜头,我这里先把要点总结给你:首先,4个约12m长的螺旋桨就意味着要占据一个很大的空间,看上去就像用农具做成的一把用在池塘上的大网勺一样,而且重量也得出奇得轻;此外,飞行50s便能在室内离开地板,在理想条件下悬停一分钟不到。这样如同鸡肋般的效果,恐怕詹姆斯·邦德或蝙蝠侠都是不会觉得有什么用处的。
大型的螺旋桨对直升机意义也很大。螺旋桨扫过的面积大、功率一定时,空气“推速”就可以低得多。第二个表达式有两个因素对功率产生影响:螺旋桨的尺寸和“推速v”。进一步分析这个公式的数学特性,我们可以看出:功率P和螺旋桨扫过的面积A成直接正比关系,但和“推速v”的三次方成正比。如果你把“推速v”加倍,功率就增加8倍,而面积加倍,功率也只是一样加倍。因此,要尽量降低制造的难度,螺旋桨要尽可能的大而轻,这样对于由人力维持的“推速”的要求就可以减轻。
如果我使用这些GameraII项目里的数值代入到第一个、第二个公式来计算所需要的“推速v”,我得到结果是1.68m/s,功率P为755W,比一个马力稍高。虽然这已经是一个相当高的功率要求,但也并非高到人力所至的范围之外。根据维基百科的描述,优秀的自行车运动员的功率输出可以以2000W维持很短一段时间。755W自然也不轻松,但还是有可能做到的。另外,这人力直升机的飞行员是手脚并用的,他的手和脚同时在曲轴上做功。根据我们的计算这个项目是可以成功完成的。
我不得不指出,整架项目制造出来的带有4个大螺旋桨的人力直升机看起来颇有点像神盾局里的“天空航母”。“天空航母”是什么?在《复仇者联盟》里面,有一艘叫“天空航母”的航空母舰,飞起来也是用4个巨型螺旋桨。那么,现实中运用这样的设计能成功吗?这个飞行器能悬停于空中吗?让我先以一些假设入手来解答这个问题。
●我只会采用《复仇者联盟》里面那个天空航母的样式。在漫画里面,它还有其他的样式。
●不存在特殊的空气动力学效应的问题,如地面效应,来协助天空航母悬停。直升机近地而飞,对于能量的需求其实并不大。这是因为,螺旋桨下排的空气和地面产生相互作用,反过来又和直升机产生相互作用,这就形成了所谓的地面效应。
●在电影里的“天空航母”的大小和质量和一个真正的航母所差无几。
●该“天空航母”在螺旋桨的气流作用下悬停,它并不像一架质量轻于空气、处于漂浮状态的飞行器。我想这和我在电影场景看到的情况不谋而合,因为电影的拍摄者所展示的“天空航母”就是放在水上的,和一架普通的航母一样浮在水面上。
如果“天空航母”和尼米兹级航母有一样的长度和质量,那么查到的资料显示它的质量约108kg,长度333m,螺旋桨面积将达到4000m2。
运用同样的模型,我可以把这些值代入前面的公式来估算出航母所需的“推速”。经计算,速度是640m/s。需要澄清一下,这个速度比声速更快,虽然还比不上航天飞机上固体火箭助推器里的气体速度。从固体火箭助推器里出来的火箭燃气一般具有5000~10000英里的时速。你可以明白螺旋桨太小就会出问题的原因了。为了保持飞行状态,需要很大的推速。请记住,真正的直升机的推速在30m/s以下。
功率的问题怎么办?这又是另一个问题。极高的推速对功率要求非常高。在上述情况下,悬停所需的功率是3.17×1011W(4.26×108马力)。这个马力已经相当大了,需要很多“马”来开拉。相比之下,尼米兹级航母的推动功率官方公布的数据是1.94×108W。我认为这已经是功率的极大值了,但还不足以让“天空航母”离开地面。显然,神盾局一定为天空航母制造了更优良的能源供给系统,我想操控天空航母必须至少具备2×109W的功率,因为最大功率如果还不足以使航母动起来那就等于坐以待毙了。
如果我想改造一下神盾局的天空航母呢?让螺旋桨的气流推速为50m/s(这个速度比普通的直升机还要大一点)?在这种情况下,螺旋桨扫过的面积将达到650000m2。螺旋桨将从18米的半径(如在电影中所见)一下扩展到220多米。没错,光想象画面就觉得很有趣。
我们何妨换一个角度来思考呢?如果螺旋桨的大小真如电影里所示,能升起多大的重量?使用相同的计算方法,求解出重量为600000kg。这大约是100英尺长的一艘拖船的质量。一个只有拖船大小的天空航母就不会那么让人惊叹了。
最后,要用人力驱动直升机,看起来是困难重重,却是有可能的。之所以具有可能性,是因为别人已经做到了。如果你自己想用直升机的螺旋桨来制造一个大型的飞行器,最好还是能配备一个大型的电源或非常大的螺旋桨。
