如果你从未见过一把扫帚直立不倒,那么我可以告诉你,一把扫帚完全可以站立起来。在派对聚会上你可以大显身手,放开手,让它竖直站立在地面之上。随之而来,旁观者会这样说到:
哦,今天十字连星,是个特别的日子,你才可以让一把扫帚保持平衡,直立不倒!

今天也许确实是个特殊的日子(这个派对是为了庆祝你的生日或者别的什么),但行星的位置对于任何事情其实是起不了任何作用的。
让我从重力入手。这里重力可不是你爸爸讲的“质量乘以g”得出的那个重力。我要讲的是真正的引力——牛顿引力(除非你的爸爸恰好是牛顿,那他说的才是我们要讲)。万有引力是物体之间因质量而产生的相互作用,它不仅仅是物体与地球之间的相互作用,因为这种相互作用只是两个物体间发生的最为显著的相互作用中的一例而已。假设我有2个物体,一个质量M1另一个质量为m2,两者之间的距离间隔为r(由质心之间实测得出),那么两者之间的万有引力的大小是:
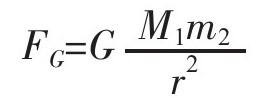
M1、m2表示物体的质量,G是引力常数,值为6.67×10-11N·m2/kg2。对不起,我不得不把那个数字写下来,要知道这个数值是非常之小的。
扫帚呢?扫帚的质量我估计是1kg,这个重要的数值后面会用到。什么物体在与这把扫帚产生相互作用?显然,那是地球,地球的质量大约为6×1024kg,而扫帚距离地球的球心大约为6000km(地球的半径)。既然我已经了解了所有的数值,现在我就把这些值代入到这个万有引力公式里,我最后经计算得到重力为9.8N(我故意为质量和地球半径取个整数值)。现在你终于知道为什么有一个“质量和g之间的乘积”这一公式了吧?因为它算出来与万有引力正好是一致的,也就是说地球表面每kg物体受到的地心引力为9.8N,9.8N/kg即来自于此,地球表面的物体都可以用“质量和g之间的乘积”这个算法来简单算出所受到的重力大小。
现在,那行星的问题又该如何解释呢?此刻,金星在夜空中正闪闪发亮,但它离我们有多远?用上互联网的方式来解答这个问题真是再好不过了,我建议使用wolframalpha这个网站,因为该网站提供给我们金星的质量以及我们和金星之间的距离。使用这两个值来取代刚才代入公式里的地球质量和物体距离地球球心之间的距离,我们算得万有引力为2×10-8N。与地球的引力相比,这个力确实是很小的。为什么会这样?原因出在距离,虽然金星的质量和地球的质量非常相似,但两者在距离上实在是相去甚远。
那换另一个不同的星球呢?我们也有类似木星这样质量大一点的星球啊?木星的质量约为金星质量的1000倍,当然距离上则更为遥不可及了。
根据它的质量和距离,最终我计算出的引力为2×10-7N。这个力还是跟刚才那个一样也微乎其微。
让我们再换一个对象来加以研究。你和扫帚之间的引力是多少?假设你的体重为65kg,身体的重心和扫帚的质心之间距离为0.3m,这将产生一个4.8×10-8N的引力。是的,这也是很小的力。但是,这个力显然比你和金星之间的引力要更大一些。所以这便是你该有的答案——就连在扫帚周围走的人都可以和扫帚之间产生一个引力,而且这个引力和行星与扫帚之间的引力在大小上还相差无几(或许还是人和扫帚之间的引力大一点呢),那么就算十字连星又能怎么样呢?
还是回到这个问题,假如不是由于行星的引力让你把扫帚直立起来的话,你又是如何做到让扫帚平衡的?其实这并不困难。有十分重要的两点需要考虑的。首先,一把扫帚的质心是相当低的,其位置比许多人估计的还要更加接近地面,因为扫帚前部的刷件在扫帚底部,又比扫帚柄要来的宽大,所以整个扫帚的质心很低。
质心和平衡一把扫帚之间又有什么关系?如果扫帚的质心并不是位于对扫帚的某个支撑之上,那扫帚就要倾倒。因此,在这种情况下,扫帚的支撑区域已经被扫帚前部的刷件覆盖掉了;还有一点,也许是最重要的一点:刷件是会弯曲的,它像一个弹簧,具有回复力。这就意味着你不必在放手之前就非得让它平衡。你只需要靠近扫帚去尝试一下。一旦你让扫帚真的直立起来,你可以尝试去做另外一件异曲同工之妙的事:让一个鸡蛋直立。好不好直立与月球、太阳和行星一概无关。一年中任何一天只要你会小心翼翼地去做都是可以做到的。关键是要把鸡蛋玩转,这些鸡蛋蛋壳表面通常都有一些小疙瘩,恰恰可以被用来使鸡蛋直立起来。这件事看起来极酷,做起来也不像你听到的那么难。
平衡一个扫帚是个很酷、很好玩的游戏,但它不是由什么十字连星造成的。你不必相信别人告诉你的一切,有时候他们甚至不知道真相是什么。
