超人如此强大,天底下罕有什么事情他办不到,不是吗?那他能不能大手挥出一拳,把人打飞到太空里去?让我们通过一些估算来回答这个问题吧。
当我说到空间,你很可能会想到“外太空”。但这“外太空”的天到底有多高?包围在地球周围的大气层并不仅仅停留在某个高度就不存在了,它自上而下由密度不同的气层组成。事实上,高度越高空气的密度就越低,不断上升到后来大气层里的空气就会稀薄到荡然无存。就因为这个道理,我们需要选定一个我们能称之为“太空”的高度。我会挑地球表面以上420km处的位置为“太空”。为什么这个高度?而不是其他数值?因为420km是国际空间站的轨道高度,选这个高度是有理有据的。

一个人若要想直达太空得以多快的速度向着天空直行?我先申明,这就是文章一开始提出的超人挥出拳头痛击一个人之后的情形。当然,如果超人击中一个正常人,这人的躯体大概就难逃厄运了。为了避免这种问题发生,让我们首先假设超人打的是跟自己一模一样的克隆人,这个克隆人我在文章里称为“超人B”。当超人B飞起来的时候,只有两个作用于他身上的力——一个是会随着他高度不断上升而减少,但减少幅度不大的重力;另一个则是大气对超人B的空气阻力。一般的情况下,尤其是取近似值的时候,我们都把空气阻力忽略不计。要知道,也许在先前的一场战斗里,所有的空气早已经从地球被吸尽了,这是未为可知的。
如果我们要考察涉及位置变化的运动(从地球表面到420km高空),那么我们首选动能定理。动能定理告诉我们,对系统所做的功等于该系统能量的变化量。如果我把那个被打了的人(超人B)加上地球看作一个系统,那么系统之外就没有其他力对系统做功了(请记住,这是从超人挥拳之后),该系统的能量的变化量为0。在这种情况下,存在两种形式的能量:动能与重力势能。
我们尚不知道这个被打的人的初速度,但我们知道他的末速度。在运动轨迹的最高点,此人的瞬时速度为0,然后马上坠落下来,这也就意味着最后的动能也为零。那么重力势能的变化呢?对于两个相互作用的物体,重力势能与它们的质心之间的距离成反比,它也取决于两个物体的质量和万有引力常数。已知这些量,我就可以解决一个刚才不知道的量——那个人的初速度。
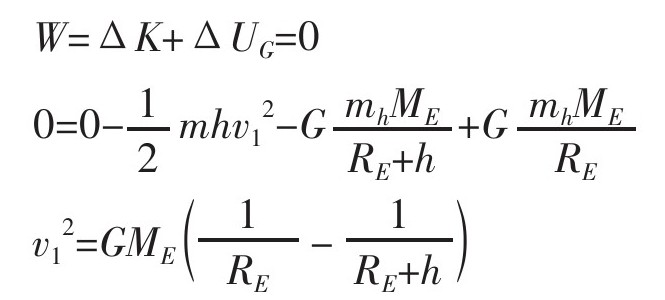
把所有已知量代入公式,那么我可以计算出他一开始的“发射”速度是2778m/s。是的,这个速度已经极快了,但超人B必须比这个速度还要快,为什么呢?有空气阻力,这就是原因。
这是超人B被击中后的受力分析:
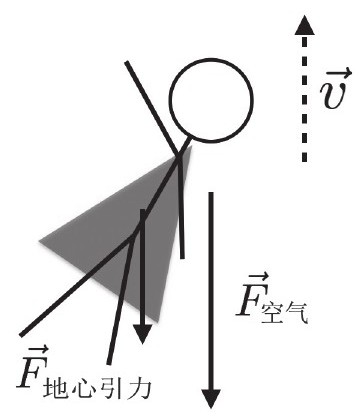
我用一下两个公式来得出重力的大小与空气阻力的大小:
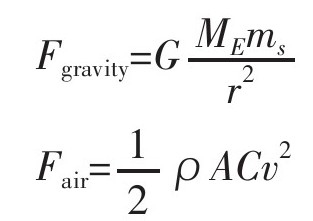
万有引力公式里包括地球的质量M和超人B的质量m, r是介于超人B和地心之间的距离。万有引力会随着超人B上升的高度而相应减少。
在空气阻力公式里,A是物体的横截面面积,C是阻力系数,取决于物体的形状。ρ是空气的密度,高度越高,密度将降低。正如你所知,空气阻力会随着速度和海拔高度而变化。事实上,阻力系数C也是取决于速度的,但我会暂且不考虑这个因素而认为这个阻力系数是恒定的。诚如你所见,如果再考虑阻力系数的变化,问题就不简单了。
我来做些估算,假设超人B和常人具有一样的身体尺寸和形态,质量相仿为70kg。假设有个跳伞运动员自由落体,那么阻力模型中AC的乘积就可以根据这位跳伞运动员的最终的速度v算得。如果一个跳伞运动员以54m/s的速度落下来,做匀速直线运动,合外力就为0,那么空气阻力就将等于该跳伞运动员最后的身体的重量。经计算,AC的乘积是0.392m2。在超人B这个案例中我取的是0.05m3的AC值。为什么呢?因为前面的计算考虑到的只是一个跳伞运动员以一般自由落体下落,超人B是以一个头朝天的位置被“发射”,他的横截面积将小得多,0.05的估值可能稍低,但是合理的。
另一个问题是处理空气密度的变化。幸好,我已经了解过高海拔地区的空气阻力问题——红牛斯特拉托斯太空跳伞开始的位置,空气密度比在地球表面的空气密度要低得多。在跳伞运动速度不断降低的过程中,我用下述曲线函数来表示这个密度变化的过程:
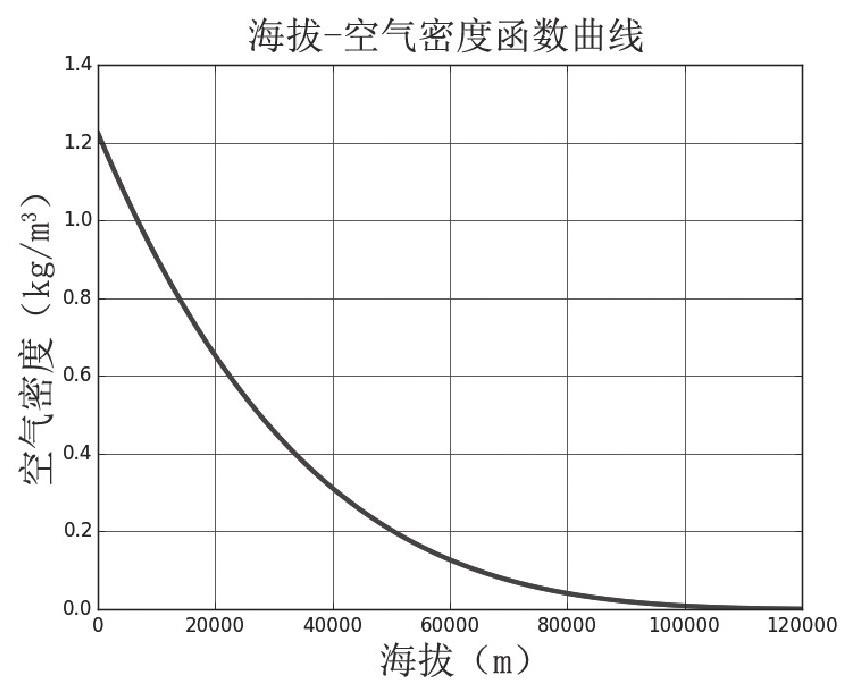
可见,这个模型对于海拔超高的情况并不适用。所以对这个模型,我使用的有效范围大概在100km,超过这个限值之后空气的密度忽略不计。是的,我知道这种忽略是不精确的,但它仍然可以帮助我们得出想要的结果。对于这项忽略,首先,我要表明超人B的初速度是非常大的,在高海拔忽略空气密度的条件下会使得计算出的初始速度偏小(因为实际上超人同时需要克服空气阻力);此外,当超人B到达到这些高海拔地区后,即便有一些空气,可由于密度很小,运行的速度再快,空气阻力仍然会很小。
现在怎么办?我不能直接计算出所需的初速度。不过我可以随意选择一个初速度,然后创建一个数学模型以确定超人B能到达的高度。然后,通过不断增加初速度,代入公式直到我得到我想要的高度。对于每一个初速度的选择,我会将整个运动过程分解为几个时间段。每一个时间段里,我将按部就班地完成:
●根据高度计算出空气的密度;
●通过高度、空气密度和速度分别计算出地心引力和空气阻力的大小;
●有了这个合力,计算出这段时间动量的变化;
●基于动量计算出这段时间高度的变化;
●重复上述步骤;
这些步骤看似复杂异常,但也不难完成。运用这个公式,我可以算出被击中的超人B以2778m/s的初速度能达到约海拔6500m的高空,但这甚至还没有摸到我们刚才划定好了的420km位置的“外太空”的边呢!
如果我继续增加速度来进行模拟,并结合空气阻力加以计算,那结果又将如何?最终速度如果足够高,是可以到达外太空的。这里我以初始速度为自变量(至105m/s为止),到达的最高海拔为因变量,绘制了一张两者的函数关系图:
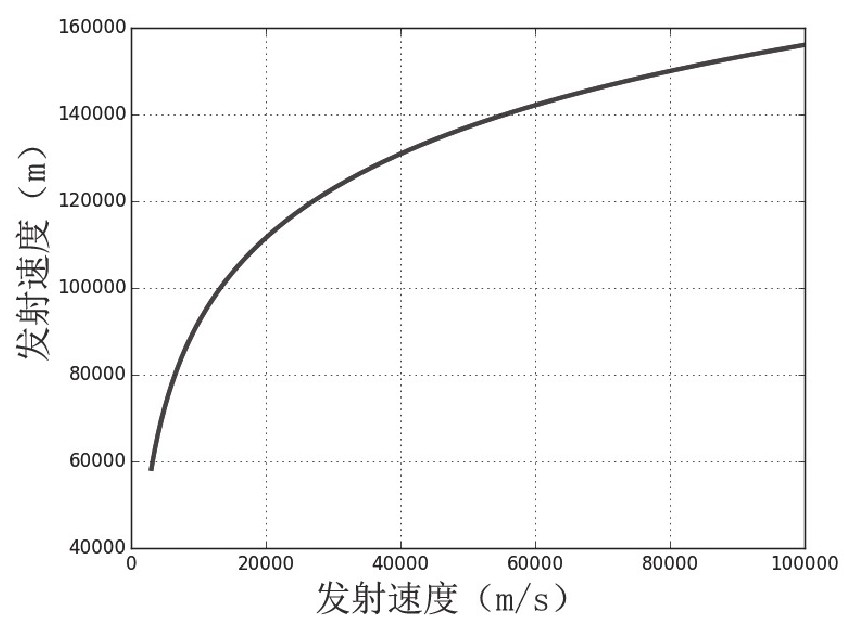
由图可见,即使在105m/s这样的高速,超人B只能到达大约13km的高度。对此,我本人也有点失望。我本来以为超人B应该可以到达一个高于这个海拔的高度。这样算下来,就算让超人在珠穆朗玛峰顶端挥拳痛击,也很难把超人B送入太空。可问题在于有空气阻力,为了抵消空气阻力做的那部分功,你需要给超人B一个更高的初速度。但是,如果初速度变大了,也就意味着空气阻力更大。一旦以一个超级速度启动,那么空气阻力模型也不成立了。
超人真的能把人打入外太空吗?也许可以吧,但那可不是简单的一拳。这事就算让超人来做,也有点儿麻烦。
但是,这一拳之击到底如何?比方说超人用尽全力向超人B挥拳一击,力量之大让超人B被打飞的最初一瞬间的速度到达105m/s,又会怎么样?会发生什么?比方说,一拳正好击中下巴——漂亮的一记曲臂挥拳上击,超人B被击中瞬间的受力分析为:
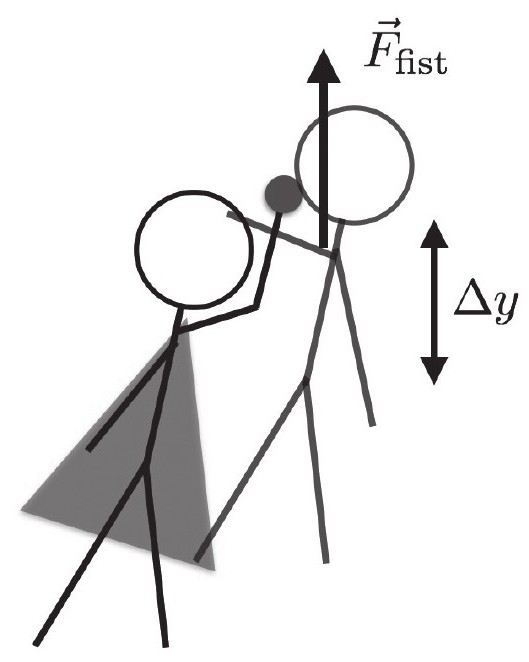
在这里,超人B进入太空的速度经过一段距离ΔY从0m/s陡然增加到105m/s。达到这样的效果,超人的打击力需要多大?我将忽略重力(重力效果这种情况下微乎其微),并使用动能定理。如果超人B是我的分析对象,那么只有超人能完成这个动作。为了计算功,需要拿超人拳头的力的大小去乘以位移距离。这个功产生了什么样结果?它改变了超人B的动能(它也改变了重力势能,但相对于动能的变化这个量是非常小的)。
如果我已知最终速度和挥拳的距离,我便可以计算出这一记超级拳力量大小的平均值。目前唯一没有估算的就是这记挥拳作用的力的距离是多大。我的估计是0.75m,这个数值对于这个动作而言是比较宽松、略大的。如此,最终力的平均值为4.67×1011N。
假设超人拳头的接触面积为70cm2(我测量了一下我的拳头的正面,得出这项估算,当然超人的拳头肯定更大一点),超人B的皮肤上会产生多大的压强?
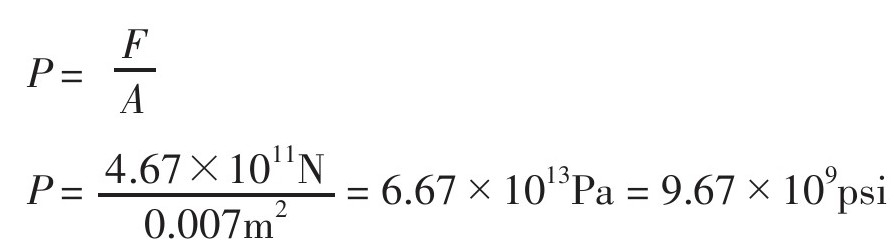
这是一个很高的压强。一个普通的潜水箱内部有3000psi的压强,一架钢制坦克的钢壁有0.75英寸厚。我这样说的目的何在?我此刻在想,如果超人可以以这样的强度去击打超人B,那这么一拳足以打穿头颅。我很清楚,这么说肯定让人感到不舒服。
那么超人的脚和地面之间的压强有多大呢?超人对地面的压力大致应该等于他打超人B拳头的力量。当然,他脚的接触面积比他的拳头的接触面积要大,但这个压强仍然是巨大的。我敢肯定拳头打出去的同时超人自己也会陷进地面。
这么大的力作用在超人B上,会有什么样的效果呢?如果超人B的体重为70kg,我就可以计算出他受到打击的过程中加速度的平均值,即力除以质量(对比而言,地心引力太小再次可以忽略不计)。经计算,平均加速度为6.67×109m/s2。
假想超人B是由两部分组成:头部质量为7kg,身体其他部分的质量为63kg。超人打的恰好是超人B的头,为什么他身体的其余部分也随之加速呢?当然了,头和身体是连在一起的嘛,超人B的头部通过脖子把整个身体连带拉起来。但为了使身体和头部一样获得加速度,则必须用4.2×1011N的力。
一尼米兹级航空母舰的重量约9×107kg。如果要产生上述大小的力,你可以把超人B头朝下脚朝上倒挂起来,然后在头部挂上4500艘航母。我无法断定你的头能否承受,但我认为他的头是肯定保不住了(还有,整个世界也拿不出4500艘航母来)。
综上所述,我们明确一点:超人没法送任何人上天。如果他真的使尽浑身力气动手打了某人,那么那个品尝他拳头滋味的人很可能头已不保了(模样也可能更加惨烈)。还有,如果超人打出这样力大无穷一计拳的同时,自己也该陷进地里去了。
也许超人就应该吹一口气,狂风乍起,一下就可以将人吹飞吧。
