我个人十分偏爱π这个数学符号,对于这点,我丝毫不隐瞒。连一个数学符号也喜欢?有什么特殊原因吗?我们来做一件有趣的事情,请你拿出计算器,把π这个值做平方,可以用计算器本身自带的π或者也可以取3.1415,或者任意一个计算器位数容得下的值。
计算完成了吗?有没有觉得这个值看起来很眼熟——π的平方是9.869,看起来正好和牛顿力学里讲的地球表面重力场内每千克物体所受到的地心引力值g很接近,这下你发现什么了吗?
且慢,到底你说的重力场是什么意思?由地心引力引起的9.8,难道单位不是m/s2吗?说的没错。很多人是以这样一种方式来认识它的,但它所谓的这个“名字”其实并不那么合适。我们来观察一本简简单单放在圆桌面上的书,书放在桌面上是静止的,对吗?这说明它的动量改变为0,而动量定理认为物体所受的合外力等于动量的改变值与时间之比。所以书所受到的合外力为0,只有两个大小相同、方向相反的力作用在这上:向下的地心引力与桌子向上的支持力。

因此,用这个单位m/s2地心引力的大小是多少?一般认为地心引力就等于书的质量与g的乘积。在地球表面,这样计算是成立的。但何谓g?假如你的回答是:g是重力引起的加速度的值,就会产生一个问题,书在这个时候并没有加速运动,对吧?
现在,如果你让书自由落体,那么作用在书上唯一的力就是地心引力。在这种情况下,它以9.8m/s2的加速度向下加速。但做自由落体运动只是物体发生的一种非常特殊的状态,这种情况并不能涵盖物体的其他状态,故不宜把g称为是重力引起的加速度,而应该称之为引力场的强度。
那么g的单位也应该随之变化吧?如果g是引力场强度,那么它的单位应该是单位质量上所受到力的大小,可以把它类比为电场里单位库伦所受的力的大小。把g称为重力场并不只是物理叫法上的正本清源,它还能帮助初学物理的学生理解“场”的概念,当有这个重力场的概念作为铺垫,以后学习到电场,理解起来就不会很费力。
言归正传,回到π的平方。也许你会认为π2的值和g相近只不过是世界上万千巧合里的一桩而已。然而,两者数值上的接近实际并非凑巧。但如果这件事不是巧合,那又为什么π的平方并不是完全和g相等?这是因为g本身也不是一个确值,它在地球表面的值是由很多因素决定的。首先,g是个近似值,是我们在地球表面测得的,由于受到地球自转的影响,它把参考系的加速度也考虑在内了,离赤道越近,g的值就越小。
另外一个影响g的因素来源于地球表面并不统一的地理条件。在一个由密度较大的岩石构成的区域,g的值会增加,其值随着地理区域的不同而发生变化,并没有一个统一的定值。
关于g,比前面还要有趣的来了:为什么两个看似毫不相关的π和g是有联系的?这个和长度单位“米”也有关系。具体阐述这个问题前,我们先来认识一下秒摆。秒摆是一种钟摆,重物从一头运动到另外一头耗时正好是1s(或周期为2s)。
你肯定见过秒摆,家里祖父的钟摆就是一个秒摆(周期为2s)。但从技术上来讲,祖父的钟摆并不是严格意义上的一个秒摆。秒摆一端用一根质量极轻的细线拴上一个质点(线可以在你家附近的五金店购买到)。而祖父的秒摆则完全不同,它有一根硬棒作为来回摆动的工具,棒有质心,它和秒摆的质心不一样。测量一下后者钟摆的长度,你会发现它的长度大致为1m。而真正意义上的一个秒摆的长度实际就是1m。当然如果你和你的朋友在地球上不同的区域各自制作一个秒摆,用到线长度可能稍有不同。
去试一下,找来一颗质量较小的物体比如坚果,或者一颗金属球。金属球的效果会非常好,因为它的重力远远大于空气的阻力以致于后者可以被忽略。现在,令金属球质心与支点的一端之间的距离为一米,并让它以小角度摆动(大约10°)。你可以用视频记录下来或者用秒表来测时间。不管怎么测,小球从一边摆到另一边,两种方式测得的时间都应为1s。
在此,我不加以推导直接给出小角度摆动的秒摆周期公式,但要从实验角度得出这个结果并不是特别困难:
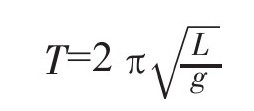
如果你希望周期达到2s,你可以通过公式自己调整线的长度。此时线的长度L正好可以由g和π2来表示。更近一步,如果长度如秒摆一样取1m,那么得出的结果g的值为π2,约等于9.8m/s2。等一下,刚才不是说g的单位N/kg吗?好了,现在通过运算你该明白了为什么说这两个单位是等价了吧?
但是为什么π会出现在单摆的周期公式里?这个问题问得好。这是因为单摆的路线和圆形一样吗?不对。在弹簧下端挂一重物,用手拉一下,重物就以原来静止的位置为中心上下做往复运动,这同样也是简谐振动,它的周期公式和小角度的单摆周期公式在形式上一样。那么到底为什么π在这个公式里?我认为最佳答案是描述简谐运动需要用到正弦与余弦函数,因为这个缘故,周期公式里才有了π。
很多表面看起来毫不相关的事物原来有着我们意想不到的联系。g和π就是这样一种情况,当然,有时候在其他没有圆的场合π依旧会出现。
