我的一位博客读者向我提出这样一个问题:
“一个奥林匹克场馆大小的泳池里注满了660000美制加仑的水。假设有一架秤位于整个泳池底部,称得的数据显示为5511556磅——水的重量。现用起重机一端吊住一颗质量为12000磅、宽5英尺的圆形钢球缓缓放入水中,球体的一半位于水面之上,一半浸没在水中,问这时秤的读数为多少?”

首先,让我来告诉你一个错误的答案:5511556磅。得出这个答案的思维过程并不复杂:如果起重机仍然支撑着球体的重量,那么球就不会施加任何重量给称。这是错误的。另一个错误的答案认为是6000磅。毕竟铁球一半露出水面,这一半并不是整体质量中的一部分。对吗?也不对。还有一个答案听上去似乎高明些:5511556磅,得出这个答案的依据是牛顿定律:如果球对水有向下的压力,那么这个力会被水的浮力抵消掉,所以秤的读数没有发生变化,是这样吗?这个答案有点接近了,但还是不正确。
当钢球一半置入水中时,对钢球做受力分析,以下为受力示意图:
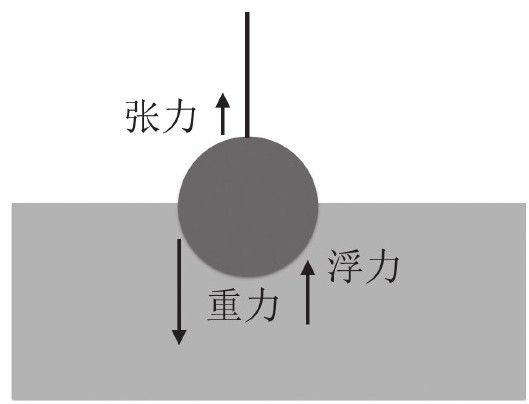
作用在球体上一共有3个力:
1.水的表面张力,它对球体作用力向上(一颗实心的钢球不会浮起来);
2.重力G重(mg,g为重力场强度);
3.浮力F浮,本质上,这是一个水对球向上的推力;
浮力的值如何计算?假设球的部分像这样由水替换掉:
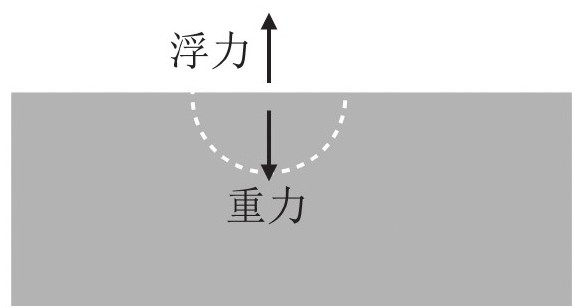
这张图显示,如果不是球让这部分水偏离原来的空间,水就会留在原处。对于这部分水而言,没有绳索拉扯的它受到一个向下的地心引力和一个向上的浮力。假设这部分水是静止的,那这两个力在大小上是相同的。
那么浮力是如何产生的?要想通浮力存在的原因,可以想像物体排开的那部分水有回到原空间的趋势因而对物体形成一个撞击力。进一步,这里有一个很酷的知识点:由于排开水而造成的撞击力是不因物体材质变化而变化的。只要物体体积相同,不论钢球还是其他材质,这种撞击力不变。这个想法妙在我会很清楚这部分水提供的浮力是多少。结合上面的叙述,浮力的大小等于这块被排开的水的重力。因为这一部分的水的体积和球体的体积完全一样,两者的浮力也是相同的。这样一来,浮力的大小自然就是水的密度、物体的体积和重力常数g的乘积。
上述这些和泳池底部的秤能建立什么关系呢?首先让我说明,我个人倾向于把牛顿第三定律称为“对于力的定义”。基本上,它表达了力是物体间相互作用的这样一种思考。如果说水以浮力F浮将球撑起,根据牛顿第三定律就可以反推,球对水也存在一个大小一样的向下压力,即为重力。
前面我讲的内容聚焦于对球体上力的分析,现在转向假设所有的水都放在一架秤上称重,在钢球放入水中之前,图式如下:
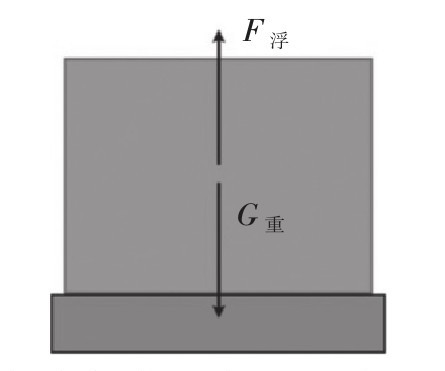
此时没有什么容器把水盛起来,水只是为了分析的简便起见简单“坐”在秤上。现把球放入水中,由于水以浮力向上推球,球就向下压水,其力的大小等于浮力,图式如下:
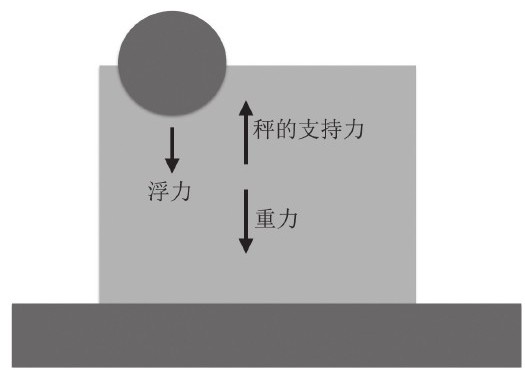
随着这个作用在水上,大小等于浮力的力,情况又发生了什么变化?水还是保持静止,这意味着合外力依旧是0(矢量为0)。既然增加了一个力,为什么合外力仍然为0?水的质量也没有变化,因为水并没有减少或者增加。唯一发生变化的是秤对于水的支持力。秤的支持力的增加就使得秤的读数必然也随之上升。上升了多少?上升的量就等于物体排开的那部分水的重量。
这里有两点是很耐人寻味的:首先,秤的读数变化和放置于水中的物体的材质无关,不管材料是钢还是轻木。物体排开的相等体积的水的重量就是秤读数的变化量。当然要轻木球沉得像钢球那样,必须施力向下摁住它。
另外一点是,从秤的读数角度而言,本质上到底是什么使得看起来似乎秤上的水增加了?我们知道,用秤的时候我们是不需要关注这些问题的。在正常情况下,称的使用是十分简单的,用的时候只要注意事先读数清零,要插上电,不用的时候锁好即可。但有时候你也需要关注此类表象性的问题。如果我把一颗体积为1m3的球放入水中,排开的水会导致整个泳池的水位上升1cm,从池底开始算,似乎水增加了(水位变深了),读数也增加了,而事实上水的总量没有变化。
很多人会觉得这样一个答案难以置信,为了帮助他们理解,我做了一个小实验。我把烧杯中注上适量的水后放在秤上,烧杯的重量加上水的重量一共是254g,我把一个球一半没入水中,下一步为了测量到保持这个球的位置所需要的拉力,我改用弹簧秤来拉球。
实验结果:随着一半球放入水中,大秤的读数从254g增加到了268g;在弹簧秤上球的质量从没入水之前的206g变化为192g。弹簧秤上读数的减少正好是大秤读数的增加。假如把这个球用同等体积的木球替换情况由会如何?依上述原理,秤的读数变化还会是那么多。
二次试验结果:大秤读数果然上升了约14g(实际是13g)。现在你明白了其中的道理了吗?当然这个问题你也可以动手自行解答,找到一台秤和一瓶水并不困难,只要把球放进水中,记录好称的读数就可以验证了。
这个问题不失为一个好问题,而我们的回答则更为出彩。
