老式计算机的工作原理

随着科技的进步，计算机技术得到了飞速发展，现在来探讨一下老式计算机是如何工作的，然后用老式计算机来求解方程。在前面的章节中我们知道，计算机能完成很多任务，比如下象棋，计算机还可以完成一些其他的任务，比如进行语言的翻译，甚至演奏出美妙的乐曲等。只要事先编写好程序，计算机就会按照这些程序来工作。

在此我们不打算去研究那些下象棋或者翻译的程序，因为它们相当复杂。我们只介绍两个比较简单的程序，看看计算机是如何工作的。

在此之前，先来看一下计算机的构造。

我们已经知道，计算机可以在1秒内完成上万次的运算。在计算机中，完成这一功能的装置称为运算器。另外，计算机还包括控制器和记忆装置——存储器，常用存储器来存放数据或者信号。当然，计算机还包括一些用来输入、输出的装置。通常来说，这些结果都通过打印机打印到卡片或者纸张上。

我们可以把声音记录在唱片或者胶卷上，以便以后重新播放。但是，如果在唱片上录音，通常只能录一次，唱片不能反复录音。有时候，我们还会把声音记录在磁带上。磁带有一个好处，可以擦掉重新录。在同一根磁带上可以重复录音，只需要把以前的录音擦掉就可以了。

计算机的记忆装置就是根据以上的原理进行工作的。数据以及电、磁、机械等信号，被写在专用的硒鼓、磁带或者别的记忆装置上。当需要这些数据或者信号的时候，就把它们“读”出来。当不需要以前的数据和信号时，就可以把它们擦掉，再写上新的数据和信号。对于计算机来说，完成这些操作只需要不到0.1秒。

存储器由几千个单元组成，而每个单元又包含几十个用来存储的元件，比如磁性元件。计算机存储的都是二进制数，我们规定数字“1”用磁化了的元件表示，数字“0”用没有磁化的元件表示。比如，一个存储单元（表示一个二进制数）由25个元件组成，通常用第一个元件表示这个数的符号，即正或负，接下来的14个元件用来存储这个数的整数部分，后面的10个元件用来存储小数部分。如图所示，这是一个简单的存储器，它由两个单元组成，每个单元有25个元件。“+”号表示磁化了的元件，“－”号表示没有磁化的元件，此外，一般用逗号表示小数点。在图中上边的单元中，用虚线把表示符号的第一位和其他位分开，我们可以读出这个二进制数为+1011.01，如果换算成十进制数，就是11.25。

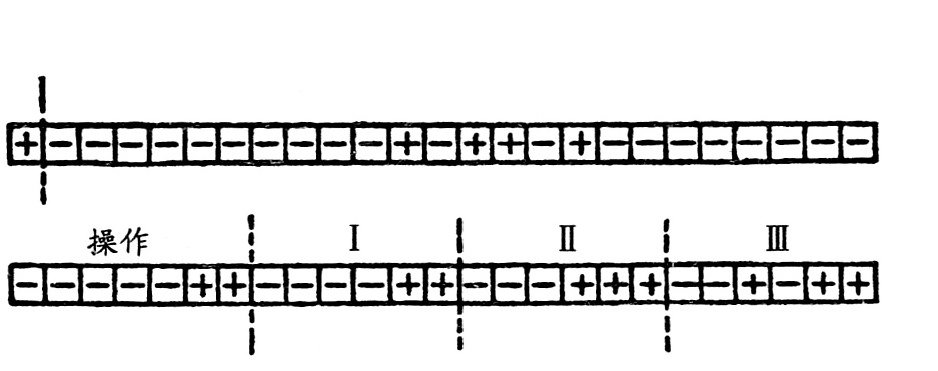
在存储单元中，除了数据，还可以写入指令，程序就是由这些指令组成的。下面，我们就来看一下通常所说的三地址计算机的指令。为了写入指令，通常把存储单元分成4部分，如图中下面的单元所示，每段用虚线隔开。第一部分表示操作，它是以数的形式写在存储单元里的。例如：

加——操作Ⅰ，

减——操作Ⅱ，

乘——操作Ⅲ，

……

可以这么理解指令：存储单元中的第一部分为操作码；第二部分和第三部分为编号，或者说地址码，要想进行操作，就需要从这两部分中取出需要的数；第四部分是用来存放运算结果的地址码。例如，在图的下行中写进的二进制数是11，11，111，1011，换算成十进制数就是3，3，7，11，它们的意思是：对3号和7号存储单元中的数执行操作Ⅲ，也就是进行乘法运算，最后得出的结果写入11号存储单元中。

如果不用二进制数，而是直接用十进制数，那么要执行上面的指令，就可以写成下面的形式：

乘3 7 11

下面，我们来看两个非常简单的程序。

程序1：

（1）加 4 5 4

（2）乘 4 4 →

（3）转移 1

（4）0

（5）1

那么，计算机是如何工作的呢？从这里可以看出，在计算机的前5个存储单元中，存放着上面的数据和指令。

第1条指令：把存放在4号和5号存储单元中的数进行加法运算，然后把计算结果送回到4号单元中，覆盖掉原来的数据。也就是说，把0+1的结果“1”写入4号存储单元。这样，第一条指令就完成了，这时候，4号和5号存储单元里的数据就变为：

（4） 1

（5） 1

第2条指令：把存放在4号单元中的数据“1”跟自己相乘，也就是进行平方运算，然后把结果1输出到卡片上（这里的箭头“→”表示输出）。

第3条指令：转移到1号单元。这里用到了一个转移指令，它的意思是，返回第1条指令，重复执行每一条指令。

第1条指令：把存放在4号和5号存储单元中的数进行加法运算，把结果送回到4号单元中。现在4号单元中的数据变成了2，即

（4） 2

（5） 1

第2条指令：把存放在4号单元中的数据“2”跟自己相乘，把结果4输出到卡片上。

第3条指令：转移到1号单元，重复执行第1条指令。

第1条指令：把数据“3”送到4号单元中，即

（4） 3

（5） 1

第2条指令：把3²=9输出到卡片上。

第3条指令：转移到1号单元。

……

从以上的分析可以看出，机器依次对整数进行平方运算，并把结果输出到卡片上。我们不需要自己动手来写计算出的数据，机器会自动取出所有的整数，并把它们进行平方运算。通过这个程序，机器可以在很短的时间内完成1到10000的平方运算。

需要指出的是，这里我们把程序进行了简化，实际程序比刚才列出来的要复杂得多。特别是在第2条指令中，机器把结果输出到卡片上需要的时间比计算一次所用的时间多得多。所以，通常先把结果寄存到一些空的存储单元中，然后再慢慢地输出到卡片上。在上面的例子中，第一次运算出的结果寄存到1号空单元中，第二次的结果寄存到2号空单元中，第三次的结果寄存到3号空单元中，等等。在前面的程序1中，我们并没有把这一点考虑进去。

除此之外，由于存储单元是有限的，所以机器不可能无休止地进行这种平方运算。在上面的程序中，我们无法确定机器是否已经完成了我们需要的数据，所以，这就需要在程序中增加一条指令，使机器在需要的时候能够及时停止程序的运行。比如，我们希望机器完成从1到10000的平方运算后自动停止。

当然，很多指令要复杂得多，这里就不介绍了。

下面的程序就是用来对1到10000中所有整数进行平方运算：程序1（a）：

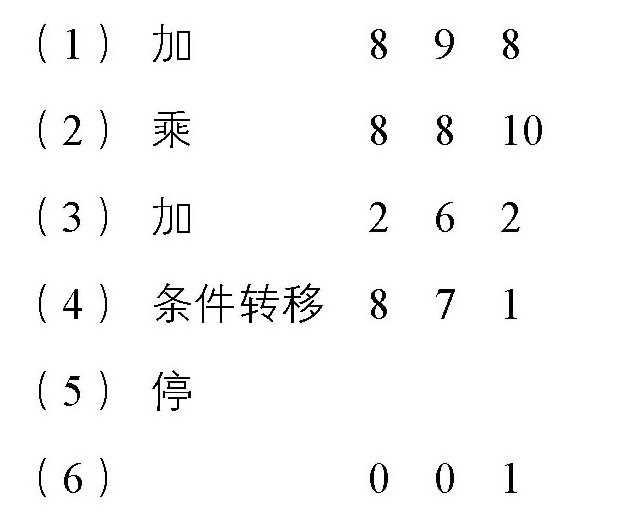
（7）10000

（8）0

（9）1

（10）0

（11）0

（12）0

第1条和第2条指令跟前面的程序1一样，执行完这两条指令后，8，9，10号单元中的数据将是：

（8）1

（9）1

（10）1²

也就是说，执行完第3条指令后，第2条指令中有一个地址变了。在后面我们会说明这么做的原因。

第4条指令：这里的“条件转移”就相当于前面程序1中的第3条指

令，该指令是这样操作的：如果8号单元中的数据比7号单元中的数据小，就返回到第1条指令；否则，就执行下面的第5条指令。由于现在的情形是1＜10000，所以，继续执行第1条指令。执行完第1条指令后，8号单元中的数据变为2。

现在第2条指令中的内容为：

它的意思是：把2²送到11号单元中。现在我们可以看出为什么有第3条指令了，因为10号单元被占用了，所以新产生的数据2²不能再送到10号单元，而是送到下一个单元中。执行完第1条和第2条指令后，8至11号单元中的数据变为：

（8）2

（9）1

（10）1²

（11）2²

执行完第3条指令后，2号单元中的指令变为：

这时候，8号单元中的数据仍然比7号单元中的“10000”小，所以，继续执行第1条指令。

执行完第1条和第2条指令后，8号至12号单元中的数据变成：

（8）3

（9）1

（10）1²

（11）2²

（12）3²

……

只要8号单元中的数据比7号单元中的“10000”小，程序就会一直执行下去，只有当8号单元中的数据变成“10000”时，也就是把从1到10000中所有的整数进行了平方运算，程序才会停止执行。这时，由于8号单元中的数据不再小于7号单元中的“10000”，所以，第4条指令不再转移到1号单元，机器会往下执行第5条指令：停止。

下面来研究一个复杂些的程序：解方程组。为简单起见，这里只列出一个简化的程序，如果读者朋友对此感兴趣，可以自己写出这个程序。

假设有一个方程组：

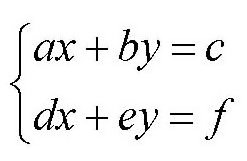
这个方程组并不难求解，容易得出：

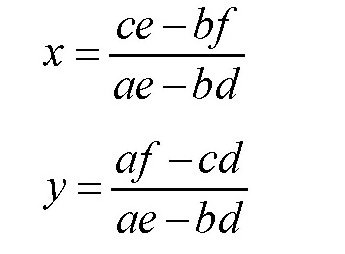
一般情况下，手动求解这个方程组至少需要几十秒的时间。但如果交给计算机，它可以在1秒的时间里完成几百个这类方程组的求解。

下面，我们就来看一下求解方程组的程序。假设有很多个方程组，如图所示，方程组中的a,b,c,d,e,f,a,b,c′′′LL都是已知数。程序如下：

程序2：

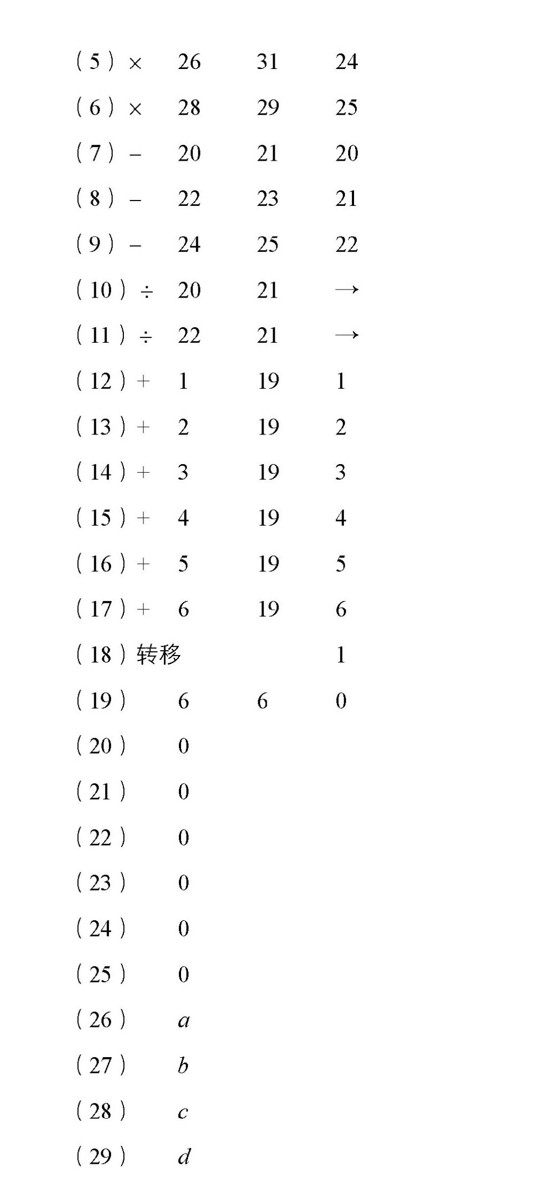
（30）?????e

（31）?????f

（32）?????a′

（33）?????b′

（34）?????c′

（35）?????d′

（36）?????e′

（37）?????f′

（38）?????a′′

……

第1条指令：把28号和30号单元中的数据进行乘法运算，把得到的乘积送入20号单元。也就是说，把数据ce写入20号单元。

然后，按顺序执行第2条到第6条指令。执行完这5条指令后，20号到25号单元中的数据变成：

（20）ce

（21）bf

（22）ae

（23）bd

（24）af

（25）cd

第7条指令：用20号单元中的数据减去21号单元中的数据，然后把结果（ce-bf）送到20号单元中。

依次执行第8条和第9条指令。于是，20号至22号单元中的数据变成：

（20）ce－bf

（21）ae－bd

（22）af－cd

第10条和第11条指令：进行除法运算

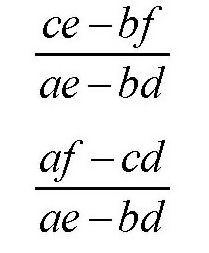
并把结果输出到卡片上，这就是上面方程组的解。

这样，就解出了第一个方程。读者可能会问，既然已经解出了方程，那后面的指令是干什么用的？其实，后面的指令是用来求解后面的方程组的。我们不妨再来看看这个过程是如何进行的。

第12条到第17条指令的意思是，把1号到6号存储单元中的数与19号单元中的数进行加法运算，并把结果送到1号至6号单元中。执行完这些指令后，1号到6号单元变为：

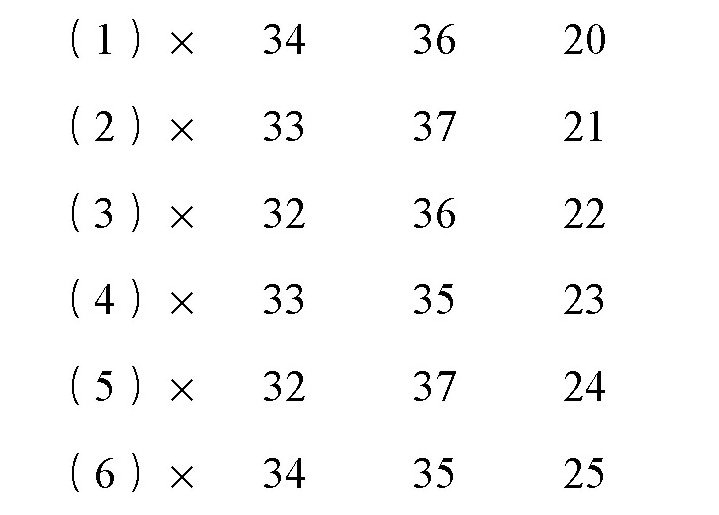
第18条指令：转移至1号单元。

可以看出，1号到6号单元中的内容变化了，那它们跟原来的内容区别在哪儿呢？在这些单元中，原来的地址编号为26至31，现在变成了32至37。也就是说，机器会重复刚才的运算，但是，这次不再从26号至31号单元中提取数据，而是从32号至37号单元中提取，这里存放着第二个方程组的系数。这样，机器就会把第二个方程组解出来。同样的道理，可以解出第三个、第四个……依此类推。

从以上的讨论可以看出，程序编写得是否正确，对于解决问题非常重要。机器本身一无所知，它仅仅是按照程序来执行。除了上面求解方程组的程序，还有开方的程序、求对数的程序、求正弦的程序、求解高次方程的程序等。前面的章节中，我们还提到了下象棋的程序、翻译的程序等。很多程序都可以用机器解决，问题越难，程序也越复杂。

我们还要说明一点，有一种程序，可以用它来编写程序。借助这个程序，机器可以自动编写出一些解题程序来，这样就大大减轻了人们的负担，要知道，编写程序是一项很繁重的工作。