在一次小学数学课上,老师在黑板上用粉笔标出了两个点,并对一位学生说:“请你在这两个点之间画出最短的路线。”说着,他把粉笔给了学生。只见学生拿过粉笔,想了一会儿后,用一条曲线把那两个点连了起来。
老师感到很生气,便说道:“我们说过,在两点之间,直线是最短的!你刚才为什么画了一条曲线呢?”
“我爸爸教我的,”那个学生答道,“他是开公共汽车的,每天都开呢!”
你是否也跟这位老师的想法一样?如图所示,很多读者朋友都知道,图中的曲线正好是南非的好望角跟澳大利亚最南端之间的最短路线,所以,我们没有理由嘲笑那位学生。实际上,我们还可以看到更加不可思议的事情。图中表示的是从日本横滨到巴拿马运河的两条路线。相比而言,那条半圆形的路线要比直线短多了。
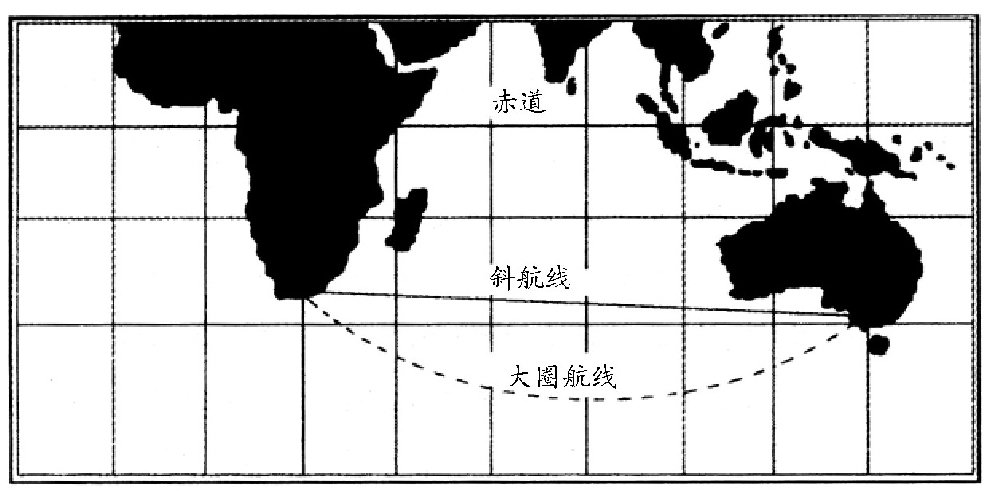
图在航海图上,南非的好望角与澳大利亚南端之间的最短路线竟然是曲线(大圈航线),而不是直线(斜航线)。
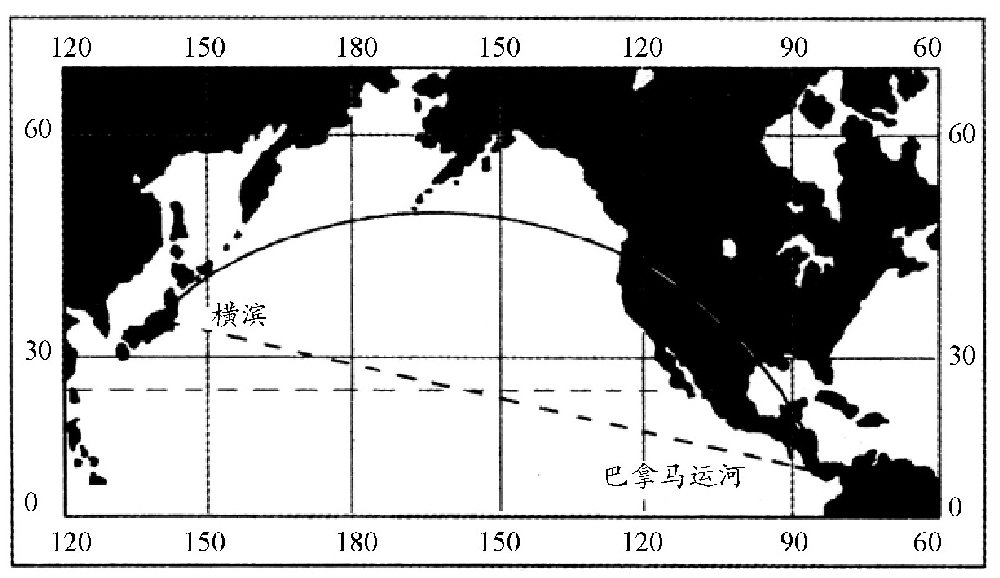
图在航海图上,连接日本横滨与巴拿马运河的曲线航线,竟然要比这两点之间的直线航线要短。
你可能觉得我在开玩笑。其实不然。前面提到的这些都通过地图测绘员的测绘得到了证实。
那么,该如何解释这个问题呢?这时,我们不得不提到地图,特别是航海图。我们先看一下地图的基本知识。地球是球体,从严格意义上说,它的任何一部分都不可能完全展开成一个中间不重叠、不破裂的平面。所以,要想在一张纸上真实地画出某块陆地是不可能的事情。人们在绘制地图时,也就不可避免地会进行一些歪曲,从某种意义上说,要想找到一张没有任何歪曲的地图是不可能的。
下面,我们再来说一下航海家经常用到的航海图,提到它,就不得不提一下16世纪的荷兰地理学家墨卡托,正是他发明了绘制方法。我们通常把这种方法称为“墨卡托投影法”,如图所示。这种地图带有格子,人们很容易看懂,上面的所有经线都是用平行的直线来表示,所有的纬线都是用与经线垂直的直线来表示。
那么,我们提出这样一个问题:如何在同一纬度上找出两个海港间最短的航线呢?你可能会说:只要知道最短航线的位置以及它所在的方向就行。那么,接下来你可能就会很自然地想到,最短航线一定在两个海港所处的纬线上,因为地图上的纬线都是用直线来表示的,所以我们可以用“两点之间直线最短”的原理来解答。但是,很遗憾地告诉你,答错了,你刚才找出的这条航线并不是最短的。
下面,我们就来分析一下。在一个球面上,两点之间的最短路线并不是它们的直线连线,而是经过这两个点的一条大圆(在球面上,圆心与球心重合的圆称为大圆)弧线。这条大圆弧线的曲率小于这两个点之间任何一条小圆弧线的曲率,并且,球的半径越大,大圆弧线的曲率就越小。所以,看似直线的纬线,实际上都是一个个小圆。也就是说,最短的路线并不是在纬线上。我们可以通过实验证明。拿一个地球仪,在上面任选两点,用一条细线沿着地球仪的表面把这两点连起来,然后,拉紧这条细线,你会发现,这条细线与纬线根本不在同一条直线上,如图所示。从图中可以看出,在这两点之间,拉紧的细线才是最短的航线,与地球上的纬线根本不重合。也就是说,在航海图上,两点之间的最短距离并不是一条直线。这是因为纬线都是曲线,而在地图上我们通常用直线来表示。反之,在地图上,任何一条与直线不重合的线都是曲线。

图通过图示的实验可以证明,最短的航线并不在纬线上。
由此可知,在航海图上,为什么最短航线是曲线而不是直线了。
再说一个例子,很多年以前,俄国出现过一场较大的争议。当时人们想在圣彼得堡和莫斯科之间修一条铁路(即十月铁路,又叫尼古拉铁路),但关于这条铁路是直线还是曲线的问题引起了争论。最后,还是沙皇尼古拉一世出面,作出了这样的结论:这条铁路是一条直线而不是曲线。我们可以想一下,如果当时尼古拉一世使用了图所示的地图,他可能就不会得出上面的结论了,他会发现:这条铁路是一条曲线,而不是直线。
此外,我们还可以通过下面的方法进行计算,可以进行更严格的论证。
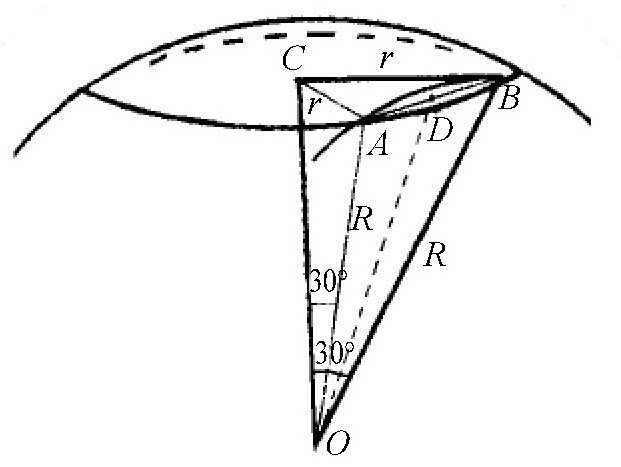
图比较一下图中所示地球上A、B两点之间纬圈弧线和大圆弧线,哪一条更长?
在地图上,曲线航线比直线航线要短。我们不妨假设存在这样的两个港口,它们之间的距离是60°,而且,它们都跟圣彼得堡一样,在北纬60°上。至于这两个港口是否真的存在,我们这里不作讨论。如图所示,地心为点O,A、B分别表示这两个港口,弧线AB位于纬线圈上,它的弧长是60°,点C为AB所在的纬线圈的圆心。我们以地心O为圆心,经过点A和B画一条大圆弧线,显然,半径OB=OA=R;可以看出,这条大圆弧线跟纬线圈上的弧线非常接近,但它们并不重合。我们还可以计算出每条弧线的长度。根据题意,点A和点B都处于北纬60°上,所以,半径OA和OB跟地轴OC的夹角都是30°。但是,我们知道,在直角三角形ACO中,30°夹角所对应的边AC(它等于纬线圈的半径),应该等于直角三角形的弦AO的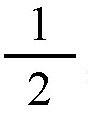
也就是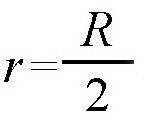
而纬线圈上的弧线AB(60°)的长度为纬线圈总长度(360°)的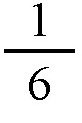
由于纬线圈的半径r为大圆半径R的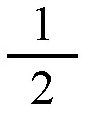
所以纬线圈的长度也是大圆长度的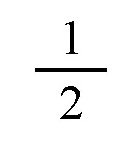
大圆的长度是40000千米,所以,纬线圈上的弧线AB的长度就是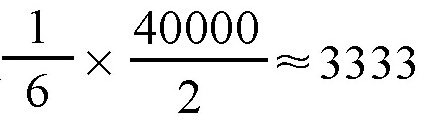
千米。
另外,我们还可以计算出经过点A和点B的大圆弧线长度,也就是这两个港口之间的最短路线。这时,我们需要先计算出∠AOB的大小。小圆上60°弧所对应的弦AB正好。是它的内接正六角形的一条边,所以,我们有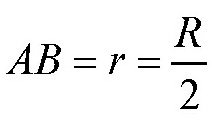
连接点O与弦AB的中点D,得到直线OD,这样便有了一个直角三角形ODA,其中,∠D为90°,又:
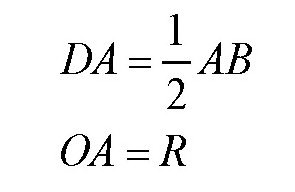
所以有:
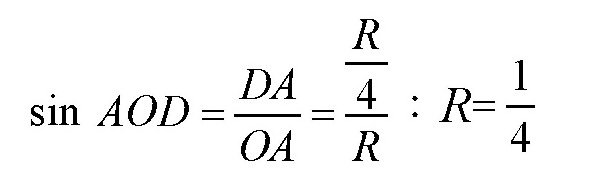
由三角函数表得:
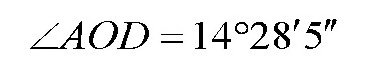
所以:
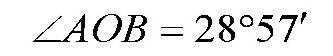
计算出这些数据后,我们就很容易得出最短路线的长度了。对地球来说,大圆1分的长度大约等于1海里,即1.85千米,于是有: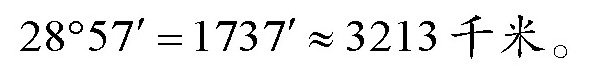
综上所述,在航海图上,沿纬线圈的直线航线是3333千米,而大圆上的航线(地图上是曲线)是3213千米,也就是说,后者比前者少了差不多120千米。
如果你想检验一下图中所画的曲线是不是大圆弧线,方法也很简单,只用一个地球仪和一条细线就可以了。在图中,在非洲好望角和澳大利亚之间,它们的直线航线为6020海里,但曲线航线仅有5450海里,二者相差了570海里,即1050千米。从地图上,我们可以很容易看到,在上海和伦敦之间,如果画一条直线航空线,一定会穿过里海,但是,它们之间的最短航线却是经过圣彼得堡再往北这一条。通过分析可以看出,在航行中,如果不事先弄清航线问题,可能会浪费很多燃料和时间。
在当代,节省燃料和时间具有非常重要的意义。现在毕竟不是那个依靠帆船航海的时代了,时间对于我们每个人来说都是非常宝贵的。轮船出现后,时间就变成了金钱,航线缩短,就意味着使用的燃料减少,自然所需要的费用也就少了。所以,航海家们现在使用的不是墨卡托地图,而是一种叫作“心射”的投影地图,这种航海图用直线来表示大圆弧线,通过它,可以保证轮船始终沿着最短的航线前进。
那么,对于以前的航海家们来说,他们是否知道前面所说的知识呢?答案是肯定的,那他们为什么在航海的时候还是使用墨卡托地图却不走最短的航线呢?其实,这就如同硬币有两面一样,虽然墨卡托地图有这样那样的缺陷,但在一些特定的条件下,它却可以给航海家们带来很大的帮助。
(1)除了距离赤道很远的地方,墨卡托地图所表示的小块陆地区域的轮廓大体是准确的。在那些距离赤道越远的地方,地图上表示出来的陆地轮廓比实际要大,并且,纬度越高,陆地轮廓被拉伸得越厉害。对于外行人来说,可能不理解这种航海图。例如,在墨卡托地图上,格陵兰岛的大小看起来跟非洲大陆差不多,而阿拉斯加看上去比澳大利亚大多了。但实际上,格陵兰岛的面积只有非洲的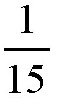
而阿拉斯加和格陵兰岛的面积相加,也只有澳大利亚面积的一半。不过,对于那些熟知墨卡托地图特点的航海家们来说,这种地图上表示出来的大小并不是问题,他们能对这些小缺陷持包容态度,因为在很小的区域内,航海图上所表示的陆地轮廓跟实际上相差不大,如图所示。
(2)在航海中,使用墨卡托地图可以带来很大的方便,因为它是唯一用直线表示轮船定向航行航线的一种地图。“定向航行”指的是轮船航行的方向、方向角保持不变。也就是说,在航行时,轮船的航线跟所有经线相交的角度始终相等。这些航线又被称为“斜航线”(缠绕在地球上的螺旋状曲线才是斜航线),只有在这种用平行直线表示经线的地图上,才可以用直线表示航线。我们知道,地球上的所有纬线圈与经线圈都垂直,即它们的夹角为直角,所以,在墨卡托地图上,经线都垂直于纬线。简单来说,看上去全是经纬线绘成的方格网,这也正是墨卡托地图的特点。
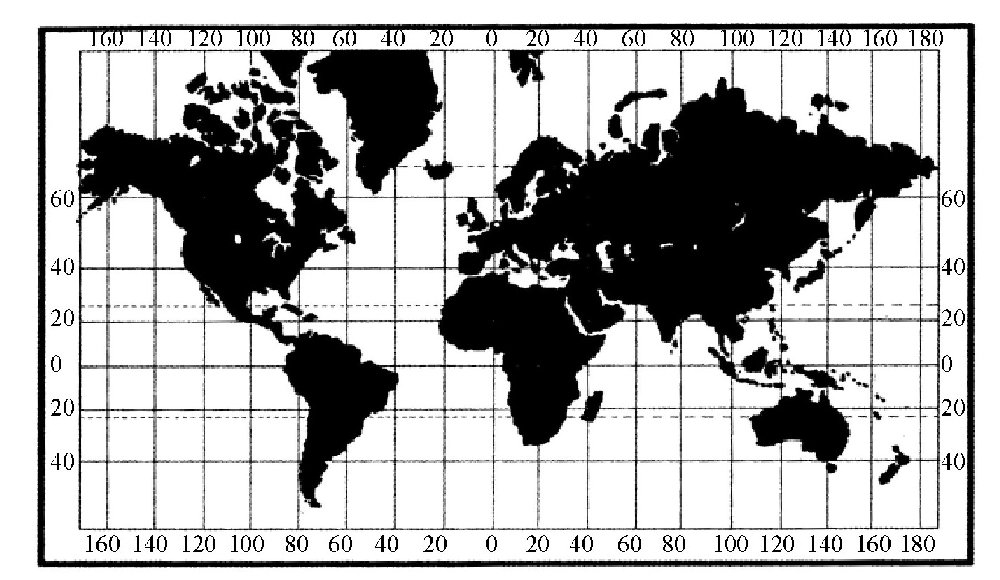
图全球航海图,又叫墨卡托地图。在这种地图上,高纬度地区陆地轮廓被拉伸了,比如,格陵兰岛比非洲的面积还要大。
由此可以看出,航海家们非常喜欢使用墨卡托地图是有原因的。如果一名船长想要到某个海港去,他可以这么做:首先用尺子在出发地和目的地之间简单画一条直线,然后,测量出这条直线跟经线的夹角,由此确定出航行的方向。在浩瀚无垠的大海上,船长只需要保证轮船始终朝着这个方向前进,就一定可以准确到达他想要去的那个海港。从这里可以看出,这条斜航线虽然不是最短、最经济的,但对于船长和船员们来说,却是最方便的。再举个例子,如果我们想从南非的好望角出发,去澳大利亚的最南端,如图所示,那么,我们只需要保证轮船一直朝着南偏东87°50′的方向前进就行了。但是,如果我们想沿着最短的航线走,就必须不停地改变航行的方向,首先沿着南偏东42°50′的方向,在到达了某个地方后,再改为偏东39°50′的方向。实际上,这条最短航线根本不存在,如果这么航行,到达的就是南极了。
有意思的是,斜航线和大圆航线在某些地方可能会重合,当我们沿着赤道或者经线航行时就是这样。这是因为,在墨卡托航海图上,这些地方的大圆航线也正好是用直线表示的。不过,除此之外,其他任何地方的斜航线与大圆航线都不一样。
