在俄国,有一位英雄叫克雷莫夫。他跟朋友们曾经进行过一次飞行实践,路线是从莫斯科开始,飞到北极上空,然后又飞到圣大新多。最终,他以62小时17分钟的飞行时间打破了两项世界纪录:在不着陆的情况下,实现了10200千米的直线飞行和11500千米的折线飞行。
假设有一架飞机,沿着子午线,从东半球北纬某一纬度上的某个点飞越北极,在48小时后,它到达了西半球北纬同一纬度上的一点。那么,这架飞越北极的飞机,是否也会跟地球一样绕地轴旋转呢?
我们经常听见这个问题,但是,得到的答案却并不一致。不管是什么飞机,只要飞过北极,肯定会跟着地球一起旋转。这是因为,飞机在飞行时,并没有飞越大气层,只是离开了地球的硬壳表面,它仍然被地球带着,围绕着地轴在旋转。
所以我们说,这架飞机在飞越北极时,会随着地球围绕地轴旋转。但是,新的问题又来了,飞机飞行的轨迹是什么样子的?

怎样回答这个问题呢?有一点需要注意,如果我们说“一个物体在运动”,通常是指这个物体相对于另外一个物体发生了位置的改变。所以,物体的轨迹终究还是运动的问题。如果提出这个问题的时候,并没有指明坐标系,或者,通俗一点儿说,并没有告诉我们相对于什么物体发生了运动,这个问题就会变得没有任何意义。
如果一架飞机沿着子午线飞行,那么它一定也跟着地轴在旋转。这是因为,子午线跟地球在一起,也会围绕地轴旋转。但是,对于地球上的观察者来说,并不能感受到这个飞行的真正轨迹,因为它围绕地轴旋转这一点是相对别的物体而言的,并不是指地球。
所以,对于地球上的我们来说,这架飞机飞越了北极,并形成了轨迹。如果飞机是准确沿着子午线飞行的,并且一直跟地球的中心保持相同的距离,那么,这个轨迹就是一个大圆上的一段弧线。
现在,我们的问题是:我们已经得到了飞机相对于地球的运动轨迹,而且还知道,这架飞机会跟着地球一起围绕地轴旋转。也就是说,我们知道,地球和飞机都在相对于第三个物体进行运动,那么,如果观察者是站在第三个物体上,飞机的飞行轨迹会是什么样子的?
这个题目看起来有些复杂,我们不妨把它简化一下。假设地球的北极周边是平的圆盘,它所在的平面跟地轴垂直。假设这个圆盘在这个平面上围绕地轴旋转。我们再假设有一辆玩具车,它沿着圆盘的直径向前匀速移动,用它来表示飞机沿着子午线飞越北极。
【题目】这辆玩具车在这个平面上走的路径是什么样的?确切的说,是玩具车上的某个点,比如说它的重心,它的移动轨迹是什么样子的?
其实,这辆玩具车从直径的一端运动到另一端所花的时间,取决于它的运动速度。
下面,我们分三种情形进行分析:
●玩具车花12个小时跑完全程。
●玩具车花24个小时跑完全程。
●玩具车花48个小时跑完全程。
我们知道,那个圆盘围绕地轴旋转一圈花的时间是24个小时。
第一种情况:如图所示,如果玩具车花12个小时跑完了圆盘的直径长度。在这个时间里,圆盘转了半圈,转了180°。也就是说,点A和点A′正好互换了一下位置。在图中,圆盘的直径被分成了8个相等的部分,玩具车跑完每一部分花的时间是12÷8=1.5个小时。那么请问,玩具车走了1.5个小时之后,它走到了什么地方?如果圆盘不旋转,玩具车从点A出发,走了1.5个小时之后,会到达点b。但是,圆盘并非不动,它是旋转着的,在这1.5个小时中,它旋转的角度是180°÷8=22.5°。所以,玩具车到达的位置就不是点b了,而是点b′。这时,对于观察者来说,如果他也是坐在这个圆盘上,那么他就感受不到圆盘的旋转,只看到汽车从点A到达了点b。但是,如果观察者在这个圆盘的外面,并没有随着圆盘旋转,那么他看到的就是另一种情形。对于他来说,玩具车到达了点b′。再经过1.5个小时的话,在圆盘外面的观察者看到玩具车走到了点C′。在下一个1.5个小时里,观察者会看到玩具车是沿着弧线c′d′运动的,再过1.5个小时,汽车会到达圆心e。
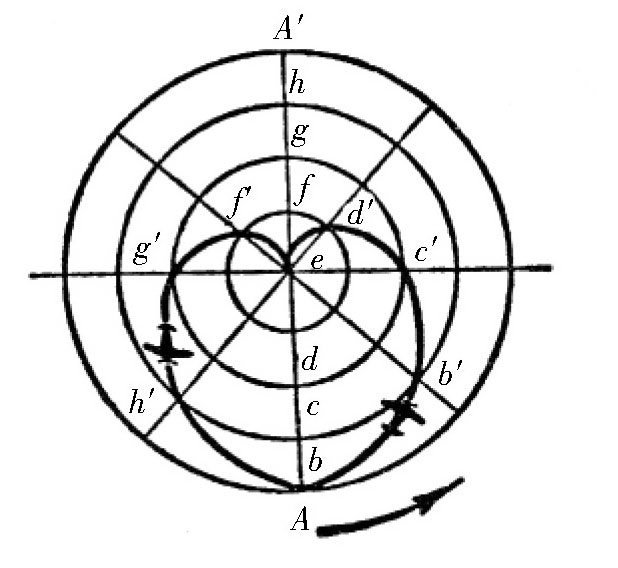
图 第一种情况。
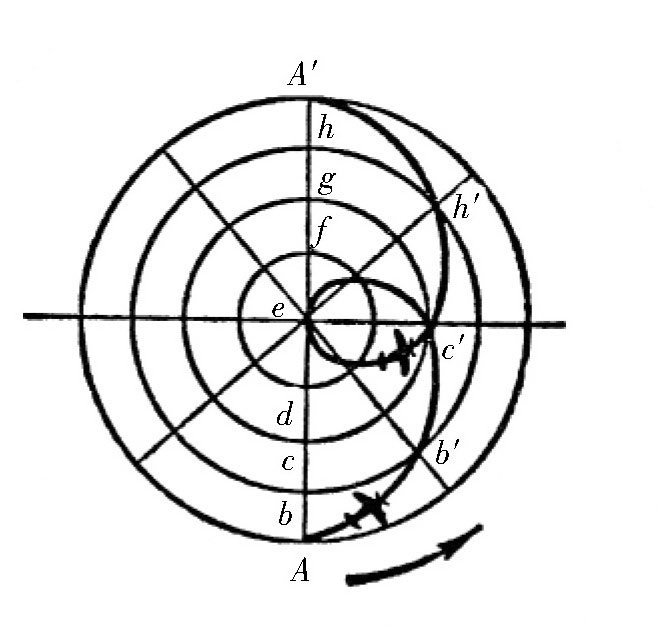
图 第二种情况。
对于站在圆盘外面的观察者来说,如果继续观察玩具车的运动轨迹,他看到的是非常意外的情形:玩具车画出了一条曲线ef′g′h′A。更奇怪的是,玩具车最终停在了出发点A上,而不是到了直径的另一端A′。
其实,这个意外的结果并不难解释。玩具车沿着直径的后半段走了6个小时,在这段时间里,玩具车行驶半径跟着圆盘转了180°,也就是说,它占据了直径的前半段所在的位置。更有甚者,汽车在通过圆盘的中心时,仍然跟着圆盘旋转。只不过,在圆盘的中心点上,不可能放下整辆汽车。其实,汽车上只有一个点跟圆盘的中心点正好吻合,这一时刻发生在一瞬间。接着,整辆汽车继续跟着圆盘围绕这点旋转下去。对于前面提到的飞机,在它飞越北极的时候也是一样的。所以,沿着圆盘的直径,玩具车从一端到了另一端,在不同的观察者看来,形状是不同的。对于站在圆盘上的观察者来说,这个路径是一条直线,而对于在圆盘外面没有跟圆盘一起转动的观察者来说,这个路径是一条如图所示的曲线。
如果具备下述条件,我们也可以看到这条曲线:假设飞机飞越北极的时间是12个小时,那么,如果从地球的圆心来观察飞机,把它的运动看成跟地轴垂直的平面运动,就可以看出来了。这里我们假设地球是透明的,你和那个平面都不跟着地球旋转。
这里,我们讲了两个有关运动的有趣例子。实际上,飞机飞越北极到另一半球所花的时间并不是12个小时。下面,我们再来看一个类似的问题。
第二种情况:如图所示,玩具车跑完直径长度花的时间是24个小时。在这24个小时中,圆盘正好自转了一圈,所以对于没有跟着圆盘转动的观察者来说,玩具车的运行路径形状如图所示。
第三种情况:如图所示,圆盘旋转一圈所花的时间仍然是24个小时,但是,玩具车跑完直径的长度所花的时间是48个小时。在这种情况下,如果汽车跑了直径的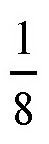
长度,它所花的时间是48÷8=6个小时。
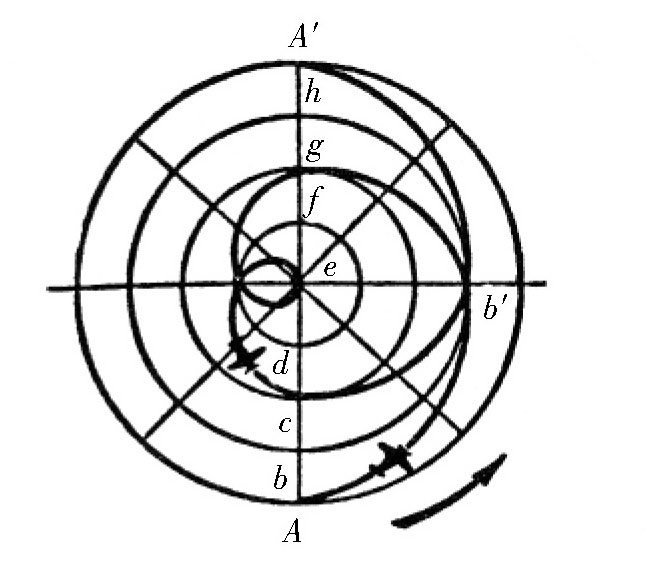
图 第三种情况。
那么,在这6个小时中,圆盘转动的角度将是一圈的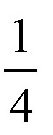
,也就是90°。所以,玩具车跑了6个小时后,如果圆盘没有转动,它应该沿着直径跑到点b处。但是圆盘是一直转动的,所以,它跑到了点b′。下一个6个小时候,它跑到了点g……48个小时之后,玩具车会跑完直径全长,圆盘整整转了两圈。所以,这两个运动会叠加。在圆盘之外的观察者看来,它的运行轨迹将是图黑线所示的一条连续曲线。
本节一开始提到的关于花了48个小时飞越北极的飞机的情形,跟这里的第三种情况是一样的,从俄罗斯的莫斯科飞到北极要花24个小时。如果我们是从地球的圆心来观察这个飞机,那么就会看到,它的飞行轨迹如图中的直线路线,接下来的飞行所走过的路线长度。大概是前面的1.5倍。此外,从北极到圣大新多的距离正好是从莫斯科到北极距离的1.5倍。所以说,在位置不变的观察者看来,整个飞行的后半部分和前半部分一样,轨迹也是直线的,只不过这个距离是前者的1.5倍。
最终,飞行轨迹所形成的曲线如图所示。对于既没有参加飞行,也没有跟着地球旋转的观察者来说,这就是从莫斯科到圣大新多的飞行路线。也就是说,如果我们站在地球的圆心来观察这架飞机的飞行轨迹,会看到飞机飞越北极形成的轨迹就是这个样子。
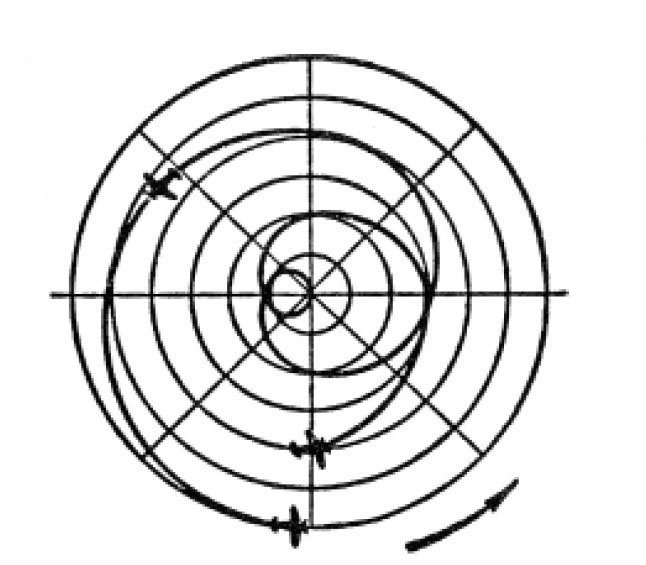
图 飞机的飞行轨迹。
那么,是不是说这条复杂的路线就是这架飞机飞越北极的真正轨迹呢?其实不是的,这条路线只是没有跟着地球旋转的人眼中的样子,就像一般的飞行也是相对旋转着的地球来说一样。
如果我们可以在月球或者太阳上观察这个飞行,那么,我们看到的飞行轨迹的形状将会更加奇怪。
我们知道,月球并没有随着地球的自转而转动,但是它每个月都要围绕地球旋转一圈。如果飞机飞越北极花了48个小时,月球围绕地球走过的弧线大概是25°。如果从月球上观察这架飞机,也会影响到飞行轨迹的形状。另外,如果在太阳上观察这架飞机的飞行,还需要考虑第三种运动对它的影响,也就是地球会围绕太阳转动。
在恩格斯所著的《自然辩证法》中,有这样一段话:“不存在单个物体的运动,所有的运动都是相对的。”通过本节的学习,读者朋友们肯定会对此有深刻的认识。
