让聪明的台球来倒水

在前文中，我们通过简单的几何作图方法，解决了一个打台球的题目。现在，我们让台球自己解答一个很有意思的古老的问题。

这怎么可能呢！台球还会思考？这是真的。如果我们要进行某种计算，并且已经知道了题目中给出的已知条件、接下来的计算方法，以及计算顺序，那么我们是可以把这项工作交给机器来完成的，它会比我们计算得还要快，并且能够得出正确的答案。

基于这个想法，人们发明了很多用来计算的机器。最简单的要数只会进行加减法计算的机器了。计算机算是比较复杂的机器。

在日常生活中，我们经常碰到下面的题目，比如说，在一个定量的容器中盛有一种液体，并且装得很满。现在，我们要把液体的一部分倒出来，但是手里只有两只空的容器，它们的容量已知，那么我们应该怎么倒呢？

我们来看一道这样的题目。

有一只水桶，它的容量是12杓（1升等于10合，1合等于10杓），另外两只水桶的容量分别是9杓和5杓。现在，我们往大桶里装满水。那么，如果用这两只空桶来分大桶里的水，怎样才能把平分？

要想解答这个问题，我们不可能真的用水桶来试。其实，我们可以用下面的表格来实现。

在上表的每一栏中，标出了每次倾倒的杓数。

第一栏：空着9杓桶，把5杓桶倒满，也就是说，12杓桶里还有7杓水。

第二栏：把12杓桶里的7杓水倒进9杓桶。

……

我们看到，在这个表中，一共有9栏，也就是说，倒9次就可以解这个题目。

其实，如果变换倾倒的顺序，我们也可以解决这个题目。

你试过之后就会发现，上表中的方法并不唯一，但是如果采取别的方法，倾倒的次数要大于9次。

说到这里，我们可能会有下面的两点想法：

●能否找到一个能适用于倾倒任何容量液体的倾倒顺序？

●能否用两个空容器从第三个容器中倒出任意数量的水？比如说，用9杓空桶和5杓空桶，从12杓桶中取出1杓、2杓、3杓或者11杓水。

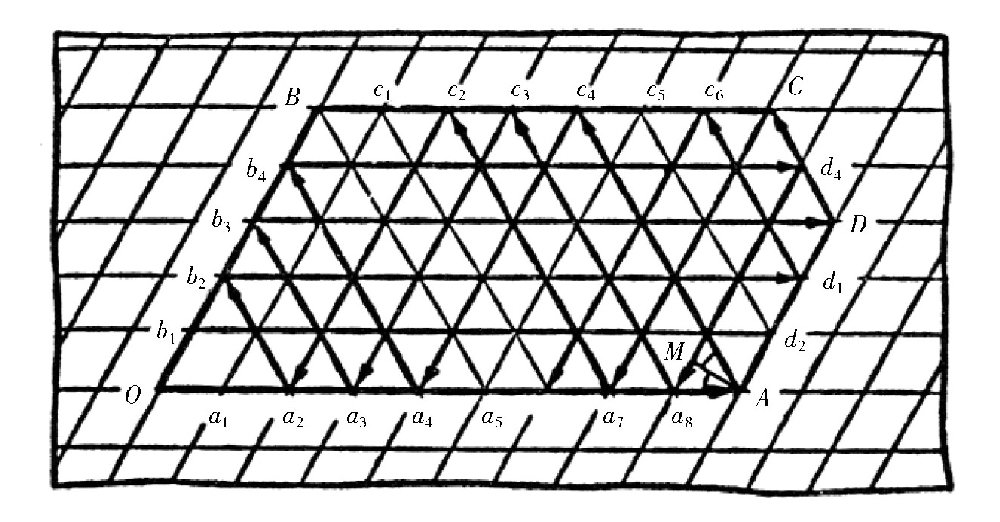
图 “聪明的台球”示意图。

关于上面的问题，只要制造一张结构特殊的台子，台球也可以解答出来。

找一张白纸，在上面画一些斜形的格子，使每个格子都成锐角为60°的菱形，且每个菱形的大小相等。然后，按照图所示的样子画出图形OBCDA。

这样，我们就给台球制作了一张特殊的“台球案”，它的形状就是图中的图形。如果台球在台子上沿着直线OA运动，那么根据入射角等于反射角这一反射定律，∠OAM＝∠MAc₄，所以台球会被边AD撞回来，并且沿着直线AC₄过去，然后在点c₄又撞到边BC，接着沿着直线c₄a₄回来，之后，它会沿着直线a₄b₄、b₄d₄、d₄a₈走……

在前面的题目中，我们一共有三个桶：9杓桶、5杓桶和12杓桶。与此对应，在图中，我们取边OA为9格，边OB为5格，边AD为3（12－9＝3）格，边BC为7（12－5＝7）格。

需要注意的是，图形边上所有的点，都跟边OB或者OA相隔一定的格数。比如说，点c₄跟边OB相隔4格，跟边OA相隔5格；而点a₄跟边OB相隔4格，跟边OA相隔0格（a₄本来就在边OA上面）；点d4跟边OB相隔8格，跟边OA相隔4格，等等。

所以，每当台球撞击边上的每一点，都对应着两个数字。这两个数字中，我们假设其中的一个就是跟边OB相隔的格数，用它表示9杓桶里面的水量，也就是杓数；而另一个数则表示同一个点跟边OA相隔的边数。那么，剩下的水量就是12杓桶中的杓数。

到现在为止，一切准备就绪，我们可以利用这个“聪明”的台球来解答问题了。

把这个台球再次沿边OA打出去，那么，这个台球在碰到每个台边时，就会接着折到另一条台边上，我们不妨这样假设，经过几次跟台边的撞击，它到了点a₆，如果151所示。

第一次的撞击点：A（9；O）。也就是说，第一次倾倒的时候应该按下表来分配12杓桶中的水：

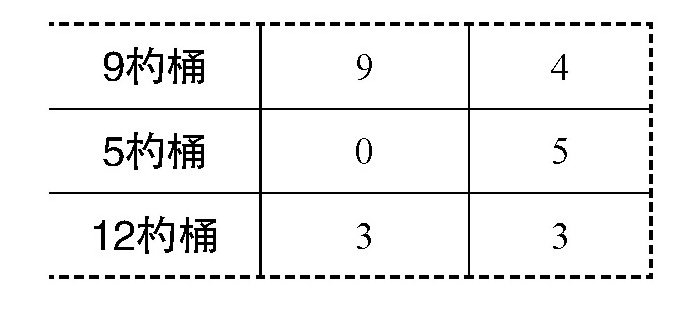
第二次的撞击点：c₄（4；5）。也就是说，第二次倾倒的时候，台球给我们下表中的分配建议：

第三次的撞击点：a₄（4；0）。也就是说，第三次倾倒的时候，应该把7杓桶中的5杓水倒回到12杓桶中：

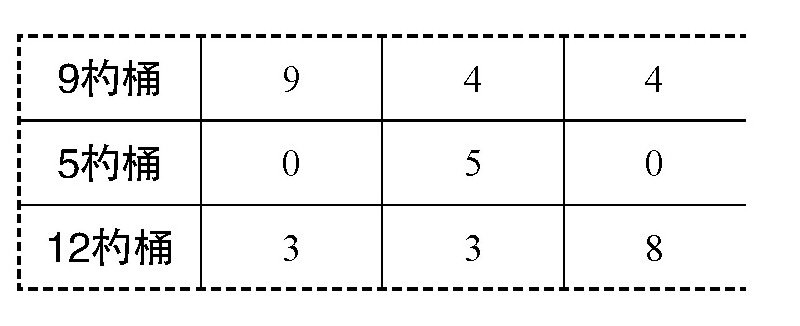
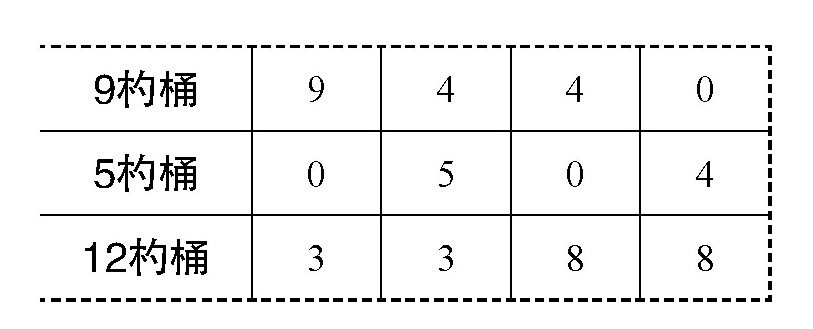
第四次的撞击点：b₄（0；4）。按下表进行分配：

第五次的撞击点：d₄（8；4）；要把12杓桶中的8杓水倒进9杓桶中：

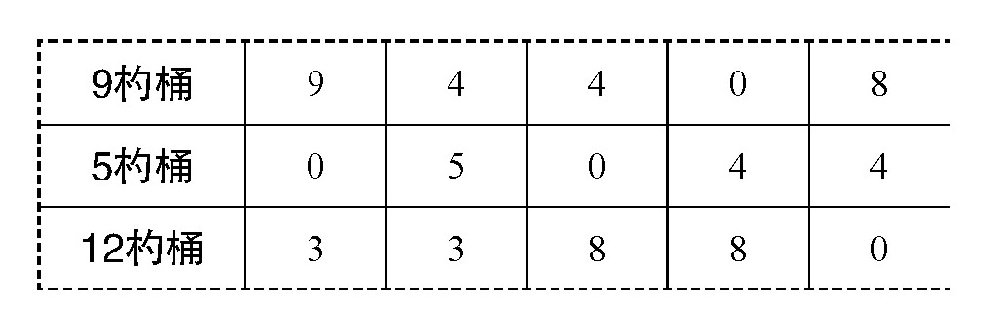
就这样，只要跟着台球走，就可以得到下面的表：

这样，在倾倒了多次之后，完成了题目的要求，在两个桶中都有6杓水。而且，这个问题是台球帮助我们解决的。

不过，跟前面的解答方法相比，台球做得并不好。在前面的方法中，只要过8道手就可以了，但是这里需要过18道手。

其实，有时候台球也可以给我们提供比较简便的方法。如图所示，如果我们让台球沿着边OB打出去，那么根据“入射角等于反射角”这一反射定律，当它沿着边OB来到点B后，就会从边BC折回来，再沿边Ba₅ 滚过去。接下来，会沿着边a₅c₅、c₅d₁、d₁b₁、b₁a₁、a₁c₁走去，最后沿着边c₁a₆ 到达点a₆ 。

可以看到，这里只需要8道手续！

按照上面的假设，如果把台球每一次的撞击点记录下来，我们可以得出下面的表：

也就是说，台球给我们提供了最简便的方法，只要8次程序就可以完成题目的要求。

不过，在有些类似的题目中，可能得不到我们需要的答案。

那么，这时候，台球是如何发现的呢？

很简单：在这种情况下，台球会返回到出发点O，而不是到需要的点上。

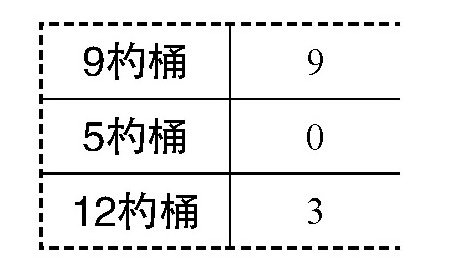
如图所示，这里的桶分别是9杓桶、7杓桶和12杓桶，它给我们的结果是：

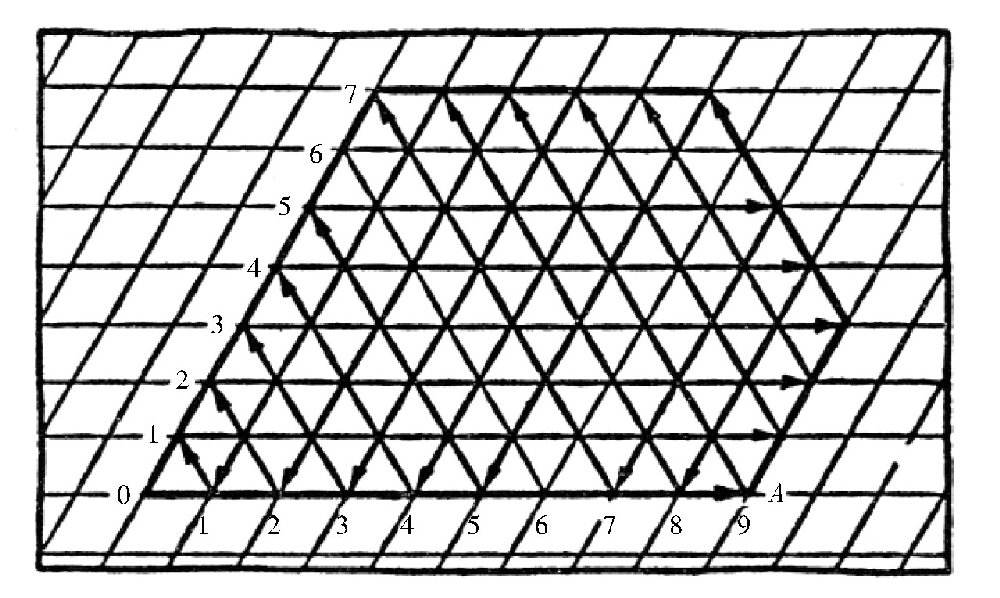
图 “聪明的台球”告诉我们不能用9杓桶和7杓桶从装满水的12杓桶中倒出两份6杓水。

也就是说，这台“机器”告诉我们：用9杓桶和7杓桶，从盛满水的12杓桶里，可以倒出任何杓数的水，除了6杓。

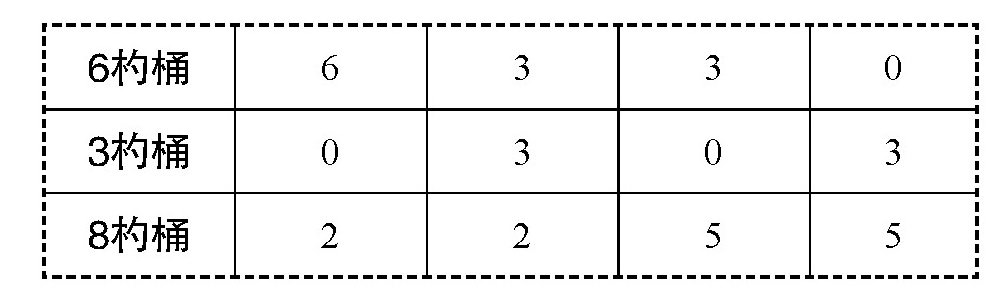
如图所示，如果这三个桶分别是6杓桶、3杓桶和8杓桶，台球只撞了4次边，就回到了出发点O。从下面的表可以看出，也不能从盛满水的8杓桶中倒出4杓水来。

从前面的例子可以看出，在我们设计出的“台球案”上，“聪明”的台球成了一部特殊的计算机，可以解答倾倒的题目。

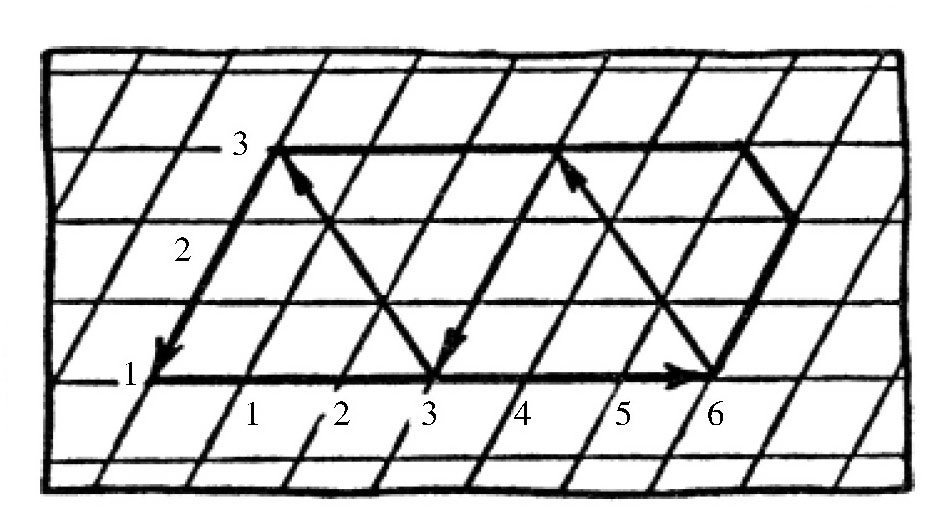
图 解答另一道关于注水的题目。