关于皮球弹跳高度的几个问题

在前文中，我们推导出了关于物体碰撞的一些相关公式。其实，在实际情况下，这些公式并不能直接使用。这是因为，在现实中很难找到“完全没有弹性”或“完全有弹性”的物体。一般的物体都达不到这两种标准。换句话说，对于绝大多数物体来说，它们既不是“完全有弹性”的，也不是“完全没有弹性”的。举个例子来说吧，皮球是什么性质的物体呢？这个问题可能会让古代的寓言家嘲笑我们，不过没关系，我们就是想知道它到底是“完全有弹性”的，还是“完全没有弹性”的。

其实，要想验证一个球的弹性是怎样的并不难，我们可以把它拿到一定的高度，然后让它自然落到坚实的地面上。如果这个球是“完全有弹性”的，那么它落下后再弹起来的高度应该等于原来的高度；而如果是“完全没有弹性”的，那么它就会一点儿都弹不起来。

刚才，我们说的是“完全没有弹性”或“完全有弹性”的球。如果皮球不是完全有弹性的又会是怎样的情况？要想回答这个问题，我们需要先深入研究一下弹性物体的碰撞。当皮球到达地面时，它与地面接触的部分将被压扁，压力会使皮球的速度降低。在这之前，皮球与地面碰撞的情形跟非弹性物体是一样的。换句话说，皮球这时候的速度是u，而失去的速度是v₁-u。但是，刚才压扁的地方又会马上凸起来。由于地面妨碍了它的凸起，所以它必然作用于地面一个力，同时也有一个力作用在皮球上，使得皮球的速度降低。如果皮球的形状得以恢复，皮球形状的变化正好与前面被压扁的情形相反，那么皮球就会再一次失去前面失去的速度，也就是v₁-u。所以，如果皮球是完全弹性的，那它总共减少的速度为2(v₁-u)，它的速度变为：

v₁-2(v₁-u)2u-v₁

如果皮球“不是完全有弹性的”，在外力的作用下，它的形状发生变化后不会完全恢复成原来的样子。换句话说，使皮球恢复成原来形状的力要小于前面使它改变形状的力。与此对应，皮球在恢复形状的过程中失去的速度要比在形状改变的过程中失去的速度小，它的大小等于v₁-u的一部分。如果我们用e表示“恢复系数”，那么皮球在弹性碰撞的整个过程中，前一阶段失去的速度仍然为v₁-u，而后一阶段失去的速度为e(v₁-u)，皮球总共失去的速度就是(1+e)(v₁-u)。于是，皮球碰撞后的速度u₁就等于：

u₁=v₁-(1+e)(v₁-u)(1+e)u-ev₁

这里，我们讨论的是皮球碰撞地面的情形。根据反作用定律，地面在皮球的作用下，速度也会发生变化，可得：

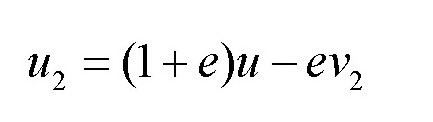
它们的差u₁-u₂得：

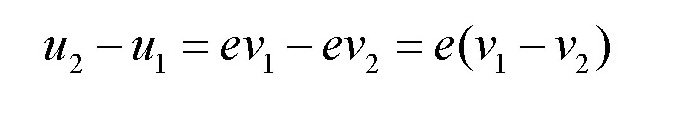
所以，对于皮球来说，恢复系数e得：

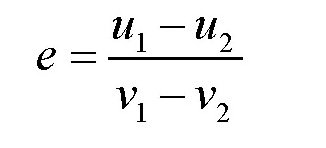
此外，由于这里讨论的是皮球撞向地面的情况，所以u₂=（1+e）u-ev₂=0，v₂=0，那么可得：

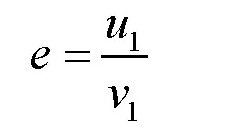
其中，u₁是皮球跳起时的速度，它等于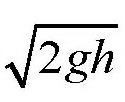

，其中h为皮球跳起的高度；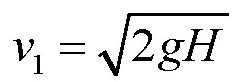

，H为皮球落下的高度。于是可得：

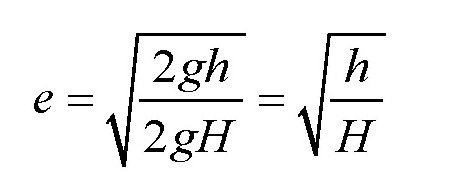
我们推导出了皮球的恢复系数的计算公式。在某种意义上来说，恢复系数e表示皮球“不完全弹性”的程度。从表达式可以看出，只要我们测量出皮球落下的高度，以及跳起来的高度，把得到的两个数值相除，然后再开方，就可以得到我们想要的系数值了。

根据物体的运动规则，当网球从250厘米的高度下落时，它弹起的高度大概是127厘米~152厘米，如 图所示。所以，网球的恢复系数介于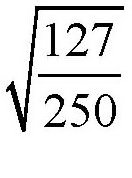

和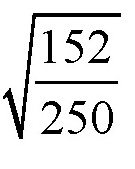

之间，也就是0.71～0.78。

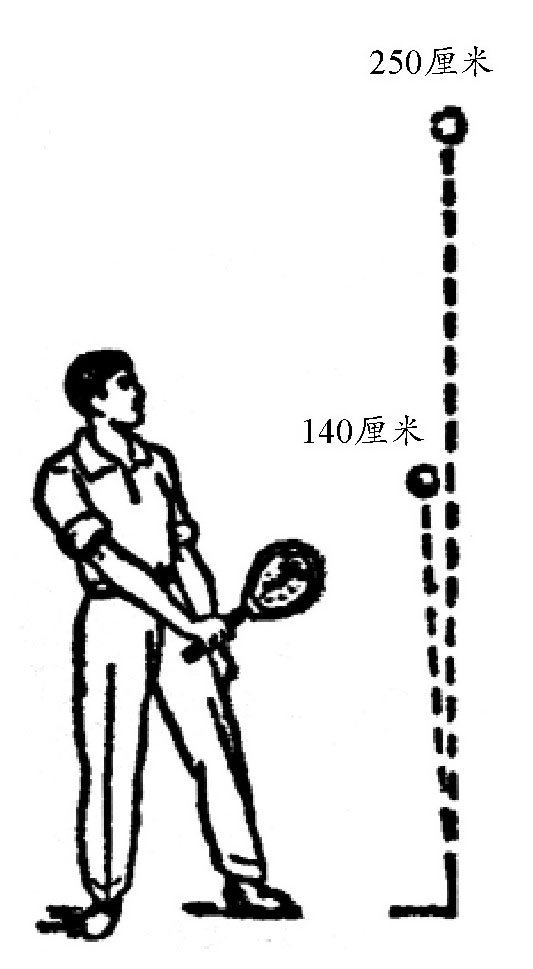
图 网球在从250厘米的高处落下时，能跳起到约140厘米的高度。

下面，我们以e的平均值0.75，即弹性为75％的皮球为例，举几个运动员们非常感兴趣的例子。

第一个例子：让皮球从高度H落下，皮球第二次、第三次以及后面每次弹起的高度都是多少？

通过前面的分析，我们知道，皮球第一次跳起的高度可以用下式来计算：

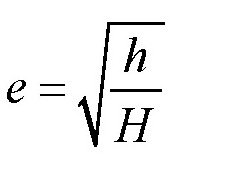
把e = 0.75，H = 250厘米代入上式，可得：

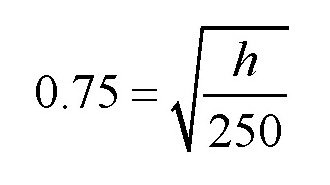
当皮球第二次从地上弹起来的时候，就相当于从h = 140厘米的高度落下，然后再弹起来。假设这时候皮球的高度是h₁，可得：

同样的方法，我们可以求出，当皮球第三次弹起来的时候，它的高度是：

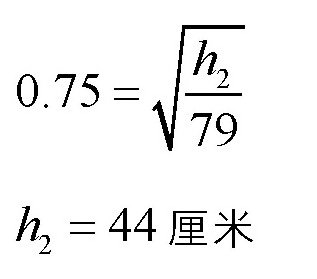
后面每一次的高度都可以用这个方法一直计算下去。

如 图 所示，如果不考虑空气阻力，那么当皮球从埃菲尔铁塔的顶端（高度H = 300米）落下时，它第一次弹起来的高度就是168米，第二次是94米……实际上，由于高度比较高，皮球落下的速度也很大，所以空气阻力的影响是比较大的。

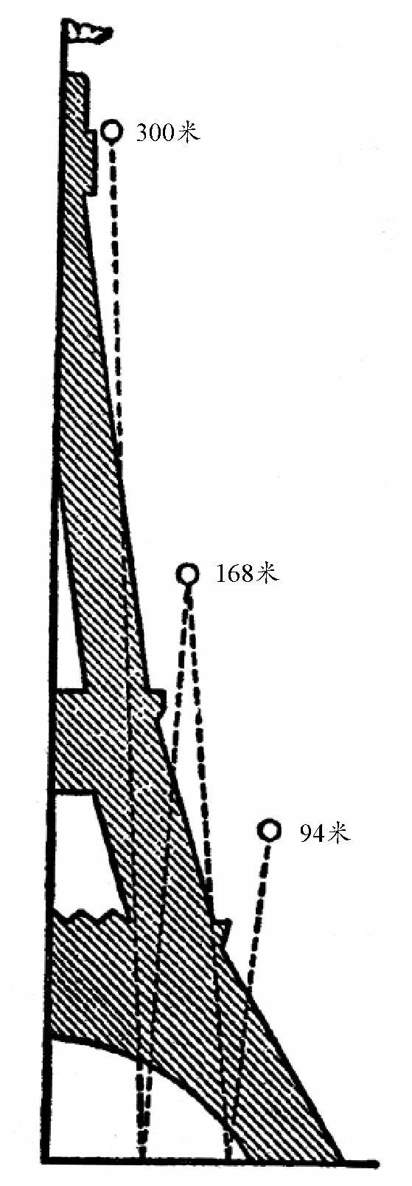
图 从埃菲尔铁塔塔顶落下的球能跳到多高。

第二个例子：如果皮球从高度H落下，那么它弹起来的总时间是多少？

我们有下面的式子：

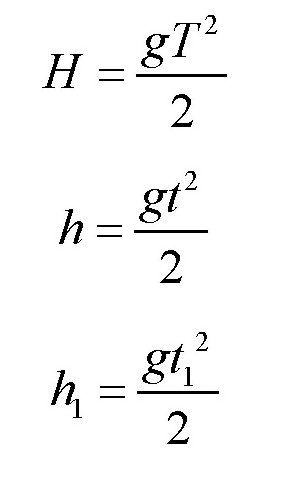
可得：

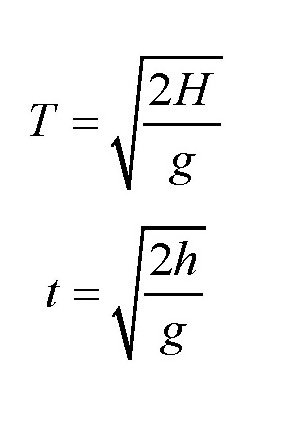
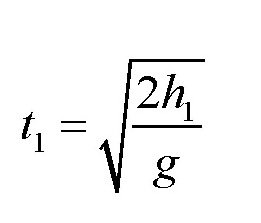
皮球每次弹起来的时间之和就等于：

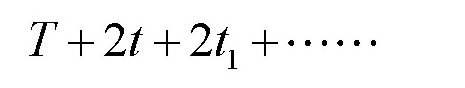
把前面的公式代入，并进行一些计算，我们就可以得到这个多项式之和等于：

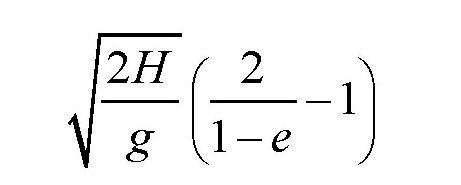
如果H=2.5米，那么把g=9.8米/秒₂和e=0.75代入上式，得到的总时间就是5秒。也就是说，皮球会持续弹跳5秒钟。

如果皮球从埃菲尔铁塔的顶端落下，在不考虑空气阻力的情况下，通过计算可得：皮球会一直弹跳大概1分钟（确切地说，是54秒）。当然了，是在皮球不会撞破的情况下。

如果皮球只是从几米高的地方落下，那它落下时的速度并不大，所以受到的空气阻力也不大。人们曾经进行过专门的试验：让一个恢复系数是0.76的皮球从250厘米的高度落下。我们知道，如果没有空气的阻力，它弹起来的高度应该是84厘米，而实际上，它弹起来的高度是83厘米。可见，这时空气阻力的影响并不大。