直到现在,有一件事情给我留下的印象还非常深刻。在我还很小的时候,曾经看到一个秃顶的人,他手里拿着一个很小的仪器对着一棵很高的松树。他想测量这棵松树的高度。只见他拿起一块方形的木板,然后对着松树瞄了一下。我还以为,这个人会拿着皮尺爬到树上去,可没想到,在做了这些后,他就把那个小仪器放回包里了,然后拍拍手说:“好了,测完了。”可我觉得他根本还没有开始测量呀!
当时,我的年龄还很小,对这个人的测量方法感到非常困惑,不知道究竟是怎么回事,觉得就好像是魔术一样。后来,我上了学,慢慢接触到了几何学,我才知道,这其实根本不是魔术,原理也很简单。测量树根本不需要进行实际的测量,只需要运用几种简单的仪器就可以了,而且方法有很多种。
在公元前6世纪,古希腊哲学家泰勒思发明了一个方法,也是现在被认为最古老、最容易的方法。当时,他用这种方法来测量埃及金字塔的高度。在测量金字塔高度的时候,他利用了金字塔的影子。当时,包括法老和祭司在内的很多人都聚集到了一起,就是为了看一下这位哲学家是怎么测量高大的金字塔的。据说,当时泰勒思选择了一个特殊的时间,在那个时间,他自己的影子长度正好跟自己的身高相等。这样,只要测量出金字塔影子的长度就可以了,因为这个长度正好也等于金字塔的高度。只不过,金字塔影子的长度要从塔底的正中心计算,而不是从金字塔的边缘计算。泰勒思正是从自己的影子中得到了灵感,发明了这个方法。

现在,对于这位哲学家发明的这个方法,即使是小孩子,也很容易明白其中的道理。但是,我们不得不承认,是因为我们学了几何学这门学科,才做到的。在当时,可没有几何学。大约在公元前300年,古希腊数学家欧几里得写过一,对几何学进行了系统的论述,直到今天,还被我们学习运用。对于现在的中学生来说,的很多定理都非常简单,但是在泰勒思那个时代,还没有这些定理。而在测量金字塔高度的过程中,必须利用到其中的一些定理,也就是下面的这些三角形特性:
●等腰三角形的两个底角相等。反过来,如果三角形有两个角相等,那么这两个角的对边也相等。
●对于任意一个三角形,它的内角和等于180°。
泰勒思发明的测量高度的方法,正是建立在三角形的这两个特性之上的。当影子的长度等于他的身高时,就说明太阳照向地面的角度正好等于直角的一半,也就是45°。这时候,金字塔的高度和影子的长度正好是一个等腰三角形的两条边,所以它们是相等的。
如果天气比较好,在太阳的照射下,大树便会有影子。这时,便可以利用这种方法来测量大树的高度。不过最好是独立的大树,否则,它们的影子会重合,不便测量。但是,如果是在纬度比较高的地方,这个方法并不是很好用。这是因为,在这些地方,只有在夏天中午很短的一段时间里,影子的长度才会跟物体的高度相等。所以说,并不是所有的地方都可以用到这个方法。
不过,在这种地方,我们可以把这个方法改进一下,只要有影子就可以得到物体的高度。这时,需要做的工作就是,先分别测量出物体的影子和自己的影子的长度,然后利用下面的比例关系计算出物体的高度,如图所示。
AB∶ab=BC∶bc
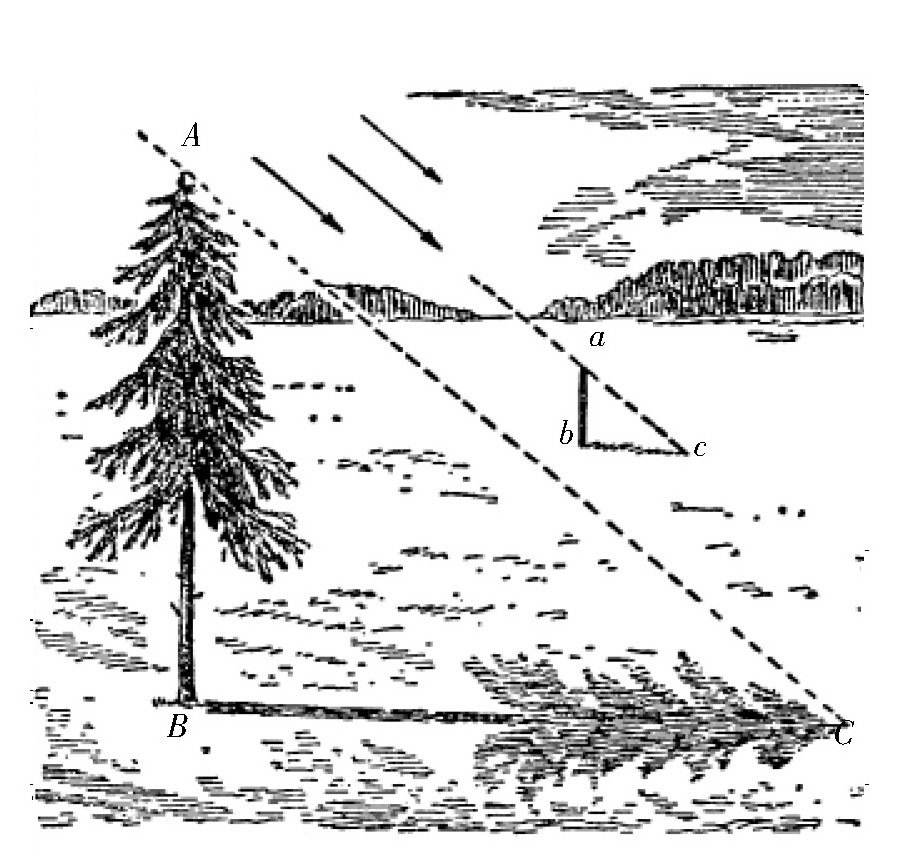
图 利用阴影的长度来测量树的高度。
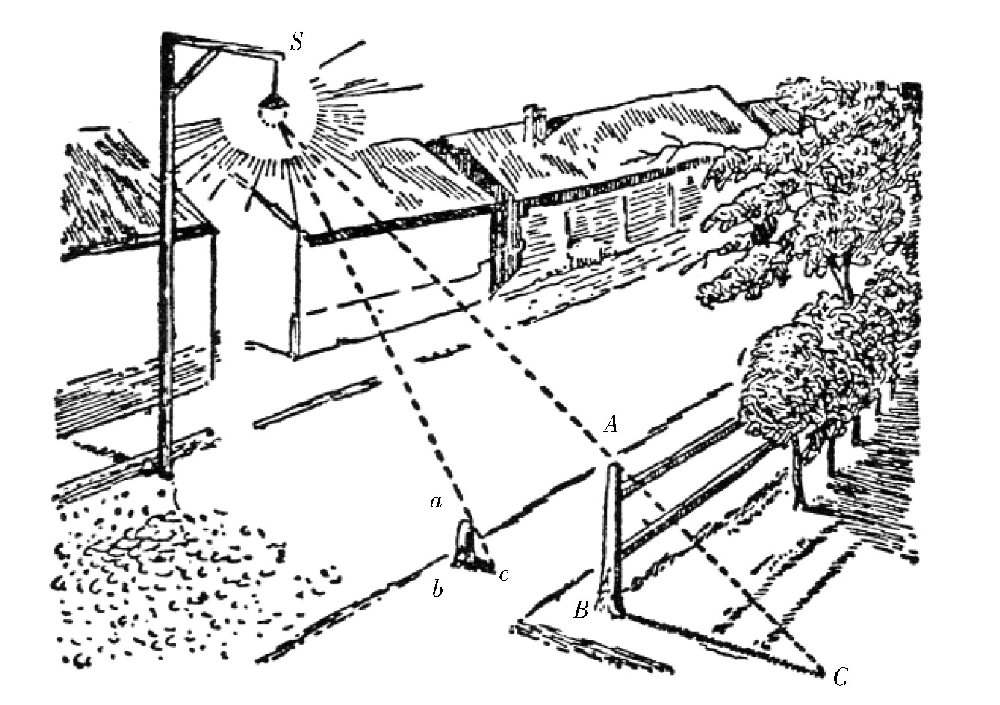
图 为什么在路灯下这种测量方法不适用?
这个关系之所以成立,也是利用了几何学中的知识,如果两个三角形ABC和abc相似,那么它们的对应边就是成比例关系的。所以,物体的影子长度与身体的影子长度的比值,就等于物体的高度跟身高的比值。
你可能会疑惑,这么简单的道理,还需要用几何学来证明吗?如果没有几何学,难道我们就没有办法得到物体的高度了吗?其实,事实就是这样的。如图所示,如果把刚才的方法运用到路灯以及它所形成的影子上,就不适用了。从图中可以看出,柱子AB的高度是矮木桩的3倍,但是它们的影子BC和bc却不是3倍的关系,而是差不多8倍的关系。如果没有几何学,要想充分解释这个方法的原理,并且说明为什么这个方法在此时行不通,是很难的。
【题目】为什么这个方法对路灯的影子就不适用了呢?跟前面测量大树的情形有什么区别?我们知道,我们都把太阳照射出来的光线看作是平行的,而路灯就不一样了,从路灯发出的光线并不平行,关于这一点,从图中我们可以很明显地看出来。那么,为什么太阳发出的光线是平行的呢?太阳光不也是从同一个太阳发出来的吗?
【解答】我们之所以把太阳发出的光线看作是平行的,是因为从太阳发出的光线间的角度极小,几乎可以忽略。关于这一点,我们可以用几何学的知识进行证明。假设从太阳上发出了两条光线,照射到地球上的某两个点,不妨假定这两个点的距离有1000千米。如果我们有一个巨大的圆规,将其中的一只脚放到太阳的位置,另一只脚放到刚才的其中一个点上,画一个圆。很显然,这个圆的半径正好是地球到太阳的距离,也就是150000000千米。换算一下,很容易得到这个圆的周长,它等于:
2×π×150000000≈940000000(千米)
刚才选取的两点间的距离是1000千米,也就是圆上的一段弧长是1000千米的弧。我们知道,在圆周上的每一度对应的弧长都是圆周长的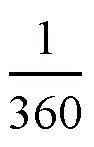
。换算一下,也就是:
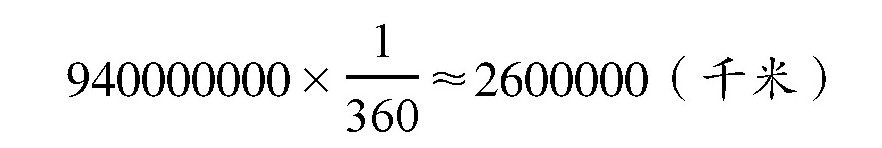
每一分的弧长就是这个数值的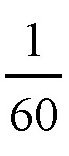
,约为43000千米,每一秒的弧长又是这个数值的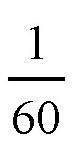
,即720千米。
我们刚才提到的弧长只有1000千米,也就是说,它对应的角度是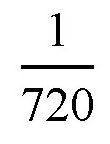
秒,这个角度几乎可以忽略不计,即便是用精密的仪器,也很难测量出这么小的角度。所以,在地球上看来,太阳发出的光线完全可以看作是平行的。
需要说明的是,太阳照射到地球直径两端的光线之间的夹角大约是17秒,这个角度可以用仪器测量出来,科学家也正是利用这个角度才计算出地球与太阳之间的距离的。
由此可见,如果没有几何学的知识,对于前面提到的测量高度的方法,
我们根本没有办法解释。
不过,在实际运用这个方法进行测量的时候,并不是一件容易的事情。这是因为影子边缘的分界线并不是十分分明,所以在测量影子的长度的时候,就很难测量准确。太阳照射到物体上的时候,形成的影子边缘会有一个轮廓,这个轮廓呈现出的是半影,这就使我们很难准确地找到影子的边缘。之所以会产生半影,是因为太阳这个发光体太大了,光线不是从一个点上发出来的。如图所示,树的影子BC在边缘处会多出来一段若隐若现的半影CD。实际上,半影CD的两端与树梢形成的夹角CAD与我们看向太阳直径两端形成的夹角是相等的,这个度数大约是半度。即使是在太阳的位置比较高的时候,也会存在半影,所以这时候就会产生测量误差。有时候,这个误差可能会达到5%,甚至更多。再加上其他因素的影响,比如,地面凹凸不平,就会导致误差更大。所以,如果在丘陵地带,这个方法是不适用的。
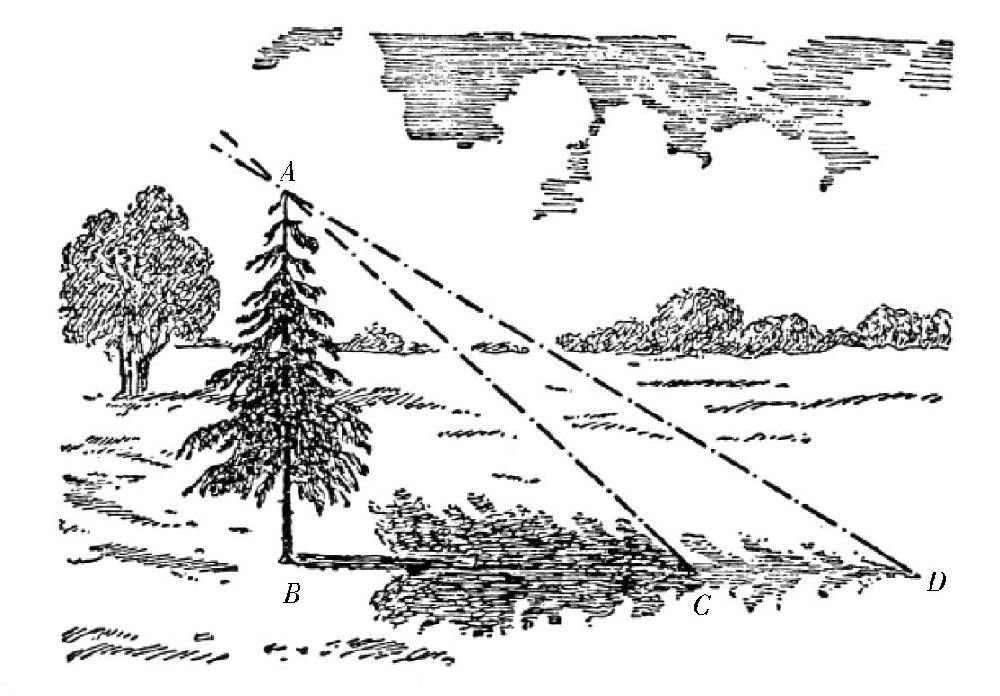
图 半影是如何形成的?
