在本章中,我们要学习的是仅仅根据正弦函数的概念,不用公式和函数表,就可以计算出任何一个三角形的边长,并且精确到2%,内角的计算可以精确到1°。比如,在郊游的时候,你身边没有函数表,并且忘记了计算的公式,就可以用这里的方法。如果鲁滨孙也知道这种方法,就可以解决他遇到的很多问题了。

现在,我们假设你根本没有学过三角学,或者你学过,但是已经忘得一干二净了。我们先从最简单的计算开始。在一个直角三角形中,其中一个锐角的正弦值怎么计算呢?其实,它就等于这个角的对边跟三角形的弦的长度之比。比如,在图(a)中,角a的正弦就是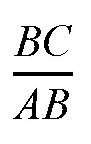
,或者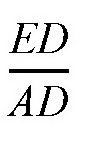
,或者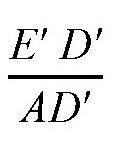
,或者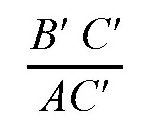
。利用相似三角形的性质,我们知道,它们都是相等的。
如果没有函数表,从1°到90°各个角度的正弦值怎么计算呢?其实方法很简单:我们可以自己编一个函数表。下面,我们就来学习一下。
在几何学中,我们已经知道一些正弦值的角度,比如,角度如果是90°,那么它的正弦值等于1,那么45°角呢?根据勾股定理,我们可以很容易得出,它的正弦值等于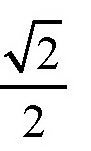
也就是0.707。如果是30°,这个角的对应边的长度等于直角对应边的一半,所以它的正弦值就是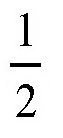
。这三个角的正弦值就是下面的式子:
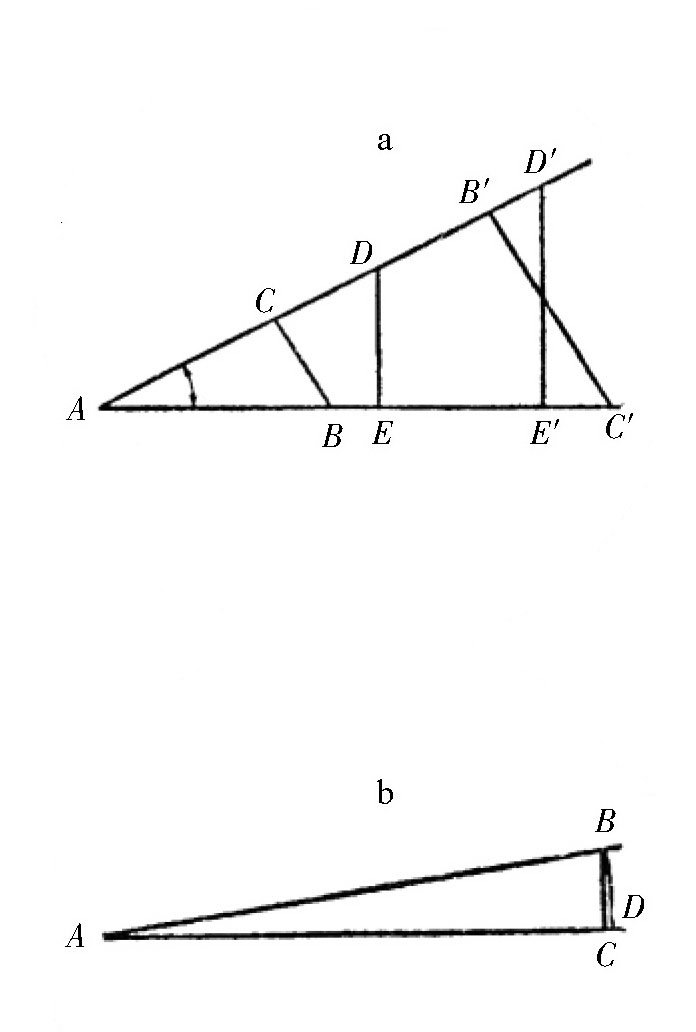
图 直角三角形中一个锐角的正弦函数。
sin30°=0.5
sin45°=0.707
sin90°=1
当然了,如果只知道这三个角的正弦值,要想解答几何学上的题目,是根本不够的,我们还需要知道中间一些角的正弦值。如果这个角的角度很小,那么在计算的时候,就可以利用弧长跟半径的关系来代替对边和弦,这样的误差也会比较小。在图(b)中,我们可以看到,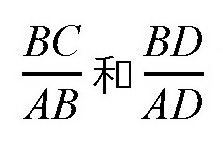
相差很小,而后面这个比值很容易计算出来。比如,1°角对应的弧长BD是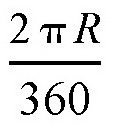
,所以,sin1°可以用下面的式子计算:
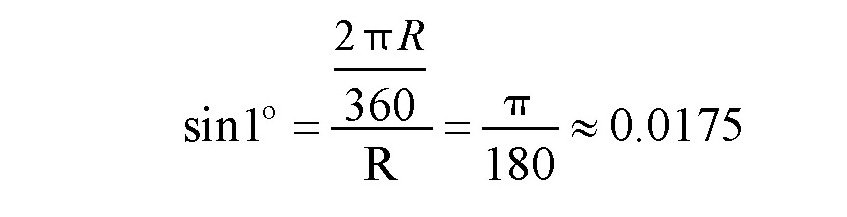
运用同样的方法,我们可以得出:
sin2°=0.0349
sin3°=0.0523
sin4°=0.0698
sin5°=0.0872
不过,需要指出的是,这一方法只适用于角度较小的正弦值求法,如果角度较大,误差就会比较大了。
比如,我们用这个方法来求sin30°,那么得出的正弦值就是0.524而不是0.500,也就是说,误差是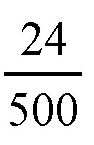
,已经达到了5%。
利用这种方法,我们来计算一下它的界限。如果用精确的方法计算sin15°的值。如图所示,我们做一个这样的图。假设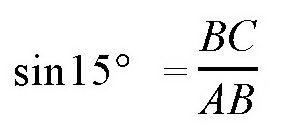
。延长BC到点D,使CD=BC,连接点A和点D,三角形ADC和三角形ABC是全等三角形,而且,角BAD等于30°。然后,再从点B引一条垂线BE相交于AD,则三角形BAE是直角三角形。其中,角BAE等于30°,所以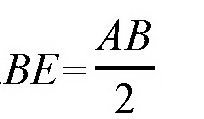
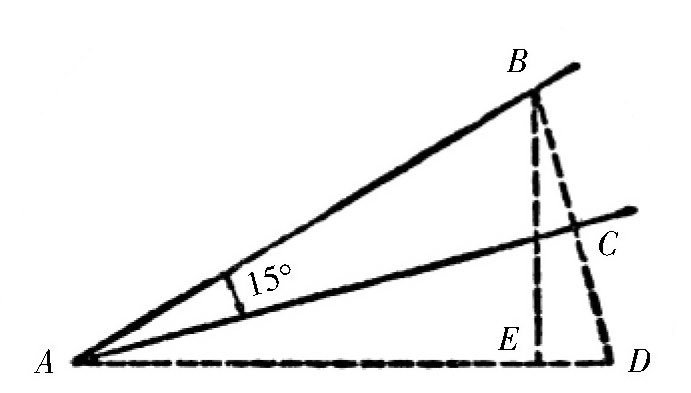
图 求出sin15°的方法。
根据勾股定理,我们可以根据下面的式子求出AE:
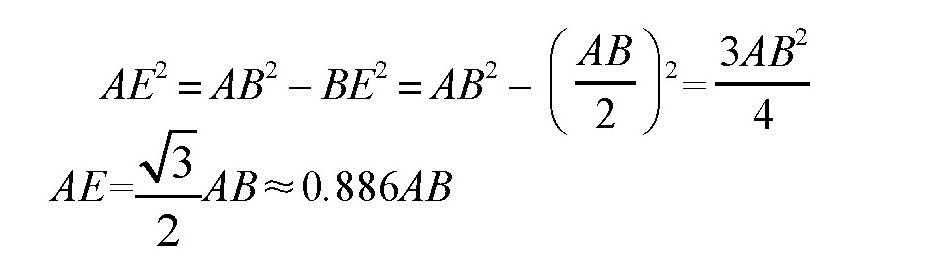
所以:
ED=AD-AE=AB-0.866AB=0.134AB
在三角形BED中,我们有:
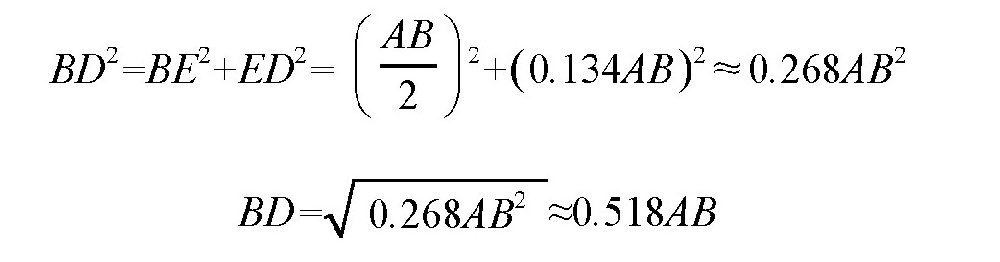
而BC的大小是BD的一半,也就是0.259AB,所以,我们可以得到:
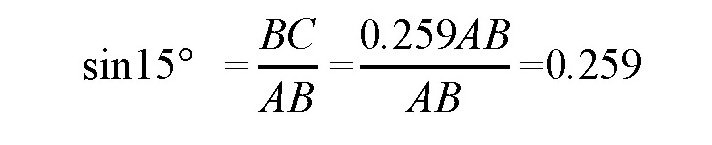
在函数表中,sin15°的值就是这个数值,如果用刚才的方法,得到的数值是0.262,如果取前两位数,都是0.26。跟0.259比起来,这个数值的误差是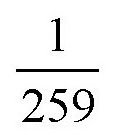
,也就是大约0.4%。所以,如果角度在1°~15°,都可以用前面的方法计算出它们的正弦值。如果角度在15°~30°,它们的正弦值可以用比例关系计算。比如,sin30°跟sin15°的差值是0.5-0.26=0.24,所以我们可以认为,角度每增加1°,正弦值就会相差这个数的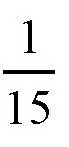
,也就是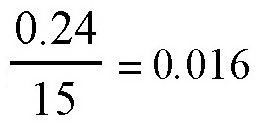
。从严格意义上说,这个关系并不精确,但是误差一般体现在第三位小数上,通常我们只取前两位小数,所以还是可以满足我们的要求的。根据这个方法,我们可以得到:
sinl6°=0.26+0.016≈0.28
sinl7°=0.26+0.032≈0.29
sinl8°=0.26+0.048≈0.31
sin25°=0.26+0.16≈0.42
……
在上面的这些数值中,前两位小数都是准确的,完全满足我们的要求,跟真实值相比,它们的误差都小于0.005。
如果角度在30°~45°,也可以这么计算。我们知道,sin45°-sin30°=0.707-0.5=0.207。把它除以15,等于0.014。把它分别加到30°的正弦值上,我们可以得到:
sin31°=0.5+0.014≈0.51
sin32°=0.5+0.028≈0.53
sin40°=0.5+0.14≈0.64
……
这样,我们就得到了45°以下角度的正弦值了。根据勾股定理,我们就可以求出大于45°的锐角的正弦值。比如,要求出sin53°的值,也就是图中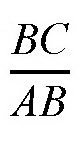
的值。在图中,角B等于37°,所以利用前面的方法,我们可以得出它的正弦值是0.5+7×0.014=0.6,而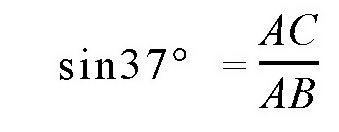
,也就是AC=0.6AB,那么,BC的长度就是:
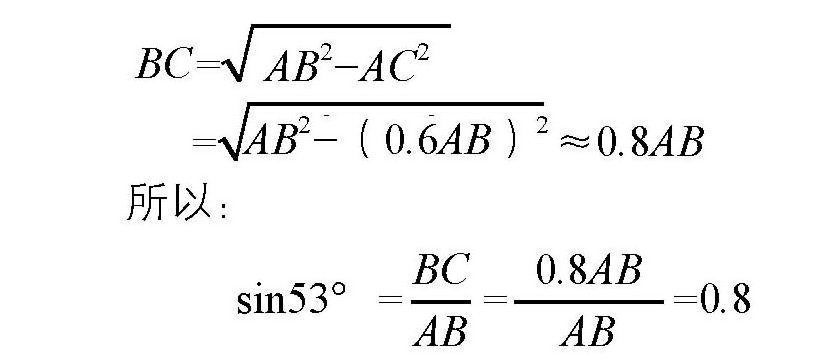
只要会开平方根,这样的计算会变得很简单。
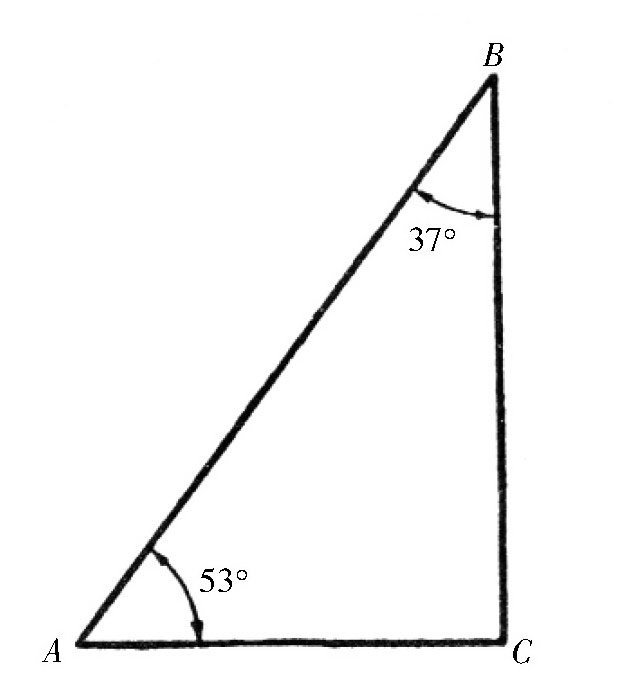
图 以上角的正弦函数值。
