我们来看一个非常有趣的杂技,人们通常称它为“肉弹表演”,它的表演方式是这样的:将一个人放进炮膛里。从炮口把这个人发射出去。这个人在空中划出一道弧线,然后落到距离炮膛30米的一个网上,如 图 所示。
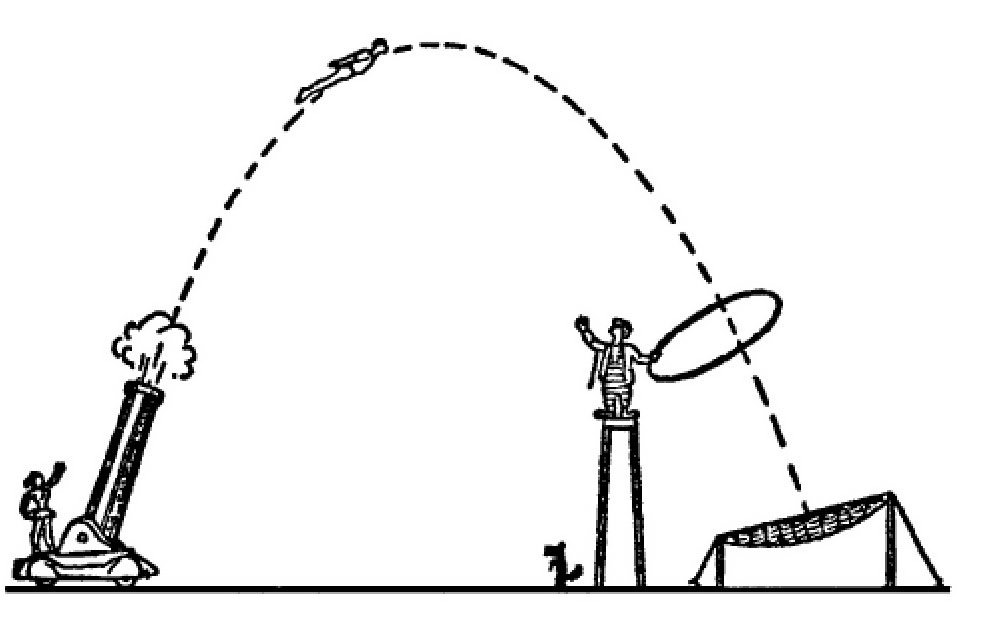
图 “肉弹表演”。
需要注意的是:这里提到的炮和发射都应该加上引号。其实,它们都不是真的炮,而且也不是真的发射。当表演这个杂技的时候,我们确实会看到炮口冒出一股浓烟,但实际情况是,人并不是真的被炮膛里的火药给轰出去的。这股浓烟只是为了营造更加逼真的效果。实际上,把人抛出去的是弹簧,在人被弹簧抛出去的同时,点燃事先放在炮口的可以释放浓烟的物品,于是我们就产生了错觉,好像这个人真的是从炮膛里发射出去的一样。
在 图 中,标出了这个杂技的一些数据。这些数据是著名的“肉弹表演”的表演者莱涅特做了大量实验后得到的:
●炮筒的倾斜度:70°。
●“肉弹表演”的表演者的飞行最大高度:19米。
●炮膛的长度:6米。

图 “肉弹表演”图解。
在表演这个杂技的时候,参与表演的人,也就是“肉弹”,会感受到一些奇怪的变化。在被发射的瞬间,他会感到身体被什么东西压住了一样,好像自己的体重一下子增加了。从炮膛里发射出去后,他会感觉好像没有了任何体重。最后,当落到网上的瞬间,他又感觉自己的体重猛然增加了很多。对于参与者来说,所有的这些感觉并不会对他的身体健康造成什么危害,完全在他的承受范围内。需要指出的是,对于宇航员来说,也会体会到这种感觉。所以,从某种意义上来说,对这一情形的研究是非常有意义的。
我们知道,宇宙飞船也是靠发动机升上空中的。在飞船没有达到一定速度之前,飞船里面的宇航员也会感觉自己的体重在增加。当发动机关闭、飞船进入轨道后,宇航员又会感觉自己的体重完全消失了,也就是失重了。在苏联发射的第二颗人造地球卫星上,人们把一只狗放了进去。这只狗也经受了同样的感觉,并活了下来。
下面,让我们回到刚才的表演中。
当参与表演的演员在炮膛里还没有发射出去的时候,他到底经受了多大的压力呢?换句话说,增加在他身上的重力到底有多大呢?其实,这个数值的大小是可以计算的,只要知道了这个演员在炮膛里发射时的加速度,就可以求出来了。通过前面的学习,我们知道,要想知道这个加速度的大小,就需要知道演员在炮膛里走过的距离,也就是炮膛的长度,以及演员在从炮膛里发射出去的瞬间得到的速度。在前文中,我们已经知道了炮膛的长度为6米,那么速度呢?其实,速度也可以计算出来。在前文中我们知道:这个演员飞行的最大高度是19米,所以根据前面一节得出的公式可得:
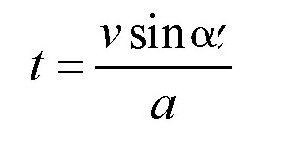
其中,t 为这个演员上升过程中所用的时间,v 为发射出去时的速度,α为炮膛的倾斜角,a 为加速度。
此外,我们还知道下面的公式:
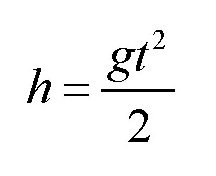
这里的h为演员上升的高度。
可得:
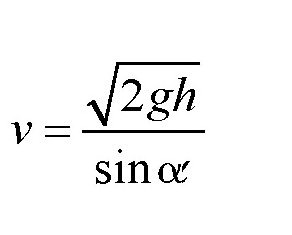
其中,式子右边的各个数值都是我们知道的。这里,g=9.8米/秒2,而从图中我们知道:h=19米,所以速度为:
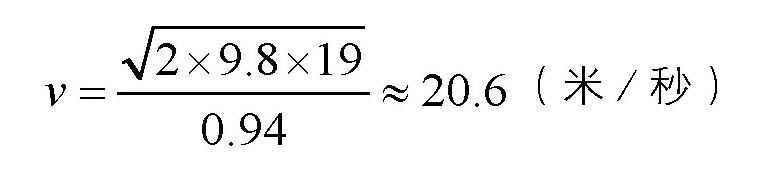
也就是说,演员从炮膛里发射出去时的速度是20.6米/秒。通过下面的式子:

我们就可以求出演员在炮膛里得到的加速度是:
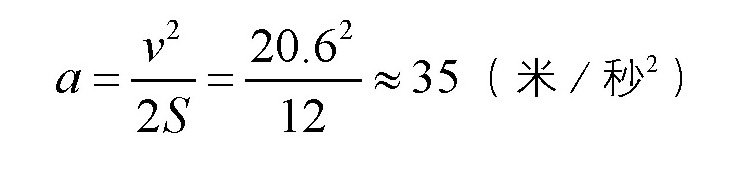
这个加速度的大小差不多是重力加速度的
倍。也就是说,除了演员自身的体重,他的身上又加上了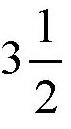
倍的自己的体重,所以他会感觉到自己的体重增加到了原来的
倍。
那么,对于演员来说,体重增加的过程会持续多长时间呢?我们可以通过下面的公式计算得到:
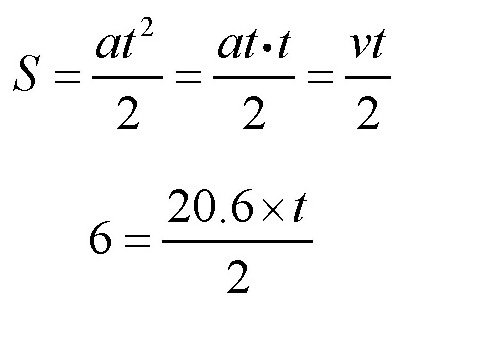
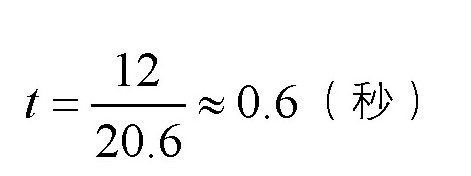
也就是说,这个演员在半秒多钟的时间里,会感觉自己的体重增加了很多。如果这个演员的体重是70千克,那么他感受到的自己的体重将是300千克。
下面,我们不妨来深入研究一下这个有趣的杂技。当演员从炮膛里被发射出去之后,他会在空中飞行一段时间,在这段时间里,他感觉自己的体重完全失去了,那么这段时间究竟有多长呢?
在前文中,我们知道,计算演员飞行时间的公式为:
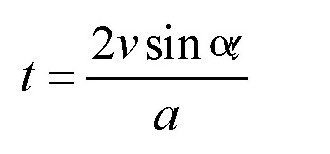
把前面的各项数值代入,可得:
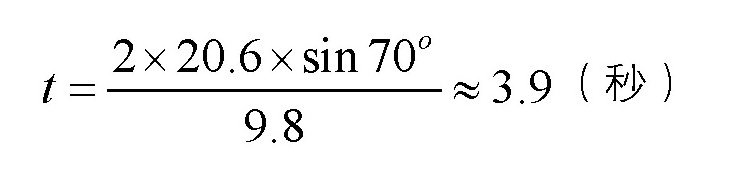
也就是说,演员感觉失重的时间大概持续了4秒钟。
在前面的分析中,我们知道,当演员落到网上的时候,他感觉自己的体重又增加了,那么,这时增加的体重又是多少呢?持续的时间有多长呢?
我们也可以运用同样的方法求出来。如果网的高度和炮口的高度一样,那么演员落到网上的速度跟发射出炮膛时的速度是一样的。但是,在图中,网的高度要比炮口低一些,所以演员落在网上的速度要稍微大一些,不过两者的差别很小。为了使计算不过于复杂,我们这里假设这个差别可以忽略不计。那么,演员到达网上时的速度就是前面计算得出的20.6米/秒。我们已知:演员落到网上的陷下去的深度是1.5米。也就是说,演员以20.6米/秒的速度下落1.5米后速度变为0。假设演员在这个过程中的加速度不变,根据公式:
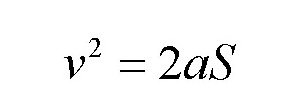
可得:

可得:
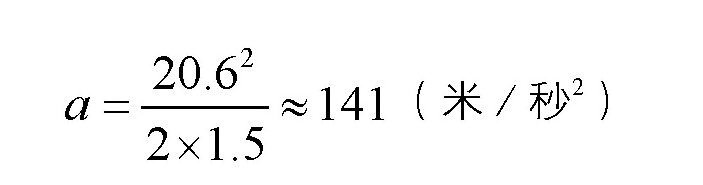
由此可见,演员在落到网里的时候,加速度约为141米/秒2,这个数值大概是重力加速度的14倍。也就是说,在从他落到网上到速度变为0的那段时间里,他会感觉自己的体重增加到了原来的15倍。幸亏这种非同寻常的感觉只持续很短的时间,否则哪怕是受过再多次训练,这种感觉也是难以承受的,会把这个人压死,因为人的肌肉力量是有限的,根本承受不了这么大的重力。
