前面我们讲到,不用爬到树上,一样可以测量出大树的高度。那么换一种情况,如果有一条河,不渡过河去,是不是也可以测量出它的宽度?从几何学的原理上来说,这是可能的。跟测量大树一样,我们可以采取同样的方式,构造几何图形,用其他可以测量的距离把河的宽度计算出来。
其实,这样的方法也有很多,下面,我们挑选几种比较简单的方法讲解一下。
方法一:三针仪测距法
在这个方法里,我们要用到如图所示的三针仪。这个仪器制作起来其实很简单,只要在一块木板上画一个等腰直角三角形,然后分别在3个顶点上钉上一个大头针,仪器就做成了。

图 三针仪测距法。
如图所示,我们站在河岸的点B上,要测量河的宽度,也就是AB的长度。下面开始测量。
首先,我们站到河岸上的点C处,把三针仪放在眼睛的前面,闭上一只眼睛,用另一只睁开的眼睛看向BA,使这两个点正好跟三针仪上的a、b两点在一条直线上。这时,我们的站立点正好在AB延长线上。
其次,保持三针仪位置不动,用眼睛看向b、c两点的方向,找到点D,D点正好被大头针b、c挡住。这时,线段DC跟线段AB是垂直的。再次,我们在C点上钉一个小木桩,然后带着三针仪沿着直线CD走到点E,如图所示,使大头针b正好挡住C点的木桩,大头针a正好挡住点A。这样,我们就找到了一个三角形ACE,而且,角C是直角,角E等于角A,都是45°,所以,AC等于CE。

图 用三针仪确定第一个位置。
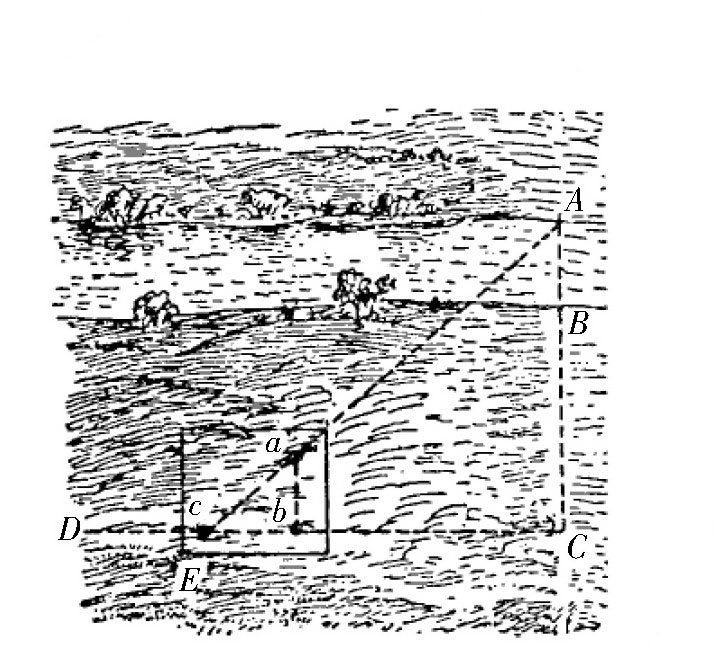
图 用三针仪确定第二个位置。
只要测量出CE的距离,就得到了AC的长度,然后再减去BC,就可以得出河的宽度AB了。
在实际测量的过程中,很难保证三针仪静止不动,所以可能会引起较大的误差。最好的方法是把三针仪水平固定在一根木杆的上端,然后把木杆底端插到地里。
方法二:全等三角形测距法
这种方法跟第一种方法有一些近似的地方。
首先,在AB的延长线上找到点C,然后,站到点C处,在点C找出垂直于AC的直线CD。到这里,跟方法一是一样的,不过后面就不同了。
其次,如图所示,在直线CD上,随便找一个点F,然后在CF的正中间位置,我们记为点E。那么,很显然,CE等于EF,分别在点E和点F处插上一个小木桩。
再次,在点F处找到垂直于CF的垂线FG,沿着FG的方向前进,找到点H,使得从点H看向点A的时候,点A正好被点E的小木桩挡住,即点H、E、A在一条直线上。
最后,利用全等三角形的性质,我们就可以得出:FH=CA。然后,从线段FH中减去线段BC的长度,就得到了河的宽度AB。
相比于方法一,这种方法的适用范围更广一些。而且,如果地形允许的话,可以分别用这两种方法进行测量,以检验测量结果的准确性。

图 全等三角形测距法。
方法三:相似三角形测距法
其实,对于方法二,我们还可以做一些改进。在直线CD上,不是找出相等的两段,而是找出另外一个点E,点E要满足这样的关系:CE=4EF,也就是说,CE的长度是EF长度的4倍,如图所示。后面的计算方法跟前面是相同的,沿直线FC的垂线方向EG找出点H,使得从这一点看向点E的时候,正好挡住点A。只不过,这里的FH不等于AC,而是AC的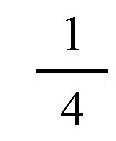
。这是因为,图中的三角形ACE和EFH是相似三角形,而不再是全等三角形了。利用下面的比例关系:
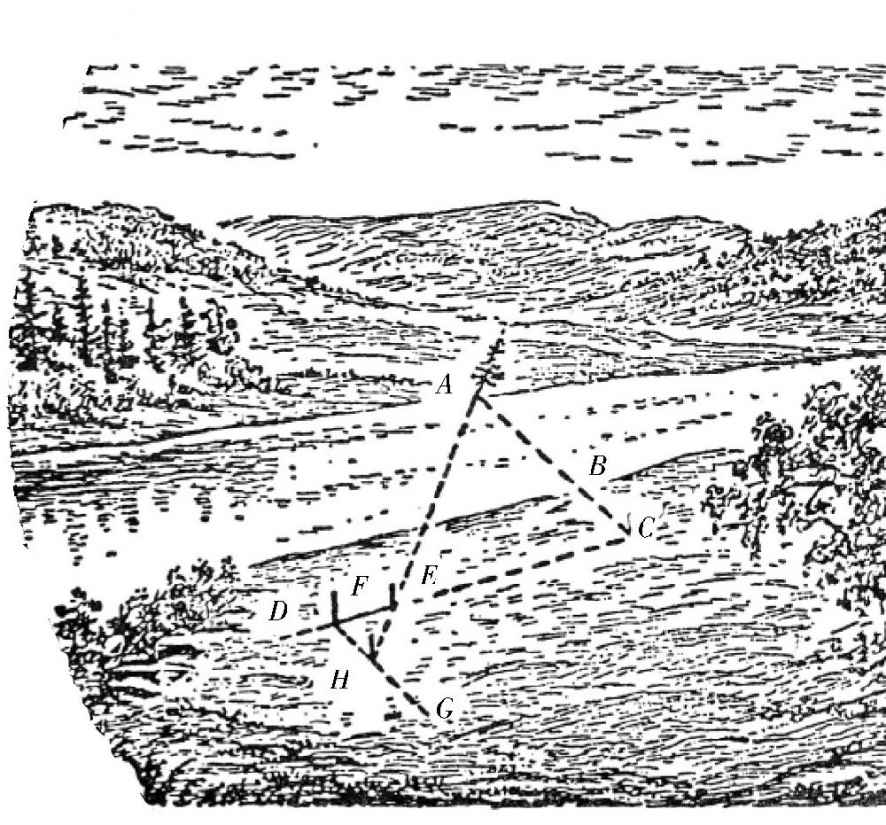
图 相似三角形测距法。
AC∶HF=CE∶FE=4∶1
就可以求出线段FH的长度,乘以4就是AC的长度,再减去线段BC的长度,就可以得到河的宽度AB了。
相比于方法二,这种方法的好处就在于,不需要太大的地方,就可以完成测量,并计算出河的宽度。
方法四:直角三角形测距法
这种方法利用了直角三角形的性质:如果一个直角三角形有一个锐角是30°,那么跟这个锐角相对的一条直角边的长度正好等于这个直角三角形斜边的一半。这一性质很容易就可以证明,下面我们就来证明一下。

图 当直角边等于斜边的一半时。
如图所示,直角三角形ABC的角B等于30°,AC是这个三角形的斜边,AB和BC分别是三角形的两条直角边。从图中可以看出,如果我们以BC为轴,把三角形ABC转到另一边,那么就会形成一个新的三角形ABD。由于点C两边的两个角都是直角,所以点A、C、D在一条直线上。很明显,在三角形ABD中,角A等于60°,角ABD是由两个30°的角合在一起的,所以也是60°。由等腰三角形的性质,我们可以得出:AD=BD=AB。而AD=2AC。反过来,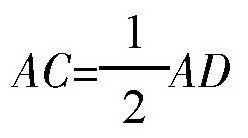
。
知道了这个性质,我们就可以用它来测量河的宽度了。
这里,我们需要用到一个特殊的三针仪。在这个三针仪上,三角形不是等腰直角三角形,而是像图中的三角形ABC一样,其中的一个直角边长度等于斜边的一半,如图所示。
制作好这样的三针仪后,我们带着它来到图中的点C,使AC方向正好跟三针仪上的斜边重合。朝着三角形较短的一条直角边望过去,找出CD的方向。利用三针仪,在CD上找出点E,使EA的方向正好垂直于CD。那么,30°角对应的直角边EC就等于AC的
。所以,只要测量出CE的长度,再乘以2,然后减去BC,就得出要求的河面宽度AB了。
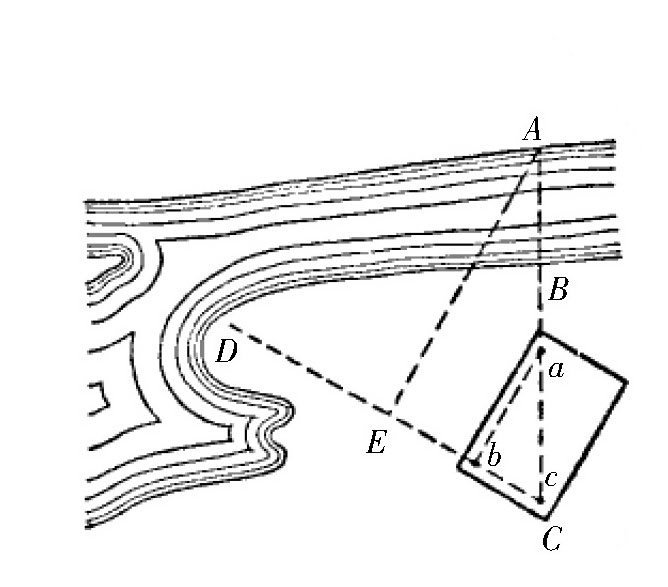
图 直角三角形测距法。
