关于这个问题,很多人会怀疑它是否真的能实现。走的路比较远,而花的时间却比较少,怎么可能?这确实是可能的,只要我们安排合理,在走路的时候,根据不同的路况选择不同的行进速度,就可以实现。
举个例子,一个人正好住在两个车站之间,并且离其中的一个车站近一些,离另一个远一些。如果他想到比较远的车站,他可以走到离他较近的车站,再反方向乘坐火车,到达离他比较远的车站,也可以选择骑马或者步行,直接到达他想去的那个较远的车站。我们知道,如果直接去较近的车站,显然路程会近一些。但是,如果这么走的话,虽然路程走得少,但因为速度慢,花费的时间却更长一些。
再来举一个例子。如图所示,一个通讯员要从A地到C地去送一份文件,他是骑马去的。从A地到C地,中间要经过一大片沙地和另一大片草地,沙地与草地的分界线是EF。我们知道,马在沙地里行走的时候速度会很慢,大约只有草地上速度的一半。那么,这个通讯员应该选择什么路线走,才能快一些把信送到C地呢?
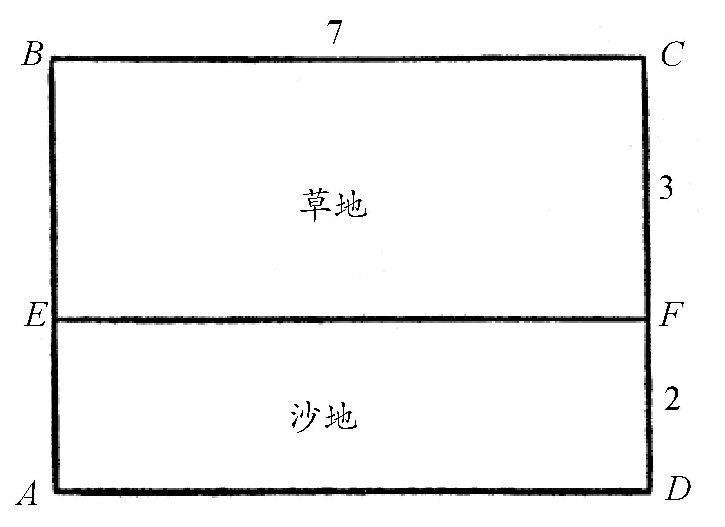
图 通讯员从A地到C地的最快路线。
不容置疑,从A地到C地,最近的路径是它们两者之间的连线,但这么走并不是最快的,这个通讯员不可能选择这条路线,因为他知道沙地上是很难行走的,所以他应该在沙地里少走一些路。也就是说,通讯员应选择在沙地里花费更少一些时间。虽然这么走可能需要在草地里走多一些路,但是从时间上来看,肯定要少得多,因为草地 上的行进速度是沙地的2倍。所以尽管在草地上多走一些,从花费的时间来看,还是有利的。也就是说,通讯员走的路线应该是这样的,尽量沿着A地到EF的垂线行走,然后到达分界线EF时,再折向C地。
通过几何学上的勾股定律,我们可以很容易地计算出,直线AC并不是花费时间最少的路线,如果按照 图 所示的路线AEC行进,其速度比直接沿着路线AC走快得多。
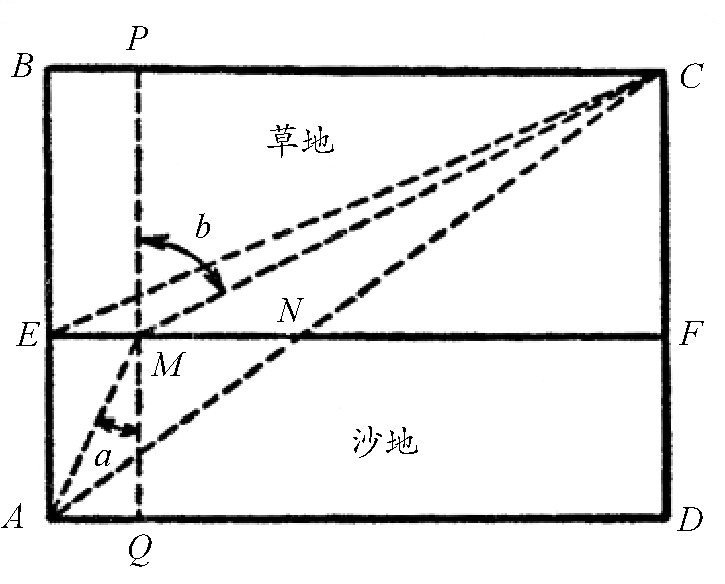
图 通讯员的最快路线是AMC。
下面,我们来计算一下图中的情况。在图中,沙地宽2千米,草地宽3千米,B到C的距离是7千米。那么根据勾股定理可以得出:
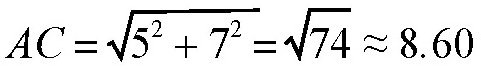
这里,AN部分代表在沙地里走的路线。可以看出,AN等于2/5的AC ,即 3.44 千米。由于在沙地里走的速度只有草地上速度的一半,所以这3.44千米所花的时间就等于在草地里走6.88千米花费的时间。所以,如果沿着路线AC走,走完全程就相当于在草地上走12.04千米所花的时间。
现在,我们再来看看图所示的情况,也就是沿着路线AEC行进。沙地里所走的路线AE长度是2千米,也就是相当于在草地上行走4千米,而路线EC长度是7.61千米,那么,两者相加,就相当于在草地上行走11.61千米。显然比图所示的情况花的时间要少多了。
这么说来,虽然路线AC看起来距离短,但花费的时间却相当于在草地上行走12.04千米,而路线AEC看起来距离长一些,但花费的时间却只相当于在草地上行走11.61千米。它们之间差了0.43千米。其实,图所示的情况还不是最快的。理论上来讲,最快的路线应该是这样的:角b的正弦值与角a的正弦值之比等于草地上速度和沙地上速度的比(sinb:sina),即2∶1。也就是说,要想花最少的时间,路径的选择必须满足sinb等于sina的两倍。通过计算,我们可以得出:

那么将全部的路程换算为在草地上行进的路程可知:
这就相当于在草地上行走4.47千米。
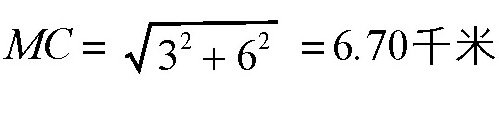
,全程为6.70+4.47=11.17千米。
由之前的计算,我们已经知道行走直线路程长度的时间相当于在草地上行走12.04千米的时间。
从刚才的例子可以看出,如果选择恰当的行进路线,花费的时间要少多了。光在不同的介质中传播时,就是这么选择的。如 图 所示,折射角的正弦值和入射角正弦值的比值,正好等于光在两种不同的介质中传播的速度的比值。通常我们把这个比值称为“折射率”。

图 线段m与圆的半径比是角1的正弦。线段n与圆的半径比是角2的正弦。
费马原理把光的反射和折射放到一起进行讨论,得出了“最快到达原理”,即不论在什么介质中传播,光走过的路径都是耗时最短的。
还有另外一种情况,就是介质是不均匀的。换句话说,这种介质的折射率是不固定的。比如,我们生活的大气层就是这样的情况。但是,在这种情况下,光依然选择最快的路径进行传播。这样就解释了光在进入大气层的时候,光的传播是慢慢变化的。天文学家把这一现象称为“大气现象”。因为大气层的密度从上到下是逐渐变大的。在这样的大气层里,光传播的路径是慢慢折向地面而不是一条直线的。这时,光线在大气层的上层传播的时候,传播的速度比较快,而且传播的时间也会长一些,而在大气层的下层,速度则比较慢,走的时间也短一些,这样光就会更快到达地球。
其实,前面提到的费马原理并不只适用于光的传播。对于声音的传播,不论是哪一种波动,也一样适用。
提到声音的传播,那么声音的波动特性到底是什么样的呢?1933年,在斯德哥尔摩的诺贝尔奖颁奖仪式上,现代物理学家、诺贝尔物理学奖得主薛定谔做了一个报告,对这一特性进行了解释。
还是以前面士兵行进为例,只不过这里我们假设地面情况是不均匀的。下面我们就来看一下,他当时是怎么解释的。他是这样说的:
假设每一个士兵手里都拿着一根长杆,这样可以使整个队伍始终保持整齐。假设地面是逐渐变化的,这时,上级命令所有的士兵以最快的速度跑步前进,一开始整排士兵的右侧走得比较快,左侧是后面才跟上去的。也就是说,整排士兵在进入不同的路况时,要想队伍保持整齐,需要有一定的时间,而且走的路线也不是直线,而是变得曲折了。但是,可以肯定的是,他们到达目的地的时间是最快的,因为他们的速度是最快的。
