相信读者们一定听说过“方圆问题”,就是已知一个圆的面积,要求做一个正方形,面积和这个圆的面积相等。这是几何学上的一个著名的题目。在2000年前,数学家们就开始研究它。我确信,在读者朋友中间,肯定有人也曾经试图解答它。但是,对于很多读者来说,对于这个问题的不可解可能没有深入研究,对它困难的理解也是千奇百怪。很多人可能会随着别人说,方圆问题不可解,但是,对这个问题的实质和解答上的困难之处,却并不清楚。
在数学上,不管从理论上说,还是在实际应用中,有很多题目都要比方圆问题有趣得多。但是,没有一个题目会像方圆问题一样,被大家所熟知。关于方圆问题,已经是老生常谈的题目了。2000年来,很多杰出的数学家和数学爱好者,为解答它付出了巨大的努力。

其实,在实际应用中,经常会碰到这个题目。在实际生活中,通常以一个近似值作为解答。但是,这个有趣的古老问题,却要求人们非常精确地画出这个等面积的正方形。作图的条件只有两个:
●已知圆心的位置和半径,画出这个圆。
●已知两个点,通过它们作一条直线。
题目要求只使用两种绘图工具来作图,一个是圆规,一个是直尺。
在非数学界人士中,流传着这样一种看法:他们认为,这个题目的困难就在于圆周和直径的比,也就是π值,不可能用一个精确的数值来表示。其实,这只是狭义上的理解,这是由π的本质决定的。实际上,如果把一个矩形变成一个等面积的正方形,这是很容易的,而且可以完成得非常精确。那么,要把一个圆变成一个等面积的正方形,就相当于只用直尺和圆规作一个等面积的矩形。我们知道,圆的面积公式是:
S=πr2或者S=πr×r
从这里可以看出,圆的面积就等于一个边长是r的正方形面积的π倍。所以,问题就演变为作出一条某个长度的π倍的线段。我们知道,π的精确值并不是3
,也不是3.14或者3.14159。π的值是一个位数无止境的数字。
这就是π的特性,它是一个无理数。在18世纪的时候,数学家朗伯特和勒尔德尔指出了它的这一特性。但是,π是无理数这一点并没有使那些狂热求解这一问题的人中断努力。在他们的理解中,即便π是无理数,并不代表这个问题是不可解决的。实际上,确实有一些无理数是可以用几何学的方法把它们的图作出来的。比如,要求作一段某个长度的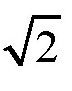
倍的线段。我们知道,
也是一个无理数。其实,这个问题很容易解决。只要作出一个正方形,使它的边长等于这个长度,那它的对角线长度就是要求的线段。
如果要作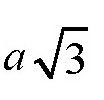
的线段,即便是初中生,也很容易找到答案,这其实是一个圆的内接等边三角形的边长。不仅如此,下面的这个无理数,也可以用图的方法作出来:

要想求出这个式子的值,只要作出一个正六十四边形就可以了。
由此可见,一个无理数,并非完全不可能用圆规和直尺作出它的图来。所以,方圆问题不可解,并不仅仅是因为π是一个无理数,而是因为π的另一个特性。π其实并不是一个代数学上的数,所以它不可能是一个有理数方程的根。我们把这种数称为超越数。
14世纪的时候,法国有一位数学家叫维耶特,他证明了下面的式子:

如果这个式子中的数是有限次的运算,那么就可以解决方圆问题了,我们就可以用几何学的方法把这个式子作出图来。但是,上式中的分母是无穷的,所以这个公式对于解决方圆问题并不能带来帮助。
也就是说,方圆问题之所以不可解,是因为π是一个超越数,它不可能由一个有理系数的代数方程解出来。在1889年,德国有一位数学家叫林特曼,他严格证明了π的这一特性。所以,从某种意义上说,他也是唯一成功解答方圆问题的人,虽然这个答案是否定的,但是,他证明了,在几何学上,方圆问题是不可能作出图来的。于是,1889年以后,很多数学家都放弃了这一努力,方圆问题也告一段落。可惜的是,仍然有很多数学爱好者并不了解这一历史,所以他们一直在做着没有结果的努力。
这就是关于方圆问题的理论。
实际上,这个问题并不需要非常精确的解答。对于我们的日常生活来说,只有对这个问题有一个近似的求解方法,就足够了。
事实上,要作一个和圆的面积相等的正方形,只要取π的前七八位数就可以满足我们生活中的需要了,再多了也没有什么用。比如,取π=3.1415926就足够了。一般长度的测量,不可能得到七八位数的结果,更不用说更多位数了。如果采用8位以上的π值,是没有什么实际意义的,最后得到的精确度也不可能因此而更好。如果我们用7位数来表示半径,那么即便你用一个100位的π来计算,最终得到的圆周长的精确值也不会多于7位。以前,有些数学家花了很多精力取尽可能多的π的位数,实际上没有任何价值。而且,这种事情对于科学发展起的作用也非常微小,只是需要一些耐心而已。如果读者朋友感兴趣,也有足够时间的话,可以试一下。比如,利用下面的莱布尼兹无穷级数,计算出π值的上千位数字:

这里的计算必须非常小心,即便在上式中取2000000项,最终得出的π值也就是6位数。所以,这个练习题对于任何人来说都没有什么用处,更不可能有助于几何学题目的解答。
法国的天文学家阿拉戈对这一问题也有研究,他曾说过:那些想解答方圆问题的人,仍然在继续解答这个题目。其实,这个题目的不可解,早就已经被人们证明了。而且即便这个题目是可解的,对于我们的实际生活也没有什么意义。那些自以为聪明的人、专心求解的人,是不可能得到结果的。
最后,他还在文章中对这一现象进行了讽刺:
在所有国家的科学院,一直在跟那些想要求解方圆问题的人作斗争,结果发现,这已经成了一种季节病,在春天的时候会爆发。
