碰撞力学,钢球碰撞后的速度

通过对物体碰撞的学习，我们可以事先知道两个相互碰撞的物体在碰撞以后的速度是多大。不过，碰撞后的速度还跟相互碰撞的物体是否有弹性有一定的关系。

如果两个相互碰撞的物体没有弹性，那么这两个物体碰撞后得到的速度将是相同的。可以通过相互碰撞物体的质量和原来的速度，运用混合法求出碰撞以后的速度。

以购买两种不同价格的咖啡为例。有两种咖啡，一种的价格是8元/千克，一种是10元/千克，我们分别取3千克和2千克进行混合，那么混合之后的咖啡的价格就是：

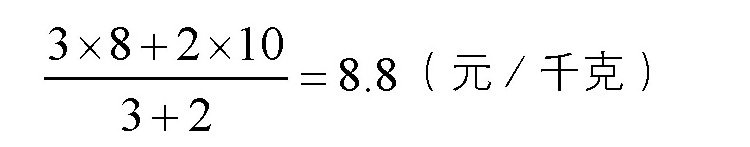
同样的道理，如果两个没有弹性的物体原来的速度分别是8厘米/秒和10厘米/秒，那么3千克的前者和2千克的后者相互碰撞，碰撞以后的速度将变成：

通常来说，如果两个没有弹性的物体的质量分别为m₁和m₂，速度分别为v₁和v₂，那么当它们相互碰撞之后，速度就是：

如果我们把速度v₁的方向看作正方向，那么，碰撞以后的速度u的方向就是这样的：

●计算结果为正数，说明u的方向与v₁的方向相同，也是正方向。

●计算结果为负数，则正好相反。

●对于没有弹性的物体之间的碰撞，只要了解这些就

可以了。

如果是弹性物体之间的碰撞，分析起来会复杂一些。跟没有弹性的物体不一样，当弹性物体碰撞的时候，首先会在碰撞的部位发生凹陷，然后又凸起来，最后恢复成原来的形状。所以，整个过程分好几个阶段。当物体凸起来的时候，撞过来的物体除了损失掉一部分在凹陷阶段的速度外，凸起来时也会失去同样的速度。而对于被撞的物体来说，它增加的速度也是双份的。也就是说，速度较快的物体会失去两份速度，而速度较慢的物体则增加两份速度。对于弹性物体之间的碰撞，记住这些就可以了，剩下的就是简单的数学计算了。假设速度较快的物体的速度为v₁，另一个物体的速度为v₂，它们的质量分别为m₁和m₂。由于两个非弹性的物体在碰撞以后将会以下面的速度运动：

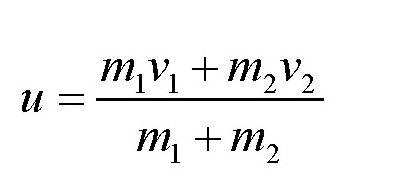
对于第一个物体来说，它失去的速度是₁vu；对于第二个物体来说，它增加的速度是₂uv。在前面分析弹性物体时，我们知道，失去的速度和增加的速度都是双份的，也就是2(v₁u)和2(u₂v)，所以两个弹性物体在碰撞以后的速度就是：

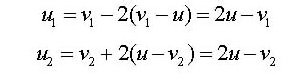
只要把前面的u值代入这两个式子，就可以得出两个速度值。

到此为止，我们对碰撞的两个极端情况进行了研究，即完全非弹性物体之间的碰撞和完全弹性物体之间的碰撞。但是，在实际生活中，更常见的是它们的中间情况，就是两个相互碰撞的物体并不是非弹性的，也不是完全弹性的。换句话说，在碰撞的第一个阶段之后，它们并不会完全恢复原来的形状。这种情况应该如何求解呢？后面，我们会讨论这个问题，在这里我们只需要知道这两个极端情况就可以了。

说到弹性物体的碰撞，我们还可以通过一个简短的规则来理解：弹性物体在相互碰撞以后，会以碰撞前相接近的速度远离。其实，只要简单地思考一下，我们就可以得到这个规则：

●弹性物体在碰撞前相接近的速度为v₁v₂。

●弹性物体在碰撞后相远离的速度为u₁u₂。

把前面的u₁和u₂代入上面的两个式子，可得：

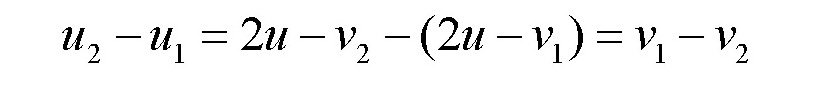
这是一个非常重要的性质，可以让我们对弹性物体之间的碰撞有一个清晰的印象。而且，它还包含着另一层意思。在前面推导公式的时候，我们提到过“撞过去的物体”和“被撞的物体”，这里的描述是针对未参与其中的旁观者来说的。在的开篇有一个关于两只鸡蛋的题目，“撞过去的物体和被撞的物体”与两个鸡蛋的情形是一样的。这两个物体的角色可以互换，对整个现象的本质没有任何影响。对于这一点，在本节中也适用吗？如果我们把这两个角色进行一下互换，前面推导出的公式会不会有什么变化呢？

可以看出，变换角色对上面的公式不会有任何变化。这是因为，无论从哪个角度来看，两个物体在碰撞之前的速度差都是相等的，所以两个物体在碰撞以后离去的速度也不会有任何变化，仍然是u₂-u₁=v₁-v₂。也就是说，无论从哪个角度看，两个物体相互碰撞以后的情形都是一样的。

最后，我们来看一些弹性小球在碰撞过程中的很有意思的数据。两个钢球的直径相同，都是7.5厘米，它们都以1米/秒的速度向对方撞去，产生了1500千克的压力。如果速度变为2米/秒，压力也会变大，变成3500千克。当两个钢球以不同的速度相互碰撞的时候，接触部分的半径也不同，分别是1.2毫米和1.6毫米，不过碰撞所持续的时间却是一样的，差不多都是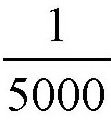

秒。这个时间是非常短的，所以在这么大的压力下，钢球并不会被撞坏。

需要说明的是，对于这两个小球来说，它们的碰撞时间非常短，这个结论是科学的。通过计算，可以得出：如果钢球非常大，像行星那样大，半径达到上万千米，再以1米/秒的速度相互碰撞，那么它们碰撞所持续的时间将会是40个小时，它们相互接触部分的半径将是12.5千米，它们之间的压力将达到惊人的4万万吨。