【题目】如图所示,上面画着8个大小相等的圆,其中有7个画着黑色线,它们都固定不动。第八个则紧贴着这7个固定的圆滚动。那么,当这个圆绕其他7个固定的圆一周时,它自己转了多少圈?
关于这个题目,我们可以用实验的方法找到答案:找8个同分值的硬币,按照图中的样子摆好,把7个硬币固定在桌面上,然后拿着另一个硬币绕着它们一路转下去。为了准确记住这个硬币转的圈数,必须仔细注视硬币上数字在什么位置。当硬币上的数字转到原来的位置,就代表它转了一周。
只要把这个实验真正地做出来,而不是靠想象,我们就会得到这样的结论:硬币一共转了4圈。
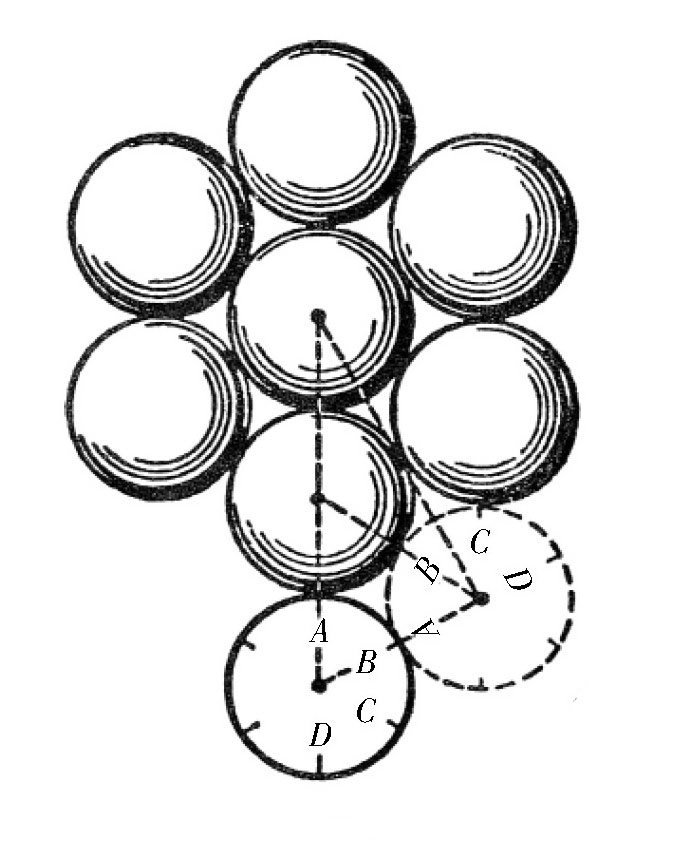
图 一个圆绕7个圆。
现在,不用这个方法,只用思考和计算,我们也可以得出同样的结论。
下面,我们就来分析一下,这个旋转的圆在每一个固定不动的圆上走的弧线究竟有多长。为了实现这个目的,我们假设活动的圆是从顶点A向邻近的两个固定圆之间的凹地移动,如图中的虚线所示。
从图中可以看出,圆滚动形成的弧线AB包含60°的角。而在每一个固定的圆上,都有两条这样的弧线,如果把它们加在一起,就是120°的弧线,或者说,它们是圆周的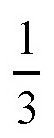
。所以,滚动的圆在围绕每个固定的圆转圈的时候,自己也转了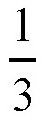
圈。这些固定的圆一共有6个,这样的话,活动的圆一共转了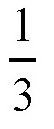
6=2圈。
很明显,这个答案跟实验的结果并不一样,但是,我们只相信事实。如果计算得到的答案跟事实不一致,肯定是计算出现了错误。那么,错误出在哪儿了呢?
【解答】错误就在于:如果我们把活动的圆沿着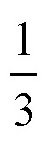
圆周长的直线滚动,这个活动的圆确实转了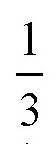
转。但是,如果这个活动的圆是沿着一种曲线形的弧线滚动,那么刚才的说法就不正确了,在这个题目中,如果活动的圆围绕相当于圆周长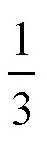
的弧线旋转,那它转的就不是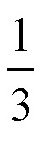
圈,而是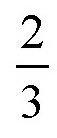
圈了,所以当这个圆围绕这6个弧线转完的时候,就是转了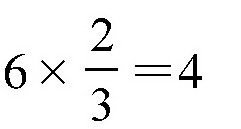
圈!
关于这一点,我们可以从下面的文字得到证实。
图中的虚线表示,活动的圆围绕固定的圆上的弧线AB(60°)转动,就相当于整个圆周长度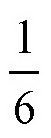
弧线时的位置。这个圆到了新位置时,最高点就不是点A了,而是点C,从这里可以看出,这就相当于圆周上的各点移动了120°,或者说,移动了整个圆周的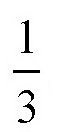
。对于活动的圆来说,固定的圆上120°的长度就是整个圆周的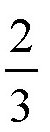
。所以,如果活动的圆沿着某条曲线(或者折线)转动,那么它转出的圈数跟沿着同样长度的直线转出的圈数是不同的。
我们不妨多花一些时间在这个问题上。关于解答这个问题的几何学原理,经常使我们难以相信。
假设有一个圆,半径是r。沿着一段直线向前滚动。如果直线的长度正好是它圆周的长度,它会转一圈。现在,如果我们在这条直线的中间处把它弯折,如图所示,并使CB跟它原来的方向成α角。那么,这个圆在转了半圈之后,就会到达点C了,为了转到直线CB上去,这个圆连同圆心就要转一个角度,也是α。
由于圆在转弯的时候并没有沿着直线移动,产生了比沿着直线滚动多出来的旋转。这个多出来的旋转跟整个圆周旋转间的比,正好跟α和2π的比相等,也是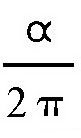
。然后,这个圆又在直线CB上滚了半圈,所以这个圆在整段折线ACB上,总共滚转了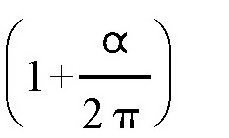
圈。
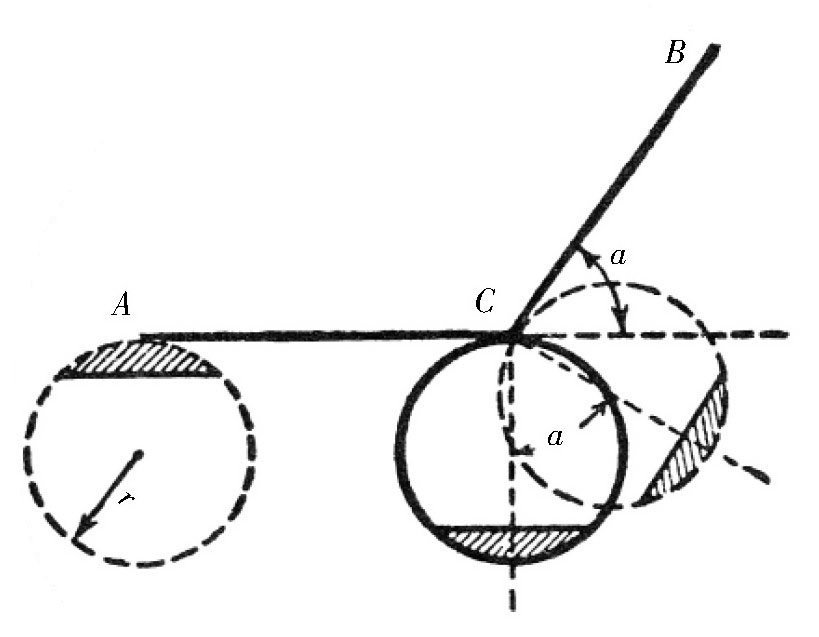
图 圆形在折线上滚动,多出来的旋转是这样产生的。
如果认识到这一点,我们就不难得出图的答案了。这是一个活动的圆绕着一个正六边形旋转,那么它一共转了多少圈呢?很显然,它转动的圈数应该等于这个圆在每个边的直线上转的圈数的6倍,然后再加上6个外角的和除以2π。我们知道,任何一个凸角多边形的外角和恒等于2π,所以得到,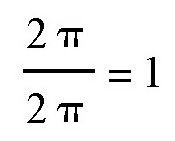
。
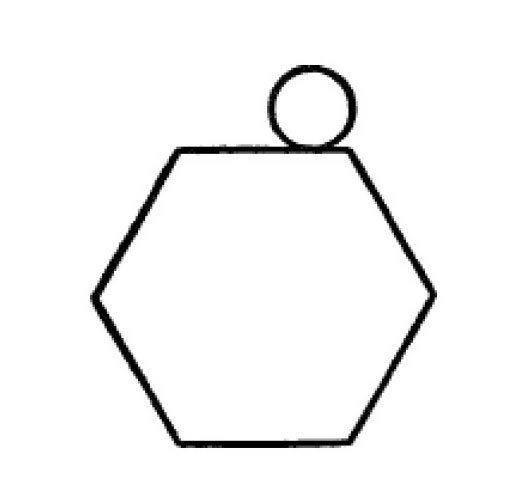
图 圆形在多边形的外边滚动,比它在与多边形同长等长的直线上滚动时,多滚动了几圈。
也就是说,这个圆在六边形或任何一个其他的多边形的外边旋转滚动时,如果它滚动了一周,那么它自己转动的圈数比它沿着这个多边形各边总长度相等的直线上滚动转动的圈数正好多1转。
一个凸角的正多边形,如果它的边数无穷增加,就会慢慢接近一个圆,所以刚才得到的结论,也适用于圆。比如,如果把一个圆放在另一个同样大小的圆外面沿120°的弧线滚动,那么这个活动的圆就转动了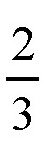
圈,而不是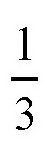
圈。这一点是有几何学依据的。
