三次不定方程的解

对于整数3，4，5，6，有下面的关系：

3³+4³+5³=6³

这个等式可以理解为，边长分别为3，4，5的3个正方体的体积之和等于边长为6的正方体体积，如图所示。据说，柏拉图对满足这一关系的数字曾进行过研究。

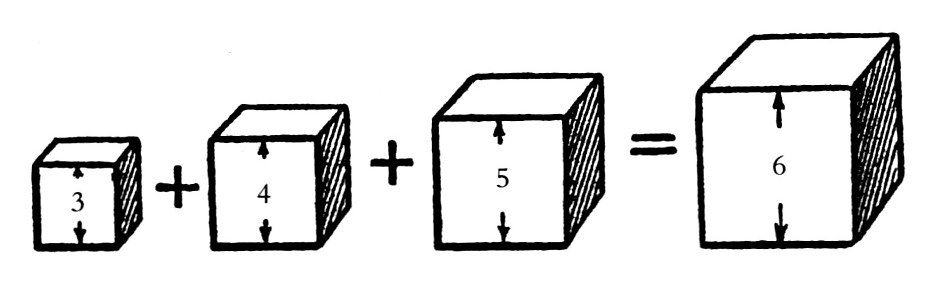
我们也来讨论一下这一问题，看能否找出别的这一类等式。即求解下面的方程：

x³+y³+z³=u³

为便于分析，假设这里的u=t，则方程变为

x³+y³+z³+t³=0

下面来看如何求解这个方程的整数解。假设a，b，c，d和α，β，γ，δ是满足方程的两组解。将后一组解同乘以k，并跟前一组解对应相加，选择恰当的k值，使得下面的这组解

a＋kα，b＋kβ，c＋kγ，d＋kδ

也满足上面的方程。也就是说，选择恰当的k值，使得

（a＋kα）³＋（b＋kβ）³＋（c＋kγ）³＋（d＋kδ）³＝0成立。

由于

a³+b³+c³+d³=0

α³＋β³＋γ³＋δ³＝0

所以，可以得出

3a²kα＋3ak²α²＋3b²kβ＋3bk²β²＋3c²kγ＋3ck²γ²＋3d²kδ＋3dk²δ²＝0

即

3k［（a²α＋b²β＋c²γ＋d²δ）＋k（aα²＋bβ²＋cγ²＋dδ²）］＝0

只要在两个乘数中有一个为0，上面等式就成立。首先，如果k=0，这时就相当于我们构造出的解：

a＋kα，b＋kβ，c+kγ，d＋kδ

仍然是a，b，c，d。这对于我们来说没有任何意义。

所以，考虑

（a²α＋b²β＋c²γ＋d²δ）＋k（aα²＋bβ²＋cγ²＋dδ²）＝0

得到

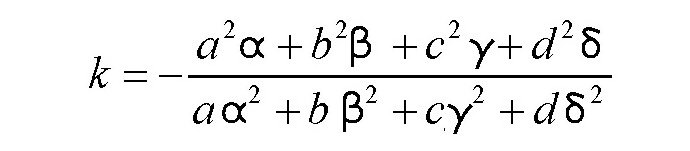
也就是说，如果已经知道了方程的两组解，只要在其中一组解的前面都乘以k，再加上另一组解的对应值，就可以得到第三组解，其中k的值用以上方法求出。

在本节一开始，我们已经知道了一组解3，4，5，－6，只要再找到另一组解就可以了。如何找到这样的一组解呢？其实很简单，可以取r，－r，s，－s。很明显，它们满足前面的方程。取

a＝3，b＝4，c＝5，d＝－6

α＝r，β＝－r，γ＝s，δ＝－s

容易得出此时的k值为：

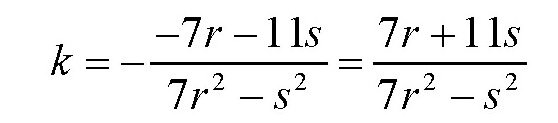
a＋kα，b＋kβ，c＋kγ，d＋kδ分别等于：

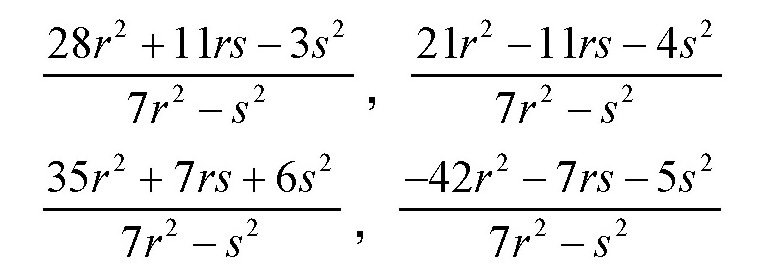
根据前面的分析，这4个值满足前面的方程

x³+y³+z³+t³=0

在以上4个数中，分母都是一样的，可以消掉。即下面的4个数也可以满足方程：

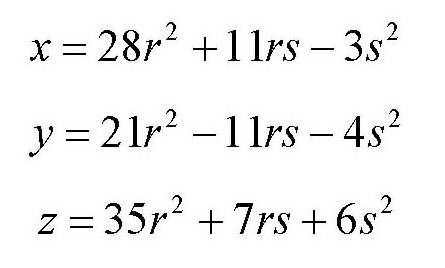
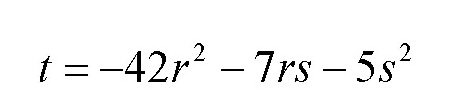
将r和s分别取不同的整数值，就可以得到满足方程的很多个解。如果这些解有公因数，可以把公因数约去。比如当r=s=1时，得出的解为36，6，48，－54，这时可以把公因数6约去，得出6，1，8，－9。所以

6³+1³+8³=9³

下面列出了方程的一些解：

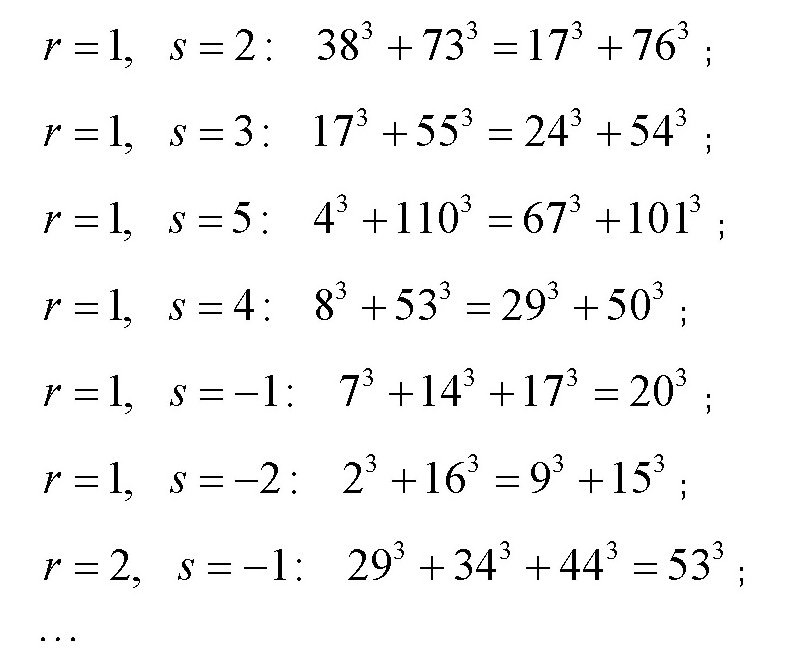
需要注意的是，如果把前面的一组解3，4，5，－6或者新得出的一组解中的数换一下顺序，就可以得到一组新的解。比如说，令

a＝3，b＝5，c＝4，d＝－6

可以得出

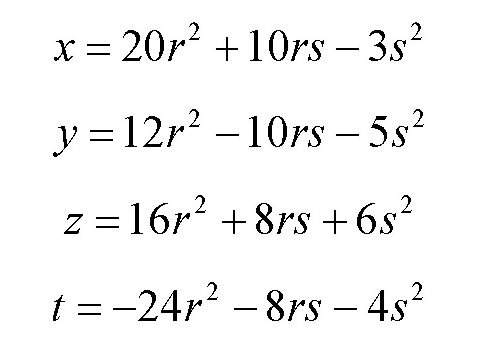
此时，对于不同的r和s，也可以得出方程的一些解

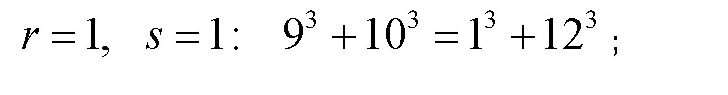
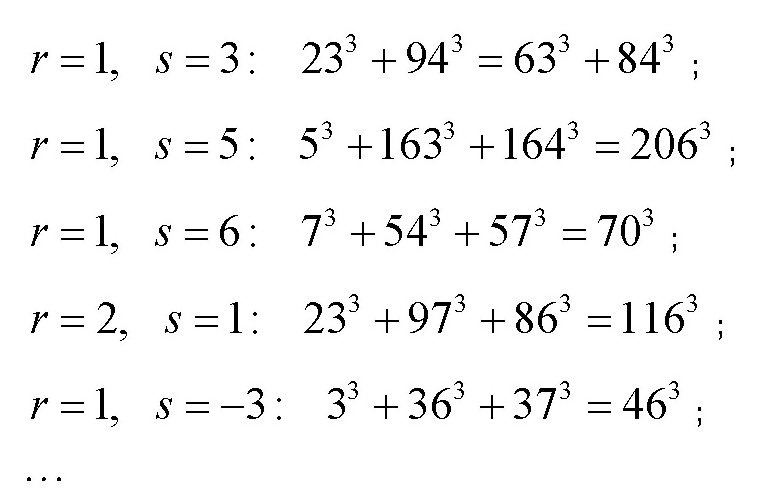
通过该方法，可以得出满足这个方程的无穷多个解。