如果你对力学没有进行过深入研究,可能会有这样一种感觉:如果力量比较小,是不可能移动质量非常大的自由物体的。其实,这也是犯了常识性错误。学习力学可以帮助我们解答这个疑问,它会告诉我们:再微小的力量,都可以使任何物体——不管这个物体的质量有多大——产生运动,只要这个物体是自由的物体就可以。前面我们已经用到下面这个公式很多次了。
F=ma
所以有:
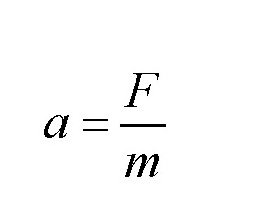
通过这个式子,我们可以得出,只要力F不等于0,加速度a就不等于0。也就是说,不管力F多么小,都会产生一个不等于0的加速度,自由物体就会产生运动。
遗憾的是,在我们所处的环境中,很难证明这个定律的正确性。这是因为,摩擦是无处不在的,总是存在着运动的阻力。我们很难找到自由物体的踪影。我们所见到的物体运动都是不自由的。所以,要想使物体产生运动,我们还需要克服摩擦阻力,这就要求我们加在物体上的力要比摩擦力大。比如,我们要把干燥橡木地板上的一个橡木柜子推离原来的位置,需要的力量大概是柜子重力的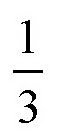
。这是因为,柜子与地板相互接触的面都是干燥的橡木,它们之间的摩擦力大概是物体重力的34%,移动柜子必须要克服这个阻力。如果它们之间不存在摩擦力,那么只需要一个非常小的力。比如,用手指轻轻碰一下,就可以推动这个柜子了。
在自然界中,不受到摩擦等介质阻力的物体非常少。一般来说,太阳、行星、月球,以及我们生活着的地球等一些天体都是自由物体,它们的运动是完全自由的。那是不是说:我们可以把地球推动呢?事实上也的确是这样的。我们可以这么认为:我们在运动的同时,带动了地球的运动。
再比如,当我们从地面上跳起来的时候,我们得到了一个速度,同时,地球也会朝着相反的方向运动。说到这里,有的读者可能会问这样一个问题:既然如此,那地球的运动速度会是多少呢?我们可以根据牛顿第三定律来进行计算。对于地球来说,我们给它的力量等于我们的身体跳起来时的力量。这两个力的冲量相等,我们和地球的动量也是相等的。假设地球的质量为M,地球的速度为V,我们人体的质量为m,我们跳起来的速度为v,则有下面的关系:
MV=mv
也就是:
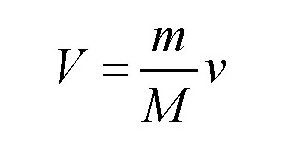
我们知道,人的质量跟地球比起来要小得多,所以地球的速度一定比我们跳起来的速度小得多。当然了,我们这里用“小得多”来进行描述,给读者的感觉一定很模糊。其实,对于地球来说,我们是可以得出它的质量的,所以可以计算出这个速度的近似值。
我们一般认为地球的质量是6×1027克。在这里,人体的质量m取60千克,也就是6×104克。两个质量的比值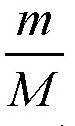
就是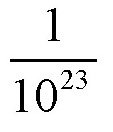
。换句话说,地球得到的速度只有人跳起来的速度的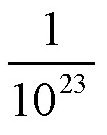
。假设我们跳起来的高度h为1米,那么可以利用下面的公式计算出我们的初速度:
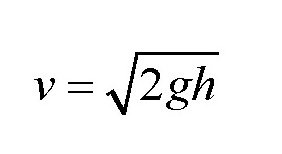
即:

所以,地球的速度为:

客观地说,这个数值非常小,小到我们想象不出它究竟是个什么概念,但是它毕竟不等于0。那么,这个数到底是多大呢?我们可以这么想象一下:如果地球一直保持这个速度运动下去,那么在接下来的非常长的一段时间里,比如,十万万年,地球会移动一定的距离,那这个距离是多大呢?我们可以根据下面的式子来计算:
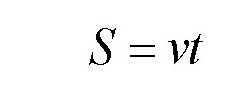
这里的时间t是十万万年,也就是:
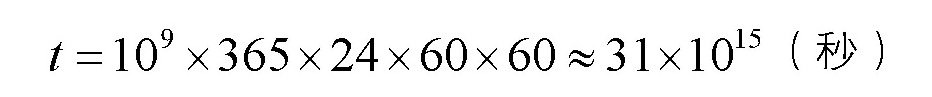
代入上式得:
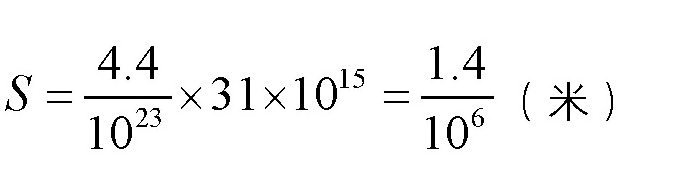
如果换算成微米,就是:
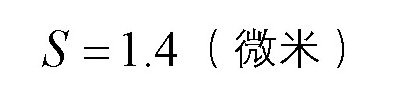
从这个结果可以看出,在十万万年这么长的时间里,如果地球一直按照刚才的速度运动下去,它也只不过运动了1.4微米的距离。我们根本无法用肉眼辨别出这个距离来。
事实上,对于地球来说,我们刚才计算出来的速度并不会保持下去,当我们的两只脚离开地球的时候,仍然会受到地球引力的作用。在地球引力的作用下,我们的运动速度会降低。而且,如果地球对我们的引力是60千克,那么我们对地球的引力也是这么大。所以,随着我们速度的降低,地球的速度也会降低,最终这两个速度都会降为0。
综上所述,我们确实可以给地球一个速度,但是这个速度维持的时间很短,而且又很小,所以并不能使地球移动起来。我们想让地球移动起来,必须满足下面的条件:如 图所示,找到一个和地球没有任何联系的支点。当然了,图中的景象只是一种幻想。不管你的想象力有多么丰富,无论如何你也想象不出我们的脚该放在哪里。

图 只要找到一个和地球没有任何联系的支点,人就可以让地球移动起来。
