如果读者朋友们学习过几何学知识,肯定会发现这样一个问题:在马因·里德的小说中,少年航海家在计算两个圆台的体积时,所采用的方法是不精确的。如图所示,如果我们用r表示圆台小底面的半径,用R表示大底面的半径,用h表示桶高,每个圆台的高度就是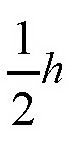
。少年用下面的式子计算容积:
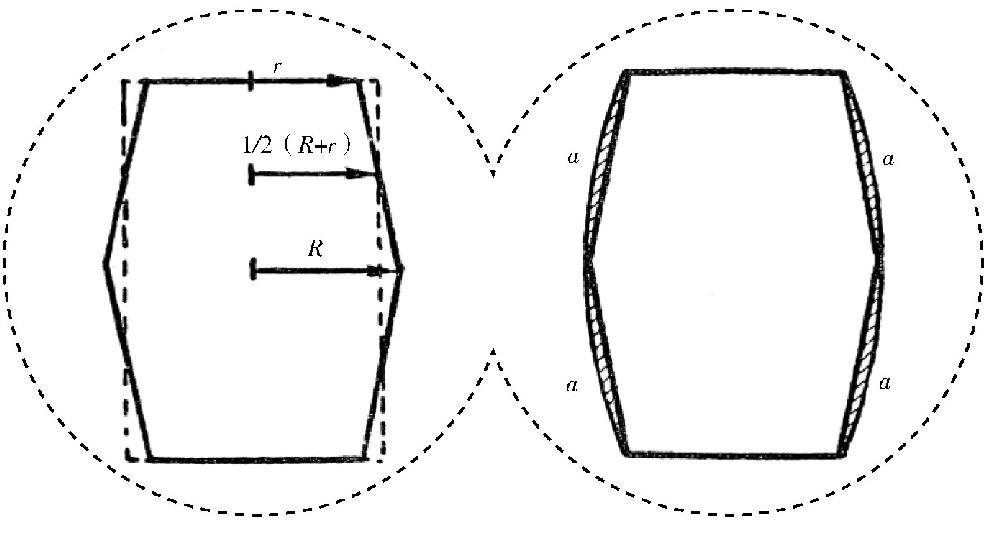
图 木桶体积的计算。
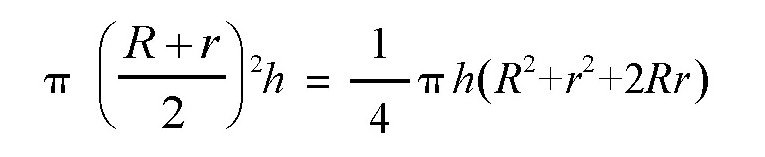
但是,根据几何学的知识,圆台的体积计算公式为:
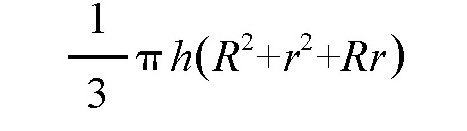
可以看出,这两个式子是不相等的,通过计算,我们可以得到,后者比前者要大一些,这个差值是:
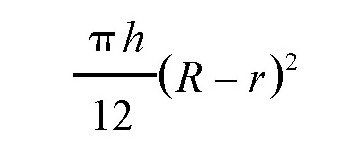
如果学习过代数学,我们就会知道,这个差值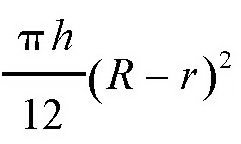
是一个正数,也就是说,少年航海家得出的结果比实际结果要小一些。
那么,究竟小多少呢?这可是个很有意思的问题。一般情况下,在制作的时候,水桶最粗的地方要比底面直径大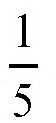
。也就是说,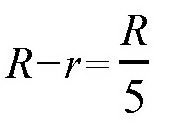
。假设小说中的那个水桶就是这样的,那么,我们可以求出两个圆台的体积跟实际体积的差值:
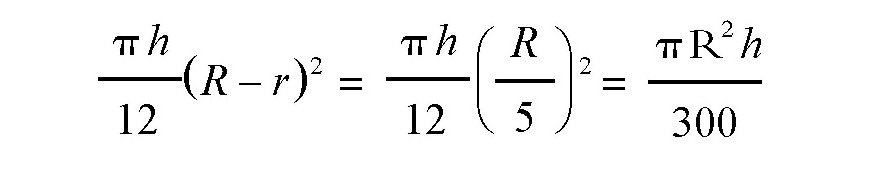
如果把π看作3的话,这个差值就是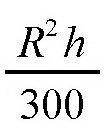
。也就是说,如果按照少年的计算方法,得到的体积跟实际体积的差值正好是以水桶的最大横截面作为底面、以水桶高度的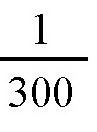
作为高的一个圆柱的体积。
其实,实际的差值比上面的结果还要大一些,这是因为水桶的容积比两个圆台体积的和要大。从图(右)可以看出,少年在计算的时候,并没有考虑图中阴影的部分,他把这部分忽略了。
前面关于水桶容积的计算方法,并不是马因·里德小说中描写的那位少年航海家自己想到的。在很多初等几何学书籍中,都利用这个方法来计算水桶容积的近似值。需要说明的是,要想精确计算出水桶的容积是很难的,对于这样的题目,在17世纪的时候,德国的天文学家开普勒也花了一番心血,试图求出它的精确值,在他留给后世的一些论文中,还有关于这个题目的专门讨论。但是,迄今为止,还没有找到可以求出精确值的简便方法。现在,人们只能通过实际经验,计算出一个近似值。比如,在法国南部,人们是用下面的公式来计算的:
水桶的容积=3.2hRr
实践证明,这个公式非常好用。
说到这里,还有一个问题,不知道读者朋友想到没有,就是:为什么要把水桶造成凸肚的形状呢?这样又不便于测量。为什么不把它造成标准的圆柱形状呢?其实,有很多桶的形状是圆柱形的,不过都是一些金属原料制成的,而不是木头制成的。那么,为什么要把木桶造成凸肚的形状呢?难道这种形状有什么优势?
是的,之所以把木桶造成凸肚的形状,就是因为这样可以很容易地把套到木桶上的桶箍套牢。在木桶的一头套上桶箍之后,用锤子把它向凸肚的地方敲下去,就可以把桶箍牢牢地套在木桶上,这样木桶就会非常坚固。
同样的道理,所有用木头制成的水桶、水盆等,都要造成这种圆台的形状,而不是圆柱形,如图所示,桶箍都是用同样的方法敲上去的,从而把水桶箍紧。
说到这里,我想顺便提一下开普勒关于这个题目的见解。在发现行星运动的第二定律(面积定律)和第三定律(周期定律)时,开普勒就注意到了木桶的形状问题,并进行了一些研究,他还以此为题,写了一篇论文,题目是《酒桶的立体几何学新论》。在论文的开头,他是这样写的:

图 桶箍可以把桶箍紧。
根据制造材料和使用需要,盛酒用的大桶有很多形状,有的是圆锥形,有的是圆柱形。如果把液体存放在金属制成的容器中,经常会因为锈蚀而腐败;而玻璃制成的容器或者陶器又不够大,也不够坚固,石头制成的器皿又太重,也不适合。所以,保存酒的办法只有一个,就是把它装在木头制成的容器中。如果把整个树干挖空,来制作木桶,这样制成的木桶不够大,而且也很难大量制造,即便造成了,也有可能破裂。所以,只能把一片片的木板拼凑起来,来制造这种木桶。最后,就是如何防止液体从缝隙间渗漏的问题了,即便用任何可能想到的材料填塞,都是不可能的,唯一的办法就是用桶箍把它们箍紧……
如果可以用木板制成一个球形的容器,那是最好不过了。但是,要想把木板箍成一个球形,这是不可能的,所以只好采用圆柱形了。而且,这个圆柱形还不能是十分标准的圆柱形,否则随着使用时间的延长,桶箍会变松,也就没有用了,没法继续箍紧那些木板了。所以,这个圆柱形必须是类似圆台的形状,木桶的中间要粗一些,这样,如果桶箍松动了,还可以继续向中间移动,箍紧木板。而且,这种形状便于搬运,汲取里面的液体也比较容易。另外,它的两边是对称的圆形,滚动起来也很容易,还非常美观。
这就是论文中的一段,读者朋友可不要以为这只是开普勒在随意调侃,这其实是一篇十分严肃的论文,其中,他引入了无穷小和微积分的原理,通过这个木桶,以及它体积的计算方法,把开普勒引向更深入的数学思维之中。
