有一种电子装置叫触发器,它主要由两个电子管组成,这种电子管跟收音机里的电子管差不多。通过触发器的电流必定会通过其中一个电子管,可能是左边的,也可能是右边的。在触发器里有两个接触点,用来接收外部的短暂电信号(脉冲);还有另外两个接触点,用来输出触发器的回答脉冲。在外面输入脉冲的瞬间,触发器就会转变状态,即进行“翻转”,这时,原来导通的电子管变成闭合状态,电流转而进入另一个电子管。当右边电子管闭合、左边电子管导通的时候,触发器就会瞬间输出回答脉冲。
现在,我们给触发器连续不断地输入几个电脉冲,看看它是怎样工作的。我们不妨根据右边的电子管来确定触发器所处的状态:当右边的电子管闭合,我们规定触发器处于“0状态”;当右边的电子管导通,我们规定它处于“1状态”。
假设触发器的初始状态是“0状态”,即左边的电子管导通,如图所示。输入第一个脉冲后,右边闭合的电子管变成导通状态,也就是触发器翻转成“1状态”。此时触发器不输出回答脉冲,因为只有右边的电子管处于导通状态时,才输出回答脉冲。
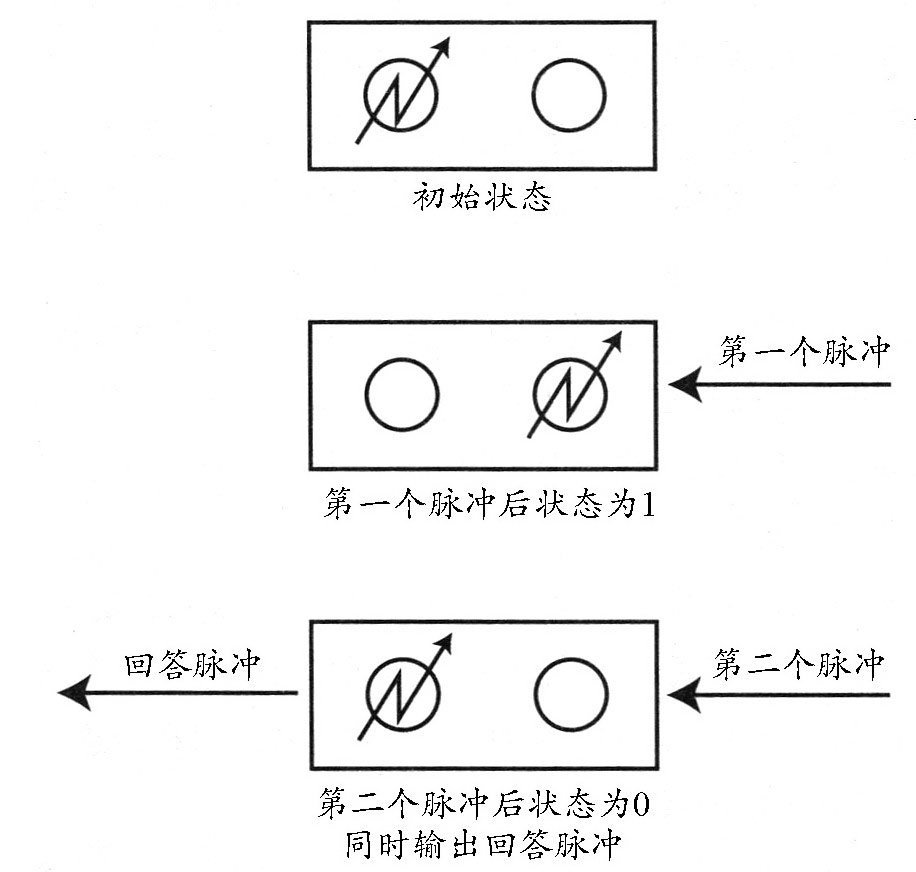
接着输入第二个脉冲,这时,左边的电子管变成导通状态,触发器又翻转到“0状态”,此时触发器输出回答脉冲。
在输入两个脉冲之后,触发器又回到了初始状态。所以,
继续输入第三个脉冲后,触发器处于“1状态”;输入第四个脉冲后,触发器又处于“0状态”,并输出回答脉冲,依次不停地循环下去。也就是说,每输入两个脉冲,触发器的状态就会重复一次。
假设现在有很多个这样的触发器,给第一个触发器输入脉冲信号后,把它输出的回答脉冲加到第二个触发器上,第二个触发器的回答脉冲再加到第三个触发器上,依次类推。如图所示,把它们顺次连接起来。现在,我们来看一下这些触发器会如何工作。

假设一共有5个触发器,它们的初始状态都是“0”。这样的话,我们就可以把它们的初始状态记为“00000”。输入第一个脉冲后,最右边的那个触发器就会转变成“1状态”,由于此时并没有输出回答脉冲,所以,后面的4个触发器仍然处于“0状态”,也就是说,现在的状态是“00001”。接着,我们输入第二个脉冲,这时,最右边的触发器就会翻转,变成“0状态”,并输出回答脉冲加到第二个触发器,使得第二个触发器发生翻转,变成“1状态”,而其他的触发器仍然处于“0状态”,所以,现在的状态变成了“00010”。接着,再输入第三个脉冲,这时,第一个触发器又会发生翻转,但不输出回答脉冲,所以其他的触发器状态都不会变化,这样的话,总体状态就是“00011”。接着,输入第四个脉冲,第一个触发器继续翻转,并输出回答脉冲,这个回答脉冲会使第二个触发器发生翻转,也输出回答脉冲,从第二个触发器输出的回答脉冲使得第三个触发器发生翻转,所以,这时的状态就变成了“00100”。
这样一直进行下去,我们就会得到下面的状态:
输入第1个脉冲后00001
输入第2个脉冲后00010
输入第3个脉冲后00011
输入第4个脉冲后00100
输入第5个脉冲后00101
输入第6个脉冲后00110
输入第7个脉冲后00111
输入第8个脉冲后01000
……
由此可见,这些连接起来的触发器,可以对外面输入的脉冲进行“计数”,并且是以一种特殊的“计数”方法来表示这些脉冲信号的。通过观察不难发现,这种“记录”脉冲信号次数的方法,就是二进制计数法。
在二进制中,用“0”和“1”表示所有的数。跟十进制不一样,二进制后面一位上的1是前面一位上的1的两倍,而不是10倍。二进制数转化成十进制数时,首先从右至左用二进制的每个数分别乘以2的相应次方数,即20,21,22,……然后再把所得的数相加即可。比如,二进制数“10011”转化为十进制数为1×20+1×21+0×22+0×23+0×24=19。
连接起来的触发器就是用这种方式对输入信号进行计数并记录的。需要注意的是,触发器每翻转一次,也就是每输入一个脉冲信号,大概只需要一亿分之几秒的时间。现代计数触发器在1秒钟的时间里,可以“计算”1000多万个脉冲。一般来说,即便你的眼睛可以辨别得非常快,也大概需要0.1秒才能识别出这个变换的信号,所以,跟人相比,它快了差不多100万倍。
假如把20个触发器按照以上的方式连接起来,也就是说,这一串触发器可以用20位的二进制来表示输入的脉冲信号,那么,它可以“计数”到220-1,这个数比100万还要大。而如果是64个触发器连在一起,则可以用它来“计数”著名的“象棋数字”(即264)了。
用触发器可以在1秒钟的时间里“计数”几百万个信号,这在核物理的研究中具有十分重要的意义。例如,原子在裂变时会释放出大量的粒子,这个数目非常大,就可以用这一方法来计数。
