上文就是凡尔纳所描述的“去地心旅行”的内容。如果我们用实验来检验一下对话所说的现象,你会发现事情并非如此。当然,我们并不需要真的下到地心里去,只需要准备一支铅笔和一张纸,就可以在物理学里做一次小小的旅行。
首先,我们来计算一下,下降到什么深度时,大气压才会增加千分之一。我们知道,一个正常的大气压的大小等于760毫米汞柱的重量。如果我们是在水银里,而不是在空气中,那么需要下降的幅度就是760÷1000=0.76毫米。这样的话,大气压力就可以增加千分之一。但是,我们是在空气中,所以肯定需要下降到更深的地方,这个下降深度应该是水银密度与空气密度的倍数之比,即10,500倍。因此,要想使大气压力增大千分之一,我们就需要下降0.76×10500,差不多是8米,而不是0.76毫米。我们再往下8米,大气压力就会继续增大千分之一。而且每往下一个8米,下一层的空气肯定要比上一层更密,大气压力增加的绝对值肯定也比上一层要大。所以,不管我们身在何地,是在数米的高空,还是在珠穆朗玛峰山顶(大约9千米高的地方),又或者是在海平面,要想使大气压比原始的大气压增加千分之一,都要下降8米。这样的话,我们就可以列出一个大气压变化的情况表:
在地面上,正常大气压为760毫米汞柱。
地下8米深处的空气压力=正常大气压的1.001倍。
地下2×8米深处的空气压力=正常大气压的(1.001)2倍。
地下3×8米深处的空气压力=正常大气压的(1.001)3倍。
地下4×8米深处的空气压力=正常大气压的(1.001)4倍。
总而言之,在n×8米深处的空气压力等于正常大气压的(1.001)n倍。根据马里奥特定律,当大气压力并不是特别大的时候,空气密度的增加倍数与大气压力是相同的。
我们可以看到,在小说中,旅行家到达的深度是48千米,所以可以不再考虑人体自身重力的减小和空气质量的减少。
现在,我们就来计算一下,小说中的旅行家们在地下48千米的地方,要经受的空气压力到底是多少。根据上面的公式可以算出此处n=48000÷8,也就是n=6000。由此可以计算得出大气压力为1.001的6000次方。如果这样不停地乘下去,就太费时费力了。这时候,我们可以利用对数来计算。就像拉普拉斯 所说的,对数可以大大减少我们的劳动量,所以计算者的寿命都可以增长了。
在学校里,有一些讨厌对数表的同学,如果你们读过拉普拉斯对对数的说明,说不定就会改变厌烦的态度。拉普拉斯在他的著作《宇宙体系论》中说道:
因为对数的发明,人们可以把本需要几个月的计算时间减少到几天。使用对数来计算,既可以提高正确率,还能够延长天文学家们的寿命。这是人类科学发展的宝贵财富。
在这里,我们通过使用对数,可以得到下面的算式:
6000× lg1.001=6000×0.00043=2.6
查表可知,2.6对应的对数是400。也就是说,大气压在48千米深处时是正常气压的400倍。通过实验可以证明,在这样的压力之下,空气密度也会增加315倍。所以,小说中的这两位地下游客竟然只是“耳朵有点儿疼”而已,而没有其他难受的症状,其可信度就实在不高了。不止如此,小说里甚至写了人们还到过地下120千米,甚至325千米这样深的地方。在这样的深处时,大气压力必然是一个非常大的数值,而人所能承受的大气压力是非常有限的,不能超过3个~4个大气压。
我们可以利用这个公式,计算出当大气密度增加770倍,达到水的密度时,要到一个什么样的深度。通过计算,可以得出深度是53千米。但这个计算结果是错误的,因为当气压已经非常大的时候,气体密度与大气压力就不是成正比的关系了。压力只有在不超过几百个大气压的时候,马里奥特定律才适用。下面所列的是通过实验得到的空气密度数据:

由左表可以看出,与气压的增加相比,气体密度的增幅更慢。所以,小说中的科学家凭空想象,认为在到达一定深度之后,空气密度会变得比水还要大是不可能的。因为只有在3000个大气压力的时候,空气才能够达到水的密度。在此之后,空气就基本不会再压缩了。空气要想变成固体,不仅需要满足压力的条件,还要在同时把温度剧烈降低,差不多要达到零下146℃才行。
不过,为了公平起见,这里要替小说家说句话,就是刚才所举的数据是在凡尔纳的小说发表后很久才被人们发现的。所以,我们应该原谅小说家所犯的物理学错误。
我们还可以利用上面的公式来计算一下:要想保证矿井工人的身体健康,他们所能达到的最大深度是多少。我们的身体所能承受的最大空气压力是3个大气压。对于需要计算的矿井深度我们用x来表示,那么可得:
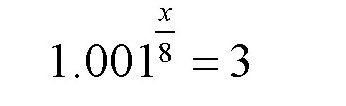
利用对数,我们可以得到x是8.9千米。
由此可知,在地下大约9千米的地方,人类都可以生存。假如有一天太平洋突然干涸了,人类基本上可以居住在海底的任何一个地方。
