凡尔纳笔下有一个叫马迪夫的大力士,“他的头很大,身子很高,胸膛壮得像铁匠的风囊,腿粗得像木头柱子,胳膊像起重机,拳头大得像铁锤……”大家知道他吗?他在小说《桑道夫伯爵》中曾立下汗马功劳,其中最引人注目的功劳就是徒手拉住了正要下水的“特拉波克罗”号大船。
凡尔纳是这样描写大力士马迪夫的这一壮举的:
支撑船身的物体已经移走,船已经做好了下水的准备。只要解开缆索,船就会离开岸边,顺着水滑下去。有五六个木工已经在船的龙骨下紧张地忙碌着,观众们则好奇地看着他们工作。就在这时,有一艘快艇进入了人们的视线,它绕过岸边凸起的地方急速行驶着。快艇如果想要进入港口,就必须从“特拉波克罗”号要下水的船坞前开过去。所以,船工为了避免发生意外,一听见快艇的信号,就赶紧停止了解缆工作,想让快艇先开过去。要知道,“特拉波克罗”号是横着驶入大海的,而快艇正以极快的速度冲过来,如果快艇撞到了大船,一定会沉没的。
夕阳下,“特拉波克罗”号白色的篷帆就像是镀了一层金漆,非常华丽,所有的人都注视着它。此时,工人们已经停止了手头的工作。快艇的速度很快,已经出现在船坞的正前方。此时,船坞上无数的观众都目不转睛地盯着它,想看它能否安全地冲过去。突然,人群中传来了一阵惊呼,原来在快艇的右舷正对着“特拉波克罗”号大船的时候,大船竟然摇摇摆摆地滑下去了,而且正以很快的速度斜着向下滑去。此时,大船的船尾已经入水了,船头也升起了因摩擦而产生的烟雾……眼见这两条船就要撞上了——一场可怕的灾难似乎已无法避免!
这时候,突然有一个人出现了!他用手抓住了 “特拉波克罗”号船身上的缆索,身子几乎贴在了地面上。他铆足了劲儿,拉着大船,只用了1分钟,就把船拉了回来,把缆索固定在了地上的铁桩上。这时候,他依然冒着被摔死的危险,一直用手紧紧地拉着缆索,坚持了十几秒钟。最后,缆索断了。但就在这宝贵的十几秒的时间里,快艇迅速开了过去,只是与“特拉波克罗”号轻轻地擦了一下。缆索断了,大船也迅速地向前驶去。
就这样,在大力士的帮助下,快艇得救了。而这位挽救灾祸的英雄,就是马迪夫。他的行为是如此迅速,以至于当时没有一个人来得及帮他一把。
假如有人对凡尔纳说:“当时那种情况下,避免两船相撞的灾难,可能并不需要大力士,也不需要大力士那样超级大的力量。其实,一个身手敏捷的人就能够完成同样的事情!”小说作者肯定会十分惊讶的。
根据力学原理,绳索在桩上滑动的时候,其产生的摩擦力可以达到最大,而且绳索缠绕在桩上的圈数越多,摩擦力越大。当圈数按照算术级数增加的时候,摩擦力就会按照几何级数递增,这就是摩擦力递增的规律。所以,就算是一个小孩子抓着绳头,只要能把这条绳索在一个固定的桩上绕个三四圈,都可以平衡一个相当大的重物。
一些在轮船码头上工作的船工,拉着载有几百个乘客的轮船靠岸,利用的就是这个原理。拉动大船靠岸的可不是这些工人的臂力,而是绳子与桩子之间产生的巨大摩擦力。
18世纪著名的数学家 欧拉 已经算出了摩擦力大小跟绳索缠绕木桩圈数之间的关系:
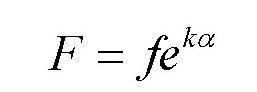
其中,f表示我们所用的力;F表示f的阻力;e为2.718……(以自然对数为底);k表示绳子和桩之间的摩擦系数;α表示绳索所绕的长度与弧的半径之间的比值,也被称为绕转角。
下面,我们将小说中的情节套用到这个公式中计算一下,你会发现结果非常令人吃惊。小说中说船重50吨,假设船坞的坡度是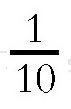
,那么就不是整个船的重量都作用在缆索上,而只是它重量的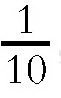
,也就是5吨或者5000千克作用在绳索上。力F是沿着船坞向下滑的船对缆索的拉力。我们将缆索和铁桩的摩擦系数k定为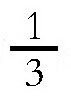
。小说中,马迪夫将缆索在铁桩上绕了3圈,此时α的值也可以算出来了:
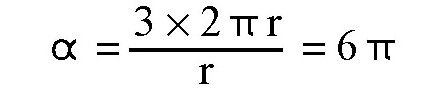
我们将这些数值代入欧拉公式,得到:
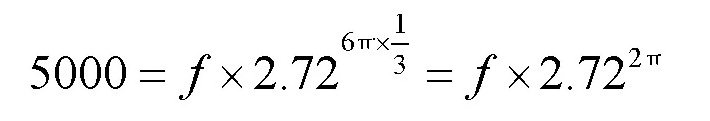
我们需要的人力f就可以用对数计算出来了:
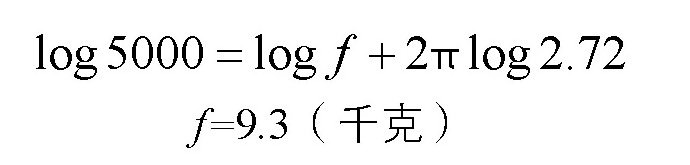
实际上,这个大力士只需要用不到10千克的力气,就能够把缆索拉住!
可能有人会觉得:10千克只是理论上的数据,真去拉的话肯定不止需要这么小的力气。实际情况恰恰相反,10千克的结果已经相对较大了。古代,人们是用麻绳和木桩系船的。这两样东西间的摩擦系数k可比上面的数值大多了,所以实际需要的力气会更小,甚至小得让人难以想象。所以即使是没什么力气的小孩子,只要绳索足够结实、牢固,能够承受得住拉力,在将绳索绕上木桩三四圈之后,也能把船拉住,立下大力士的功劳,甚至还可能胜过他。
