整数勾股弦数的特性

土地测量者经常使用一种非常简单又准确的方法画垂线，步骤如下：如图所示，假设要过点A作垂直于MN的线。a是任意长度，先沿着AM方向取a的3倍，再找一根绳子，在上面打三个结，使结与结之间的长度分别是4a和5a，然后把两端的结分别固定在点A和点B上，拉直绳子，另一个结所在的地方就是点C。这样就形成了直角三角形ABC，其中角A为直角。

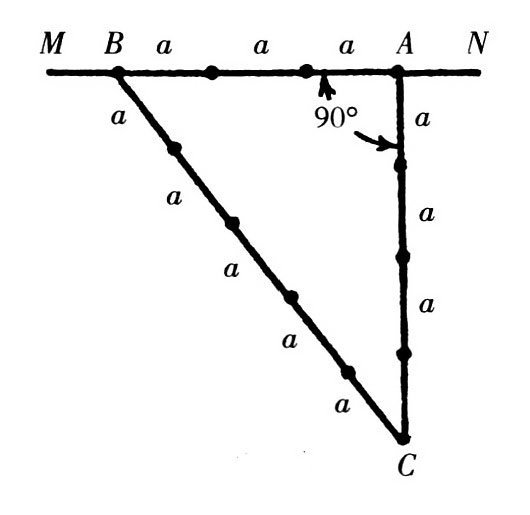
这是一个非常古老的方法，在几千年以前建造埃及金字塔的人就使用过这个方法。它的原理很简单，如果三角形的边长之比为3:4:5，那它必然是直角三角形。根据勾股定理，很容易证明，因为

3²+4²=5

除了3，4，5，还有很多正整数a，b，c也满足下面的等式：

a²+b²=c

由勾股定理，满足上述条件的数a，b，c被称为“勾股弦数”。其中，a，b称为三角形的“直角边”，有时也叫“勾”或“股”，c称为三角形的“斜边”，有时也叫“弦”。

显然，如果a，b，c是满足上面关系的整数，那么pa，pb，pc也满足上面的关系，这里的p是整数。反之，如果满足上面关系的a，b，c有一个共同的乘数，那么把这个乘数约去，就会得到另一组满足上述关系的整数。所以，这里只讨论最简单的勾股弦数，即互素的勾股弦数。

容易知道，在边长a，b，c中，直角边a，b必定一个是偶数，一个是奇数。因为如果a，b都是偶数，那么（²²a+b）也一定是偶数，这样的话，a，b，c一定有公约数2，这跟前面假设的a，b，c互素是矛盾的。所以，在直角边a，b中，一定有一个是奇数。

那么，有没有可能直角边a，b都是奇数，而斜边c是偶数呢？同样的方法可以证明，这也是不可能的。事实上，如果两个直角边a，b都是奇数，不妨把它们表示为

（2x+1）和（2y+1）

那么，它们的平方和为

4x²+4x+1+4y²+4y+1=4(x²+x+y+y²)+2

如果把上面的结果用4除，会得到余数2。但是我们知道，如果一个数是偶数，那么它的平方一定可以被4整除。所以，这个平方数不会是一个偶数的平方。也就是说，如果a，b都是奇数，那么c一定也是奇数。

综上所述，在a，b，c中，直角边a，b必然有一个是奇数，有一个是偶数，而斜边c必然是奇数。

不妨假设直角边a是奇数，b是偶数，根据a²+b²=c²

可以得出a²=c²-b²=(c+b)(c-b)

右边的两个乘数(c+b)和(cb)互为素数。

对于上面的结论，可以用“反证法”证明。假设（c＋b）和（c－b）有一个共同的素因数，那么它们的和

(c+b)+(c-b)=2c

差

(c+b)(cb)=2b

积(c+b)(c-b)=a²

应该都能被这个素因数整除，换句话说，2c，2b，a²有公因数。而a为奇数，所以这个公因数不可能为2，也就是说，a，b，c应该有公因数，这跟假设是矛盾的。所以，(c+b)和(c-b)一定互为素数。

既然这两个数互为素数，它们的乘积又是某个数的平方，那么它们自身也应该是某个数的平方，也就是说

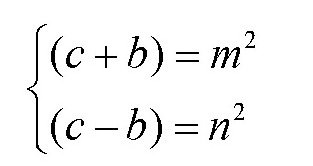
解这个这方程组，可得

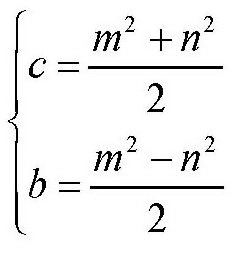
所以

a²=(c+b)(cb)=m²n²

a=mn

这样，就得出了a，b，c的值，它们是

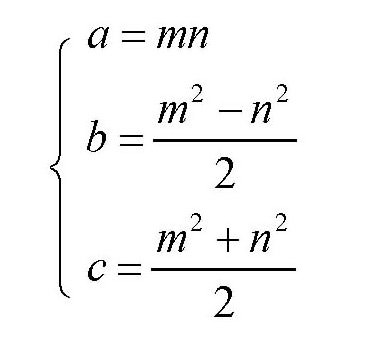
其中m，n都是奇数，且互为素数。

反过来说，对于任意互为素数的奇数m和n，都可以利用上面的公式得出整数勾股弦数a，b和c。

下面列出了这样的一些勾股弦数：

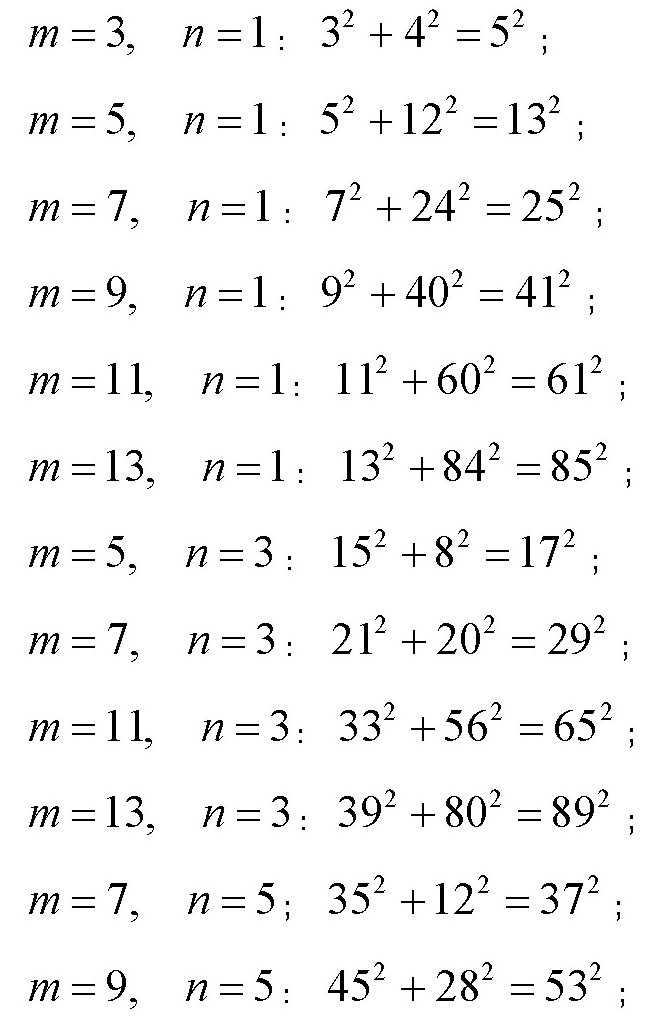
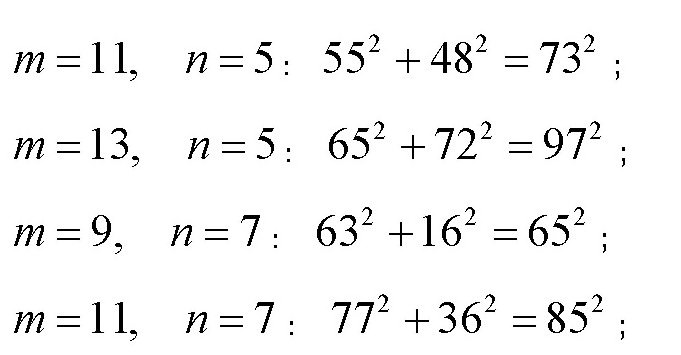
从这些数可以看出，它们都是没有公因数的整数勾股弦数，而且都比100小。

勾股弦数有很多有意思的特性，比如：

如果一条直角边小于3，另一条直角边小于4，那么斜边应该小于5。

对于这个特性，很容易验证，读者可以自己证明一下。