【题目】你在商店里看中了一件衣服,这件衣服的价格是19卢布。你身上的钱都是面值为2卢布的,而商店里的钱都是面值为5卢布的,那么你该怎么付钱呢?
其实这个题目可以转化为:你应该给商店几张2卢布的钞票,商店找给你几张5卢布的钞票,使得商店收到的钱数正好是19卢布。题目要求的未知数有两个:一个是2卢布面值钞票的张数x,另一个是5卢布面值钞票的张数y。根据题意,只能得到一个方程,即
2x-5y=19
对于上面的方程来说,有无数个解,但是,能否找到x和y都是正整数的解呢?这并不是件很容易的事,因此才会寻找求解这类“不定方程”的方法。首次将这种方法引入代数的是古希腊著名数学家丢藩图,所以,我们也称这类方程为“丢藩图方程”。

【解答】下面,我们就这个例子来说明这类方程的解法。
现在的问题是求方程
2x-5y=19
的解,其中x和y都是正整数。
首先,把方程进行变形,即
2x=19+5y
所以
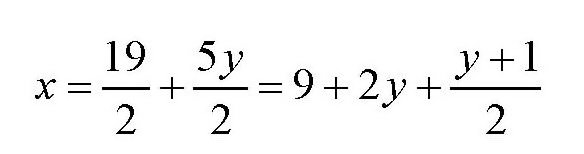
在上式的右边,9和2y都是正整数,要想x也是正整数,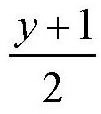
必须是正整数才行。
设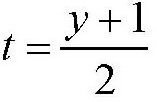
,则有
x=9+2y+t
那么
2t=1+y
y=2t-1
把前面式子中的y用上式中的(2t-1)代替,则有
x=9+2(2t-1)+t=5t+7
现在来看下面的方程组
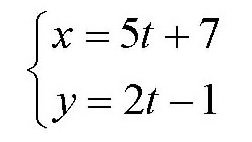
可以看出,如果t是整数,x和y就一定是整数。这里的x和y必须是正整数,也就是说,它们都大于0,即
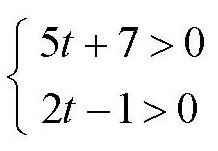
解上面的不等式,得到
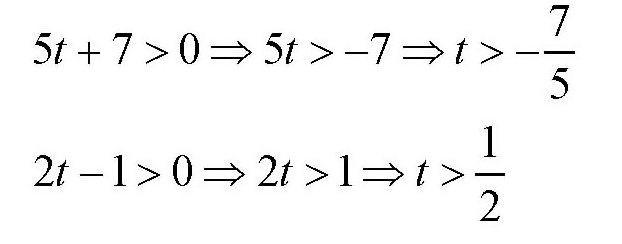
所以,t的取值范围是
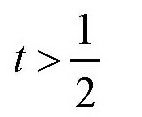
由于t是整数,所以t可以取下面的数值:
t=1,2,3,4,…
对应的x和y的值分别为:
x=5t+7=12,17,22,27,…
y=2t-1=1,3,5,7,…
现在,就知道该如何付款了。
你给商店12张2卢布面值的钞票,商店找回你1张5卢布面值的钞票:
12×2-5=19
或者你给商店17张2卢布面值的钞票,商店找回你3张5卢布面值的钞票:
17×2-3×5=19
等等。
从理论上讲,这个题目的解有无数个。但是,对于你和商店来说,不可能有无穷多的钞票,比如说,你们双方都只有15张钞票,这时就只有一个解:你给商店12张2卢布面值的钞票,商店找回你1张5卢布面值的钞票。
在这个题目中,如果条件变一下,比如,你只有5卢布面值的钞票,而商店只有2卢布面值的钞票,读者可以自己计算一下,很容易得到下面的解:
x=5,7,9,11,…
y=3,8,13,18,…
实际上:
5×53×2=19,
7×58×2=19,
9×513×2=19,
9×518×2=19,
…
其实不用重新计算,通过借助一点简单的代数方法,就能从母题的解法中求出上面题目的解。在上面的题目中,你付给商店5卢布面值的钞票,商店找回2卢布面值的钞票,就相当于你付了-2卢布面值的钞票,商店找回给你-5卢布面值的钞票。所以,仍然可以用前面的方程
2x-5y=19
来求解。但这里要求x和y都是负数。
所以,由方程组
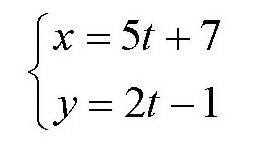
得到
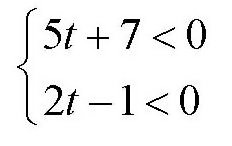
解得
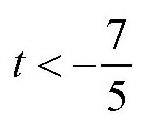
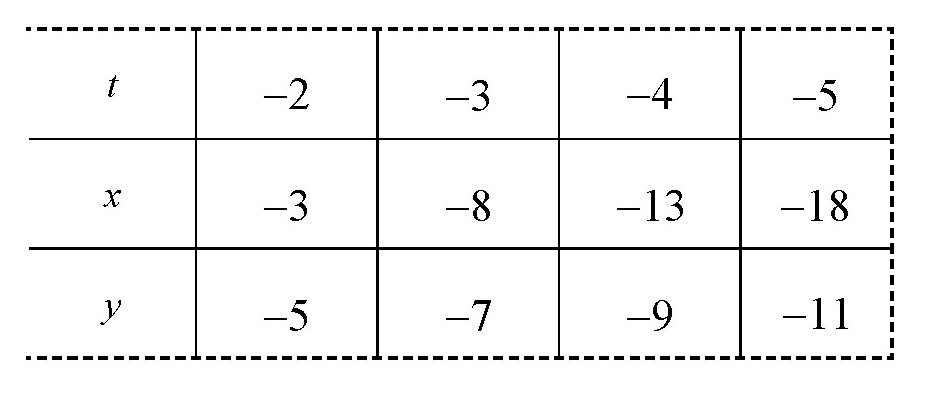
取t2,-3,-4,-5,=…就可以得出x和y的值(见下页表格)。
对于第一组解:x=-3,y=-5,意思就是:你付给商店-3张2卢布面值的钞票,而商店找回你5张5卢布面值的钞票,换句话说,你付给商店5张5卢布面值的钞票,而商店找回你3张2卢布面值的钞票。对于其他的几组解,也可以用同样的方法进行解释。