其实,我们可以用几何学知识证明:在周长相等的情况下,对于一个正多边形,边数越多,其面积越大。如果在一定的周长下,圆的面积最大。如果巴霍姆跑的路线是圆形(这个圆的周长是40俄里),那么他就可以得到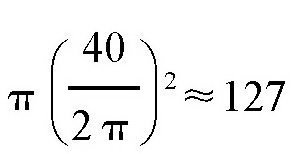
平方俄里的土地。
在周长相等的情况下,没有一种图形比圆的面积更大。
也许有的读者朋友想知道这是为什么。下面,我们就来对这一结论进行一下证明,看看圆到底是不是真的有这样的特性。
需要说明的是,下面的这种证明方法并不是十分严格,不过,可以帮助我们理解圆的这一特性。
需要证明的题目是:在周长为定值的情况下,圆的面积是最大的。
首先,我们需要确定一点,就是这个图形必须是凸边的。也就是说,它所有的弦都在这个图形的里面。如 图 所示,假设有这样一个图形AaBC在这个图形中,弦AB在图形的外面,那么如果我们用弧a来代替弧b,对于这个图形来说,周长并没有变化,但是它的面积却明显变大了。所以,在周长为定值的情况下,图形AaBC的面积绝对不是最大的。
如果我们找到了这个图形,它的面积最大,那么这个图形一定是凸边的。下面,我们再来说明它的另一个特性:如果在这个图形中存在一条弦,使它的周长二等分,那么也必然使它的面积二等分。如 图 所示,假设图形AMBN是这个面积最大的图形,并且,假设它的周长被弦MN二等分,下面,我们就来证明图形NAM的面积等于图形MBN。
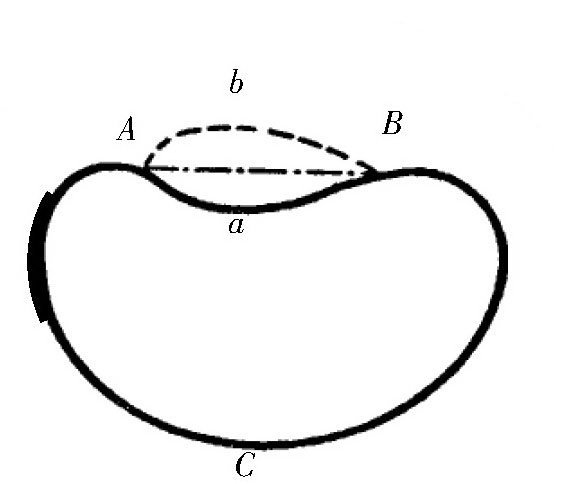
图 当周长相等时,最大面积的图形一定。
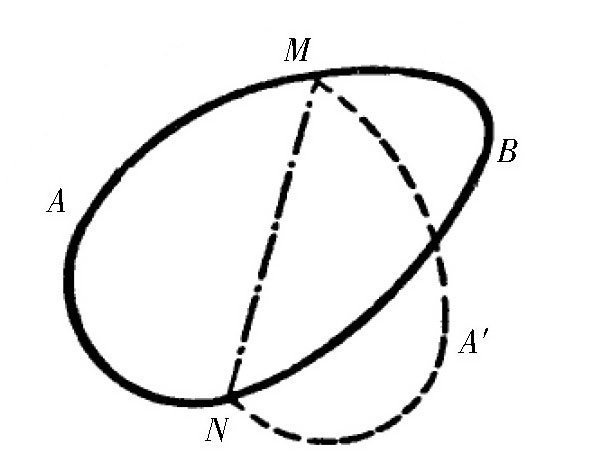
图 如果一条弦把一个具有最大面积的凸边形的周长二等分,那这条弦也一定将面积二等分。
首先,我们假设其中的一个图形面积大一些,比如,AMN>MBN。如果沿着MN把NAM折过去,并根据图形MAN作一个全等的图形MA′N。这个新图形AMA′N图形AMBN的周长相等,但面积比图形AMBN大。那就说明图形AMBN并不是我们要找的图形,因为它不是相同周长中面积最大的圆。
在继续讨论之前,我们需要证明下面这个补充定理:如果已经知道了三角形的两个边长,那么在所有以它们为其中两条边的三角形中,面积最大的三角形是以它们为两个直角边的三角形。
怎么来证明这一定理呢?我们不妨假设这两条边分别为a和b,它们的夹角为C。那么,这个三角形的面积就可以表示为:
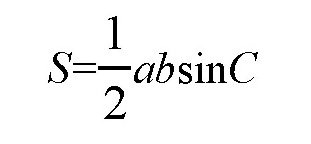
由上式可以看出,如果两条边a和b是已知的,那么三角形的面积就取决于角C的值,很明显,sinC取最大值1的时候,面积S是最大的。这个时候,角C的值必定是90°,也就是在两个边成直角时。现在证明:在所有周长相等的图形中,圆的面积最大。如 图 所示,假设存在这样一个非圆图形MANBM,在周长相等的情况下,它的面积最大。
第1步:我们作出可以把周长二等分的弦MN。在前面,我们证明过,这时图形的面积也会被二等分。
第2步:我们把图形的MKN部分沿着MN折起来,得到了对称的图形MK′N,所以图形MNK′M跟原来的图形MKNM周长和面积都是相等的。而弧MKN并不是一个圆的半周,所以,它上面的任何一个点跟点M和N的连线都不可能构成直角。
第3步:假设点K就是这上面的一个点,它的对称点为K′,所以,角K和角K′都不是直角。在线段MK、KN、MK′和NK′长度不变的情况下,移动它们的位置,使它们的夹角K和K′为直角,则这两个直角三角形全等。
第4步:如 图 所示,把两个三角形对应的弦合并起来,并把图形中的阴影部分合并到M′K、′KN′、N′K′、K′M′的外面。这样,我们就得到了图形M′KN′K′M′,很明显,这个图形的周长跟原来的图形也是相等的。但是,由于三角形M′KN′和M′K′N′是直角三角形,根据前面的结论,我们知道它们的面积比三角形MKN和MK′N大。所以,图形M′KN′K′M′的面积也比原来图形的面积大。
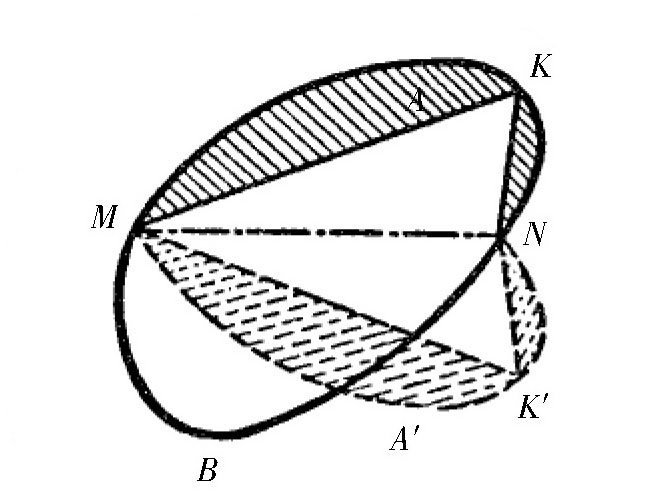
图 假设一个非圆形的凸形面积最大,能否实现?
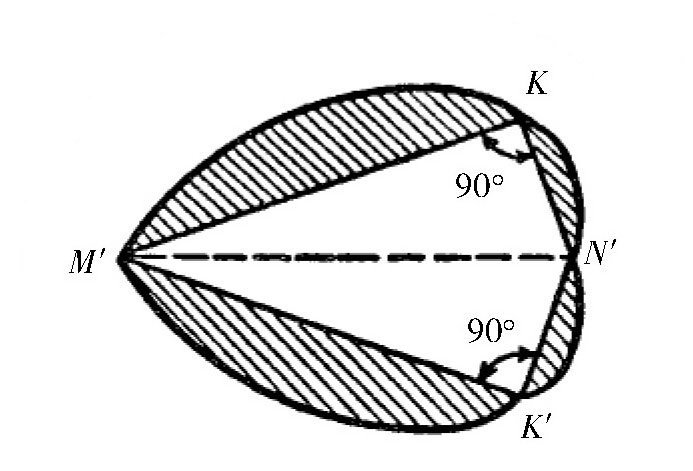
图 这里需证明,在周长相等的情况下,最大面积的图形仍然为圆形。
因此,我们前面的假设是错误的。由此我们可以得出结论,如果这个图形不是圆形,它的面积就不是最大的。
综上所述,在周长相等的各种图形中,圆的面积是最大的。
另外,我们还可以证明:在面积相等的各种图形中,圆的周长最短。至于证明的方法,可以采用前面证明正方形的方法。
