在科学研究中,我们会使用到各种各样的仪器,悬锤和摆可能是最简单的了。不可思议的是,虽然它们非常简单,但却可以帮助我们得到令人惊叹的结果。比如,借助它们,我们可以把思想深入到地球的内部,探测到地下几万米的地方。对于这一点,我们除了惊叹,还应该感叹。要知道,世界上最深的钻井也只能到达几千米的地方,跟悬锤和摆所探测的深度比起来,差远了。
悬锤的这一功用是可以用力学原理解释的。如果地球是完全均匀的,那么我们可以计算出悬锤在任何一个地方的方向。但是,我们知道,地球是不均匀的,在地表或者地下,它的质量分布是有差异的,所以实际方向就会跟理论方向有偏差,如 图 所示。在高山附近的某个点,悬锤会偏向山顶的方向,而且,在距离山顶越近的地方,由于山的质量越大,偏得就会越多,如图所示。反过来,如果地下有空隙,悬锤就会被吸引到旁边去,就好像空隙会排斥悬锤一样。这是因为有了空隙,旁边的质量要大一些,于是就把悬锤吸引了过去。而且,不仅空隙会排斥悬锤,只要它下方物质的密度比地球地层的密度小,也会受到排斥,只不过它受到的排斥力比较小而已。由此可见,我们可以通过悬锤来研究地球内部的构造。
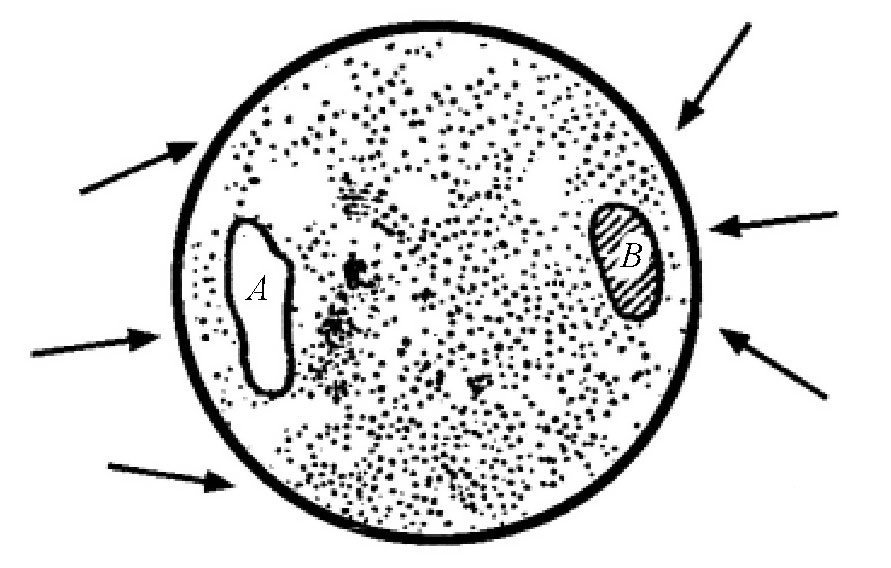
图 地层里的空隙A和密层B都会使悬锤产生偏斜。
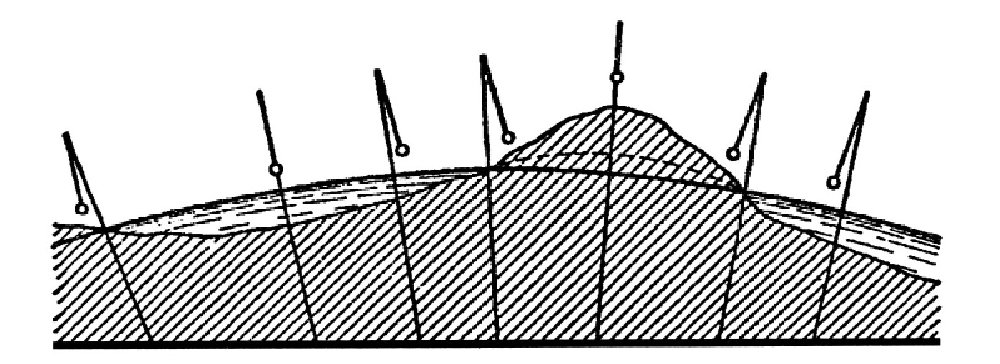
图 地面的起伏和悬锤方向的变化关系。
除了悬锤,摆也可以用来进行这方面的研究,而且,它的作用更大。对于摆来说,只要摆动的幅度不是很大,一般在几度之内,那么不管它的摆动幅度是多少,它摆动一个来回的时间(也就是摆动周期),都与摆动的幅度无关,而只与摆的长度和它所在位置的重力加速度有关。当摆的摆动幅度比较小的时候,它完成一次全摆动,也就是周期T与摆长l、重力加速度g的关系为:
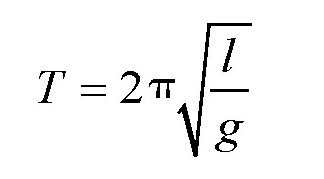
其中,如果摆长l的单位是米,那么重力加速度的单位就应该取米/秒2。
在研究地质结构时,我们通常使用“秒摆”。这种“秒摆”每秒向一个方向摆动一次,一个来回算两次,也就是摆动周期为2。所以,可以得到下面的式子: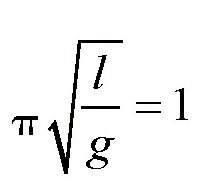
,变化可得:
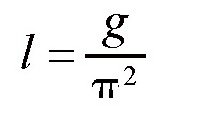
从式子中可以看出,摆长与重力是成正比关系的,重力的变化可以在摆长上体现出来。在不同的地方,需要通过改变摆长,保证摆每秒摆动一次。在重力加速度变化非常小时,也可以使用这种方法。其实,这个问题比我们想象得要复杂多了,所以在本文中不做深入研究和讨论,这里只举几个非常有意思的例子。
如果在海岸边进行这个实验,我们可能会认为:悬锤应该偏向大陆一侧,就像它会偏向山顶的方向一样。但是,有人通过实验证实,这个想法是错误的。实验发现,在海洋和海岛上,重力加速度要比海岸边大,海岸边的重力加速度又比远离海岸的大陆大。这是什么原因呢?很明显,这说明了一个问题:远离海岸的大陆底下的地质比海洋下的要轻。正是基于这一点,地质学家对我们生活着的地球的内部构造和外壳岩石成分进行了推测。
如 图 所示,这种方法还被用于查明“地磁异常区”的原因,并且取得了非常好的效果。

图 异常重力测量图。右上图是可变引力仪器原理示意图。
此外,在一些跟物理毫不沾边的学科中,物理学也有很实际的应用,比如,下面的例子就非常典型。
我们都知道,地球并不是圆形的,在构造上也不是很均匀,这对于人造地球卫星的运动是非常不利的。从理论上来说,如果人造地球卫星是在山脉的上空或者地质密度非常大的地域上空飞行,那么它受到的地球引力应该比较大,所以运动速度也应该比较快。当然了,只有当人造地球卫星在比较高的高空运行的时候,才具有这个特性。因为在比较高的高空,空气阻力不会影响卫星的自然运动。通过人造地球卫星运动速度的核变化,人们可以非常精确地测量出重力的变化。
