有一个奇怪的现象,虽然太阳比月球距离我们更遥远,但我们可以很容易地得出太阳的质量,要想得出月球的质量,则需要花一番工夫。
那么,太阳的质量如何计算呢?我们知道,质量为1克的物体对1厘米外另一物体的引力是
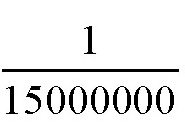
毫克。根据万有引力定律,如果这两个物体的质量分别是M和m,它们的距离是D,那么,它们之间的引力f为:
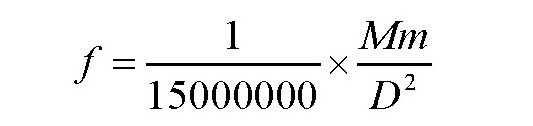
如果把上式中的M用太阳的质量代替,m用地球的质量代替,D用日地距离150000000千米代替,则可以计算出太阳与地球之间的引力是:
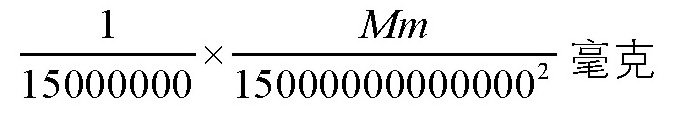
其实,这个引力也是地球沿绕日轨道运行时的向心力。根据力学公式,我们知道,向心力为
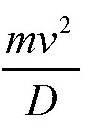
(单位:毫克),其中,m为地球的质量(单位:克),v为地球的公转速度,等于30千米/秒(也表示为3000000厘米/秒),D为日地之间的距离。所以有:
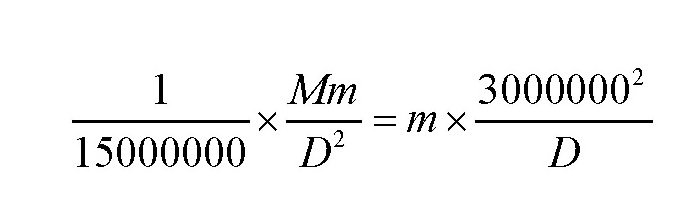
解得:
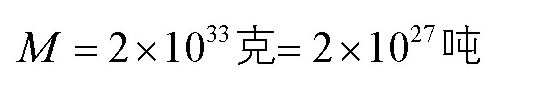
用这个数字除以地球的质量得
此外,根据开普勒第三定律和万有引力原理,我们可以得出下面的公式:
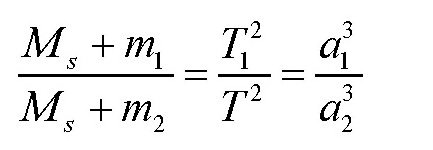
其中,Ms为太阳的质量,T为行星的恒星周期(这里的恒星周期指的是站在太阳上看到的行星围绕太阳旋转一周所用的时间),a为行星到太阳的平均距离,m为行星的质量。如果把这一公式运用到地球和月球上,则有:
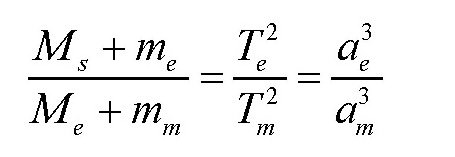
把
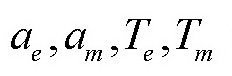
的值代入上式。为便于计算,我们可以把分子中比太阳质量小得多的地球质量和分母中比地球质量小得多的月球质量忽略不计,从而得出一个近似值,即:
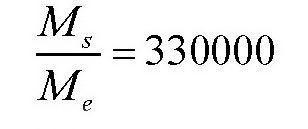
地球的质量是已知的,所以,我们可以计算出太阳的质量,大概是地球的330000倍。然后,用太阳的质量除以它的体积,就可以得出太阳的平均密度,大概是地球的1/4。
可见,测定太阳的质量是比较容易的。但是,如果想测定月球的质量,就不那么容易了。有位天文学家说过这样的话:“虽然月球是离地球最近的星体,但是,要想测出它的质量,比最远的海王星要困难多了。”这是因为,测定月球的质量需要通过非常复杂的方法才行,其中一种方法是通过比较月球和太阳引起的潮汐高低来进行。
这个方法的原理是:潮汐的高度跟引起这一现象的天体质量和距离有关。太阳的质量和距离以及月球的距离都是已知的,于是,我们就可以通过比较二者的高度来推算出月球的质量。在后面的章节中,我们会提到具体的算法,这里先给出结果:月球的质量大概是地球的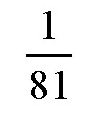
,如图所示。
图月球的质量是地球的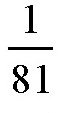
月球的半径也是已知的,我们可以计算出月球的体积,大概是地球的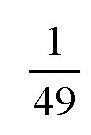
。所以,月球跟地球的平均密度之比就是:
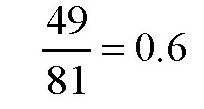
可以看出,跟构成地球的物质比起来,构成月球的物质疏松多了,但如果跟太阳比,则紧密得多。事实上,月球的平均密度比很多行星都要大。
