类似于上面的特征,还有一些由多位数字组成的长串数尾,在经过连乘后仍保持不变,而且,这些数尾的长度甚至可能是无限的。
我们已经知道,具有这种特性的两位数有25和76,那么,有没有具有这种特性的3位数呢?我们可以通过下面的方法来寻找。
假设在76的前面的数字为k,那么这个3位数可以表示为下面的形式:
100k+76
于是,以这个3位数为末尾的数就可以表示为(1000a+100k+76),(1000b+100k+76),等等。
那么,它们的乘积就是
(1000a+100k+76)(1000b+100k+76)=1000000ab+100000ak+100000bk+76000a+76000b+10000k2+15200k+5776
从上面的式子可以看出,除了最后两项,前面的各项都是1000的倍数,也就是说,每项后面都有3个0。那么,如果以下两项之差,即
15200k+5776(100k+76)
能被1000整除,那么,所得乘积的末尾就还是(100k+76)。而上面的式子为
15100k+5700=15000k+5000+100(k+7)
很明显,当k=3时,上式可以被1000整除。
所以,所求的3位数是376。也就是说,376的任何次方得出的数一定以376为末尾,比如
3762=141376
同样的方法,可以找到符合条件的4位数。假设376的前面的数字为l,那么,问题就变为:当l等于几的时候,下面的乘积
(10000a+1000l+376)(10000b+1000l+376)
以(1000l+376)为末尾?把上式的括号去掉,并把10000的倍数的项舍去,最后剩下下面两项:
752000l+141376
上式与(1000l+376)的差为
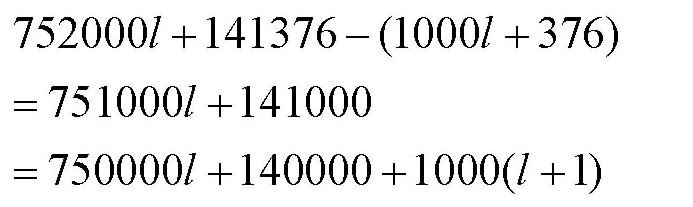
只有当上面这个数可以被10000整除的时候,所得乘积的末尾才是(1000l+376)。很明显,这时候l=9。
也就是说,所求的4位数是9376。
同样的方法,我们可以求出满足这一条件的其他多位数,比如说,5位数09376,6位数109376,7位数7109376,等等。
只要在这些数的前面加上一位,就可以一直计算下去,从而得到一个无限多位的这样的“数”:
……7109376
对于这样的数来说,同样可以进行一般的加法或者乘法运算,因为这些数是从右向左写的,而加法或乘法的竖式运算也是从右向左进行的。并且,当两个这样的数进行加法或乘法运算时,它们的和或者乘积可以去掉任意多的数字。
更加有意思的是,对这个无限长位数的“数”而言,下面的方程是成立的:
x2=x
这看起来有点不可思议,但确实如此。由于这个数的末尾为76,所以它二次方的末尾也应该是76。同样,我们可以得出,这个数二次方的末尾也可以是376,或者是9376,等等。也就是说,这个“数”的二次方中逐个减去一些数字,就可以得到一个与x=……7109376相同的数。所以,我们可以得出结论:
x2=x
以上分析了以76为末尾的“无限长”的数。同样的方法,我们可以找出以5为末尾的这类数,它们是
5,25,625,0625,90625,890625,2890625
最后也可以得到一个满足x2=x的无限多位的“数”:
……2890625
而且,这个无限多位的“数”还“等于”:
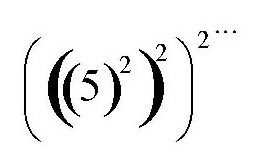
可以这样说明这个数:在十进制中,除x=0和x=1外,方程x2=x还有两个无限的解:
x1=……7109376LL,x2=……2890625
