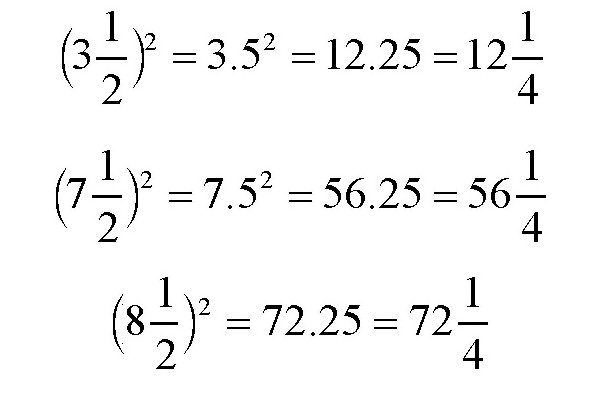了解速乘法,借助简单的代数变换减少计算量

对算术来讲，要想严格证明其中某些判断是否正确，并不能依靠它自身进行，这就需要用到代数的方法。比如说，有些简便的算法，某些数字的有趣特性，判断一个数是否能被整除，等等，这些算术命题往往需要用代数方法来进行证明。

为了简化计算，运算熟练的人常常借助一些简单的代数变换来减少计算量，比如要计算²988。

可以用以下方法计算：

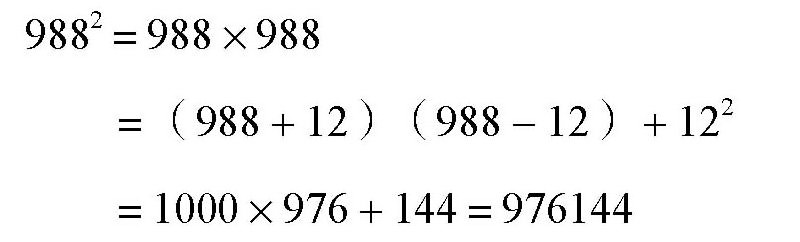
很明显，此处用到了如下的代数变换：

a²=(a+b)(a-b)+b²

有了上面的公式，我们可以进行很多类似的运算。比如

27² = (27 + 3)(27 -3) + 3² = 729，

63² = (63+ 3)(63-3) + 3² = 3969，

18² = 20×16 + 2² = 324，

37² = 40×34 + 3² =1369，

48² = 50×46 + 2² = 2304，

54² = 58×50 + 4² = 2916。

再看一个例子，计算986×997。

可以通过以下方式计算：

986×997=(986-3)×1000+3×14=983042

以上算法的依据是什么呢？在上面的计算中，我们进行了下面的变换：

986×997=(1000-14)×(1000-3)

按照代数法则，把上面的括号去掉，就变成：

1000×1000－1000×14－1000×3＋14×3

接着进行变换：

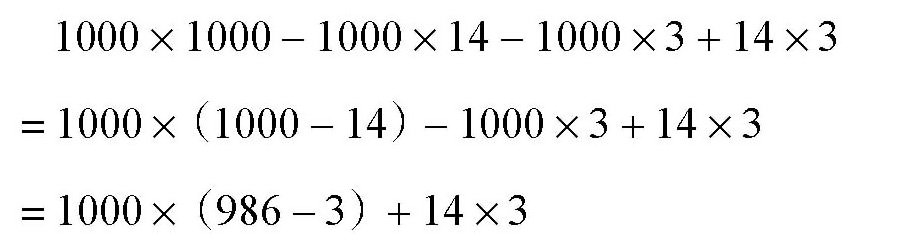
最后一行就是前面的算式。

如果相乘的两个三位数的十位和百位相同，而个位之和等于10，那么它们的乘法很有意思。来看一个例子，比如计算783×787。

可以这样计算：

78×79=6162

3×7=21

所以，上面乘法的计算结果就是616221。

这种算法的依据又是为什么呢？通过下面的算式就可以看明白了：

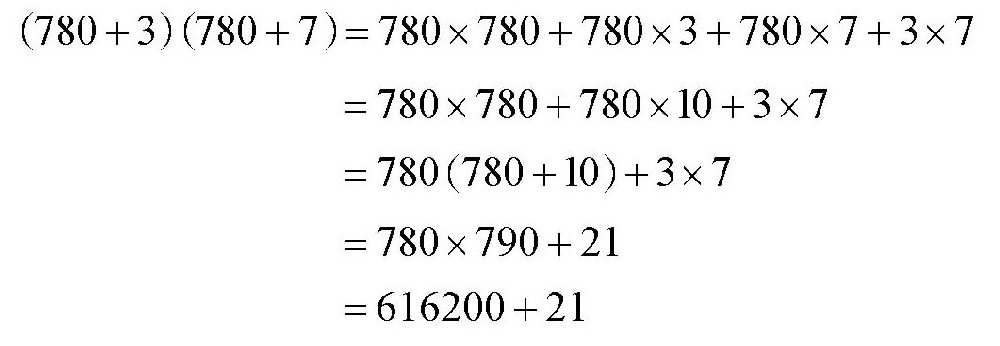
关于这类数的乘法，还有另一种简单的计算方法：

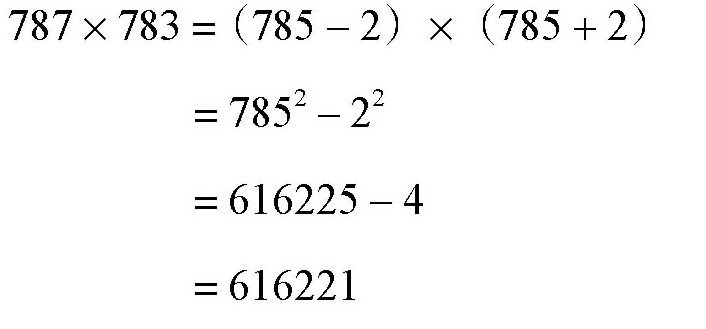
只不过在这个方法中，需要计算785的平方。

如果一个数的末位是5，那么，可以用下面的方法计算它的平方，比如

35²：3×4=12，结果是1225；

65²：6×7=42，结果是4225；

75²：7×8=56，结果是5625。

以上方法的计算规则为：把这个数的十位数乘以比它大1的数写在前面，然后在后面写上25。

我们可以对此进行严格的证明。假设这个数的十位数是a，那么这个数可以表示为：

10a+5

这个数的平方就是：

100a²+100a+25=100a(a+1)+25

式子中的a(a+1)就是十位数和比它大1的数的乘积，得到的结果乘以100再加上25，就相当于在前面的乘积后面直接写上25。

如果一个整数后面带一个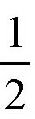

，那么，也可以用上面的方法来求平方。比如