我们知道,河水总是在运动着,并不断冲刷着河岸。同时,它还会把冲下来的碎块带到河床的其他位置。在水流的作用下,河底的石块会不停翻滚。有时候,这些石块非常大。可见,水的能力是很强大的,但是并不是所有的河流都可以做到这一点。比如,平原上流得很慢的河流,它带起来的可能只是一些很细的沙粒。不过,只要水流的速度稍微变大一些,就可以大幅度提高水流携带石块的能力。要是河水的速度增加到原来的2倍,那它就可以带走一些大的鹅卵石。如图所示,这是山涧中的急流,它可以带走重达1千克甚至更重的圆石。对于这个现象,我们该如何理解呢?
说到这里,我们要提到一个有趣的力学定律,叫艾里定律。它是这么说的:如果水流的速度增加到原来的n倍,那么水流可以带走的物体的质量将是原来的n6倍。

图 山涧中的急流可以带走石块。
下面,我们就来说明一下,为什么在艾里定律中会出现6次方这一少见的比例关系。
为方便说明,我们假设河底有一块边长为a的立方体石块。如图所示,石块的侧面S受到了水流压力F的作用。力F想把石块沿轴AB翻转过去。这时,石块的重力P会反作用于它,阻止它沿轴AB翻转。根据力学原理,要想保持石块的平衡,力F和力P对轴AB的力矩必须相等。这里的力矩指的是:作用力与它到轴的距离的乘积。所以,对于力F,它的力矩等于Fb,而对于力P,它的力矩等于Pc。而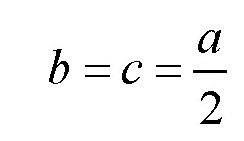
,所以,只有当: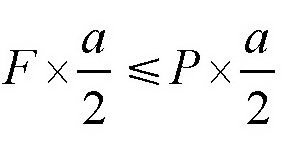
,也就是F≤P时,石块才能保持平衡。我们知道,Ft=mv,其中,t表示力F作用的时间,m表示在这段时间里作用于石块的水的质量,v表示水流的速度。

图 边长为a的正方体石块在水流里受到的作用力示意图。
根据流体动力学,我们可以得到下面的关系:在跟水流方向垂直的平面上,水流对它的压力和这个平面的面积成正比,和水流速度的平方也成正比,即:
F=ka2v2
根据阿基米德原理,我们知道:
P=a3d-a3=a3(d-1)
那么,前面的那个平衡条件就可以表示为:
ka2v2≤a3(d-1)
化简可得:
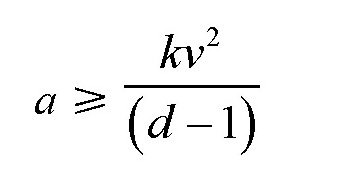
也就是说,当方石块的边长与水流速度的二次方成比例,并大于这一比例关系时,它才有可能抵抗住水流的冲击。
我们知道方石块的质量与a3成比例,而(v2)v3=v6,所以水流可以带走的方石块的质量跟水流速度的6次方成比例。
这就是艾里定律中的比例关系。在上面的分析中,我们只是以立方体石块为例进行了证明。通过证明,我们知道:对于任意形状的物体,这个定律都是适用的。
关于艾里定律,我们可以举个例子来计算一下。假设有3条河流:第一条的水流速度是第二条的一半,第二条的水流速度又是第三条的一半。也就是说,它们的水流速度是1∶2∶4的关系。根据艾里定律,这3条河流可以带走的石块的质量应该有下面的比例关系:
1:26:461:64:4096
所以,如果第一条平静的河流可以带走重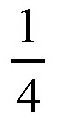
克的沙粒,那么第二条水流速度是它2倍的河流就可以带走重16克的石子,而第三条水流速度是第一条4倍的河流就可以带走上千克重的大石块。
