1 7 2 6 年,荷兰物理学家丹尼尔·伯努利首先提出了这样一个原理:当水流或者气流的速度小时,其对外的压力就大;当速度大时,对外压力就小。图 就是这个原理的图形解说。当然,在现在来看,这个理论要成立存在很多局限,在此我们就不一一赘述了。
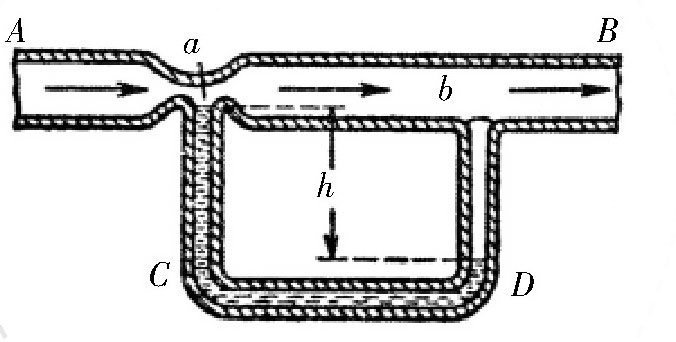
图 伯努利原理图示。
在图中,空气顺着AB管进入。气流在管的截面比较小的地方(a处),速度就会比较大;而在管的截面比较大的地方(b处),速度就会比较小。在速度大的地方,压力就小;而在速度小的地方,压力就大。由于空气压力在a口处时比较小,所以在C管中的液面高度就会上升。与此同时,D管中的液体在b处强大的空气压力下,液面高度就会下降。
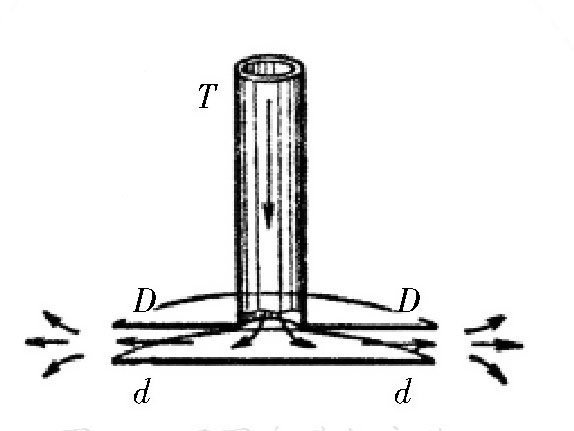
图 用圆盘进行实验。
在 图 中,我们将T管牢牢固定在铜制圆盘DD上,而圆盘dd跟T管并不相连。空气会顺着T管进入圆盘DD和圆盘dd的夹层中。随后,它会通过圆盘dd。虽然这两个圆盘之间的气流速度会很大,但气流在接近圆盘边缘时,速度会迅速减小,因为气流在流出两个圆盘空隙之间后,它获得的空间会迅速增大,空气的压力也就会逐渐减小了。而位于圆盘周围的空气压力是很大的,就是因为这里的气流速度很小。如果位于圆盘之间的空气压力很小,气流速度也会很大。所以当圆盘周围的空气作用在圆盘上的压力较大时,就好像有一个推力在努力想推开这两个圆盘。如果从T管流出的气流很强,圆盘DD吸引圆盘dd的力量就会很大。 另外,如果我们用线轴或者圆纸片来做这个实验,实验会更加简单。为了使两个圆纸片能固定住,不会滑到一边去,可以使用一个大头针,穿过线轴的槽,把纸片钉住。
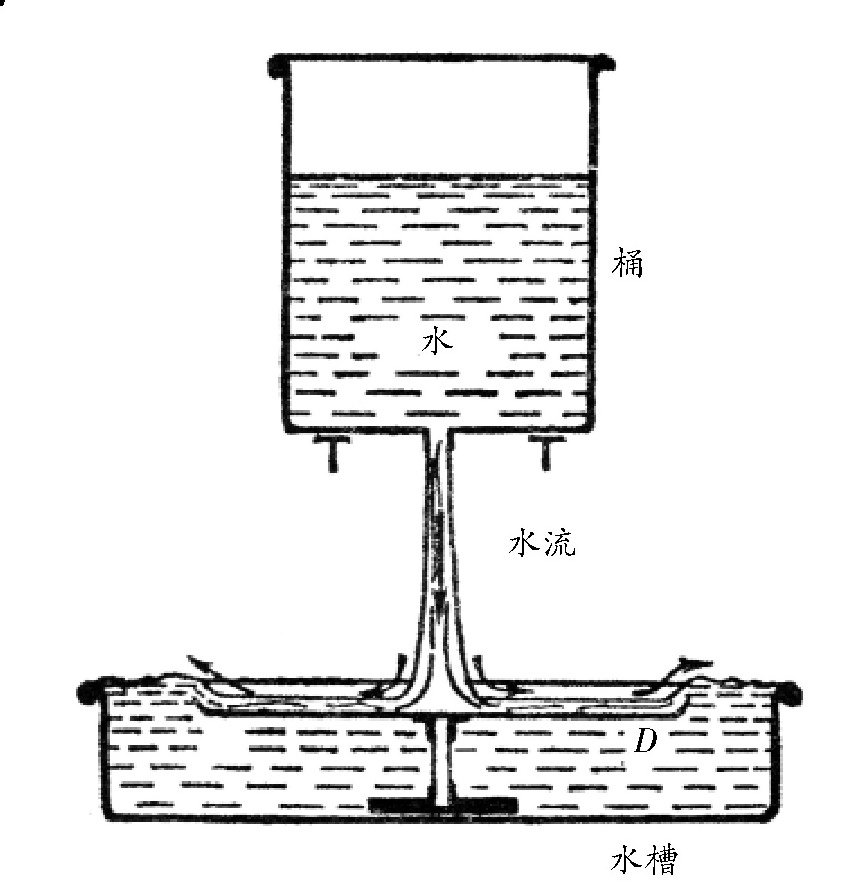
图 水桶TT里的水流到圆盘DD上时,轴P上的圆盘会升起来。
图 与图演示的实验很相似,只不过图里有水。假如圆盘DD的边缘是向上弯曲的,那么在盘中快速流动的水就会从较低的地方一直上升到跟上面水槽里的静止水面一样高。这样的话,与圆盘里的水相比,下面的静水会受到更大的压力。在压力作用下,圆盘就会上升。而P轴的作用是保证圆盘不向两边移动。
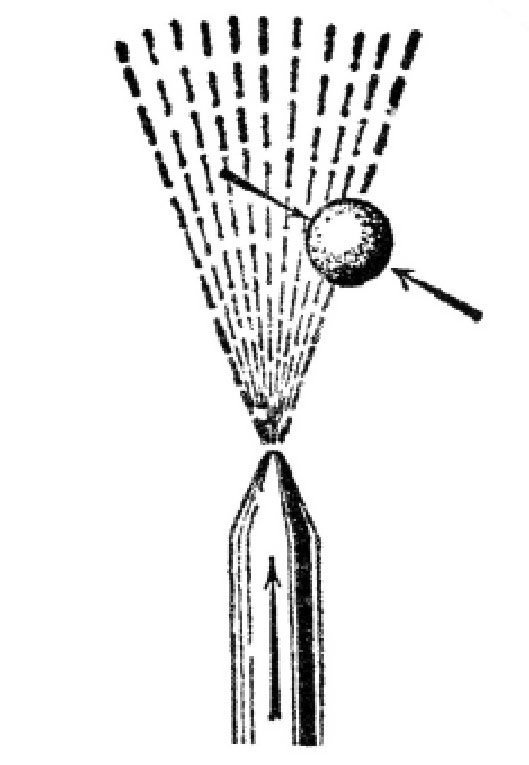
图 被气流支撑着的小球。
图 中演示的是一个小球漂浮在气流中。由于受到气流的不断冲击,小球就不会落下来。一旦小球离开了气流,它又会被周围的空气推回去,这也是因为周围空气的速度小但压力大造成的,而气流中的空气的速度会大一些,压力却要小很多。
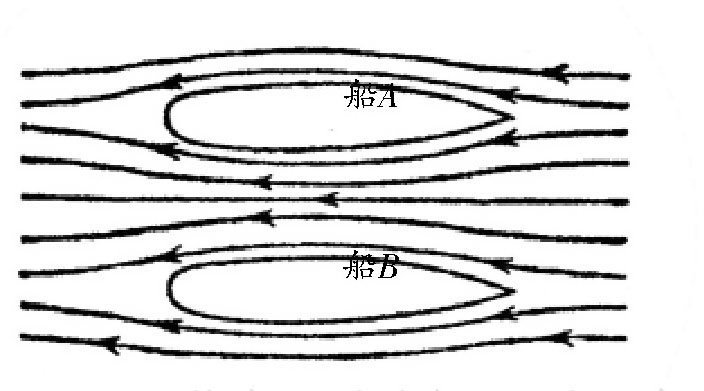
图 两艘并行的船会相互吸引。
图 所画的是两艘船。这两艘船并行在静止的或流动的水中。因为这两艘船之间的水面比较窄,所以这里的水流速度比在两船外侧的水流速度要大,而受到的压力比两船外侧要小。在这种情况下,这两艘船在船周围压力较高的水的力量作用下,会挤到一起去。海员们都知道,两艘并排行驶的船,会发生互相吸引的现象。
如果两艘船不是并行,而是其中一艘行驶在另一艘的前面,那情况就会更加严重(图)。本来迫使两艘船相互靠近的两个力会造成船身转向,在一个很大的力的作用下,船B会转向船A。在这种情况下,舵手根本来不及改变船的航向,所以两船相撞基本是无法避免的。
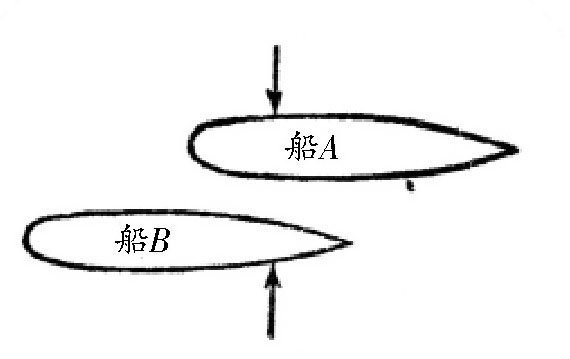
图 两艘船一前一后前进的时候,船B会转向船A驶去。
针对图中的情况,还可以用另外一个实验来说明:在两个很轻的橡皮球之间吹气 (图),你会发现这两个球会相互靠近或撞击。
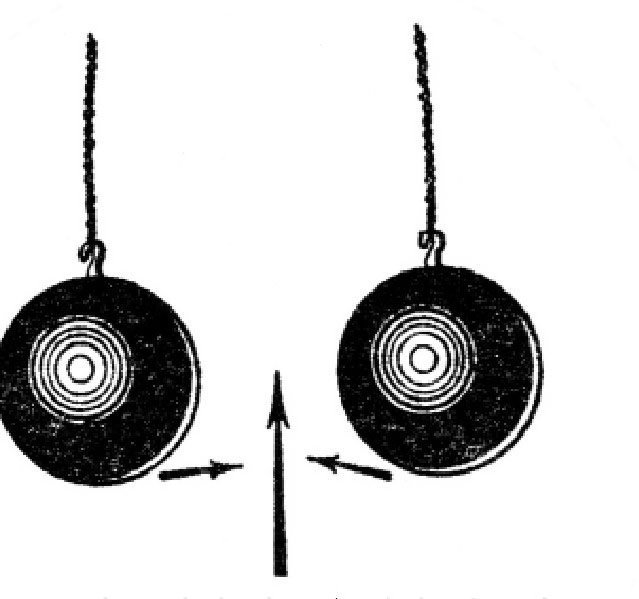
图 向两个气球之间吹气时,它们会彼此接近、碰撞。
