还有一个方法,可以计算出π的近似值,而且很有意思。
准备一些约2厘米长的缝衣针,把针尖去掉,使每根针的上下粗细一样。然后,在一张白纸上划出一些平行的直线,要求每两条直线之间的距离正好等于针长的两倍。接着,把这些针逐个从高处落到纸上,看看这些针有没有跟某一条直线交叉,如图(b)Ⅰ所示。为了保证针在落到纸面上的时候不会跳起来,最好在纸的下面铺一层厚纸,或者放一些呢绒。这样多做几次,比如,100次或者1000次,次数越多越好。这样做的时候,把每次是否跟直线交叉记录下来。完成一定的次数后,把这个总次数除以交叉的次数,得到的数值就是π的近似值。
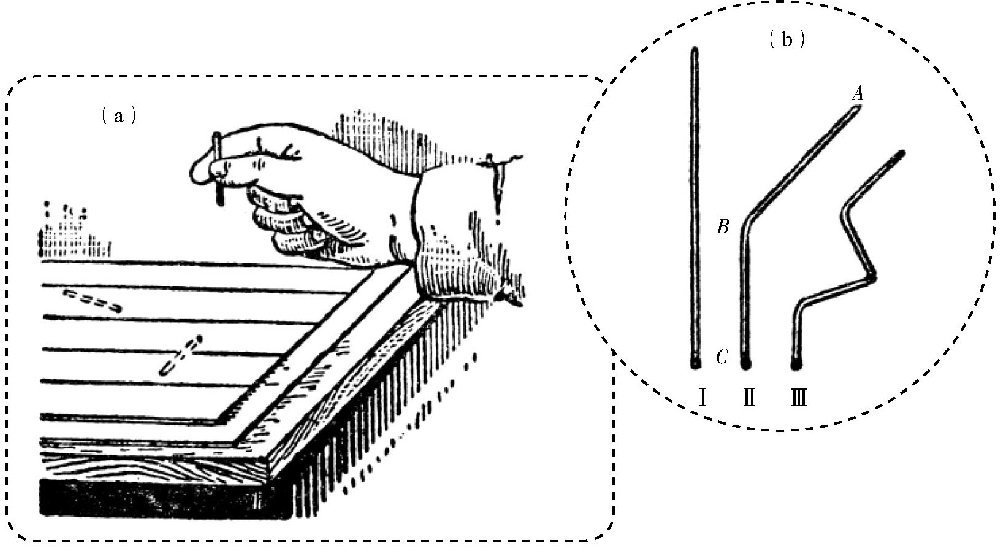
图 掷针实验。
这是为什么呢?下面我们就来解释一下。我们用K表示缝衣针和直线交叉的最可能次数。我们知道,针长是20毫米,那么当缝衣针和直线交叉时,这个交叉点必定是在这20毫米中的某一个点上,而且,对于这根针来说,这20毫米中的任何一点,或者说任何一毫米,跟别的点都具有同样的可能性。所以,每一毫米可能和直线交叉的次数就是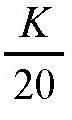
。如果针上某段的长度是3毫米,它可能和直线交叉的次数就是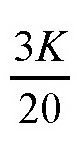
;如果长度是11毫米,它可能和直线交叉的次数就是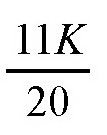
……也就是说,缝衣针可能和直线交叉的次数跟缝衣针的长度成正比。
这个比值的大小,跟缝衣针的形状没有关系,哪怕它是弯曲的,如图(b)Ⅱ所示。图中,AB段的长度是11毫米,BC段的长度是9毫米,那么AB段最可能的交叉次数是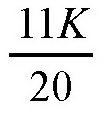
,BC段是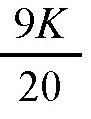
,如果是整根缝衣针,就是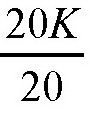
也就是K。我们甚至可以把针弯曲得更严重一些,如图(b)Ⅲ所示。不管形状是什么样的,交叉的次数都是一样的。需要注意的是,如果使用弯曲的缝衣针,它可能会同时在几个地方和直线交叉。这时,我们要把每一个交叉点作为一次。这是因为,每个交叉点都代表了某一段。
现在,我们假设把缝衣针弯成一个圆形,这个圆的直径正好等于两条直线之间的距离。也就是说,这个圆的直径是我们本篇开始时提到的缝衣针长的两倍。当这个圆环每次落下来的时候,肯定会和两条直线交叉,至少会有接触,总之,肯定每次都有2次交叉。假设落下来的总次数是N,那么总的交叉数就是2N。我们前面用到的直针长度比这个圆环要短,直针的长度跟圆环长度的比值,相当于圆环的半个直径跟圆环圆周长度的比值,也就是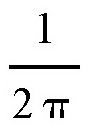
刚才,我们已经得出,最可能交叉的次数跟针的长度成正比,所以这个圆环最可能的交叉次数K跟2N的比值应该是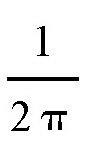
,而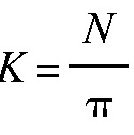
,所以我们有:

刚才已经提到,投掷的次数越多得到的结果越准确。据说,瑞士有一位天文学家叫沃尔夫,他观察了5000次,最后得到的π值是3.159,这个值只比阿基米德的差那么一点点。
现在,我们知道了,圆周跟直径的比值竟然可以用实验的方法得到。有意思的是,这个方法不需要画出图形,也不用画出圆的直径,甚至连圆规都不需要。即便是一个对几何学一窍不通、对圆没有一点儿概念的人,只要有耐心,进行很多次这样的实验,一样可以得到π的近似值。
