很多读者对古代力学家希罗设计的喷泉应当都不陌生。在谈论这种有趣装置的新形式之前,我们先来看一下它的构造。 如图所示,希罗喷泉由3个容器构成:上面的容器a没有盖子,而下面的两个容器b、c则是封闭的球形。这3个容器被3根管子连接在了一起。在容器a中注入部分的水,在b球装满水,c球里不装水,任其装满空气,就可以形成喷泉了:水会沿着管子从容器a流到容器c, c球中的空气就会排到b球中去。而b球里的水在空气的压力作用下,则会沿着管子往上流。于是,喷泉就在容器口形成了。如果b球里的水全部流完了,喷泉也就停止了。
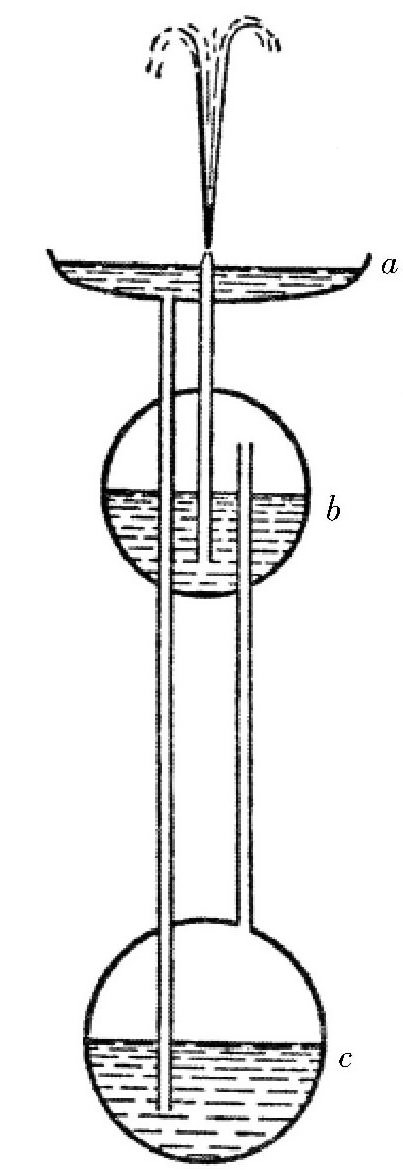
图 古老的希罗喷泉示意图。
古老的希罗喷泉就是这样设计的。到了后来,有一位意大利中学教师对希罗喷泉进行了改造。由于当时的物理实验室缺乏必要的设备,这位老师只能运用自己的聪明才智和非凡的创造力把希罗喷泉进行简化。最后,他想到了一个新式喷泉的设计方法,只需要使用简单的设备就能实现。如 图 所示,他用药瓶代替上面的球形容器,用橡皮管代替玻璃管或者金属管。而且上面的那个容器也可以不用穿孔,只要把橡皮管的一端放到里面就可以,就像图演示的那样。
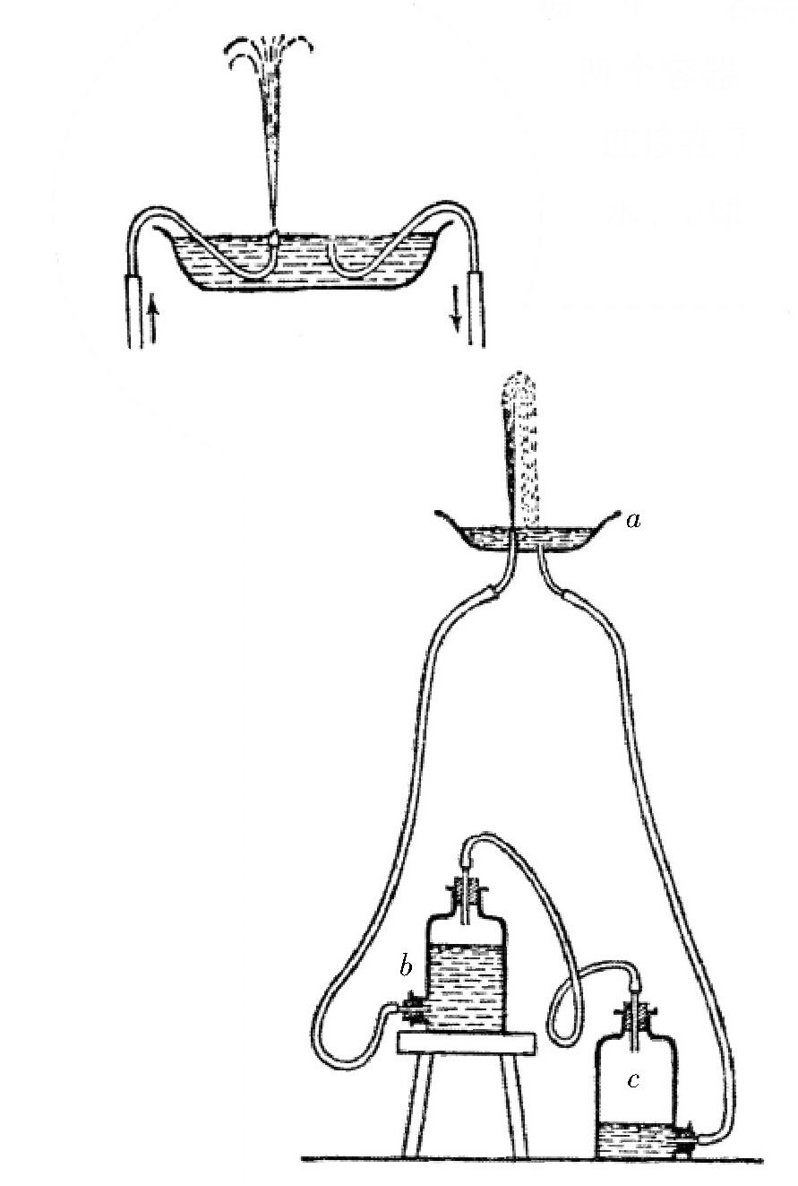
图 新式希罗喷泉示意图。
经过简单的改造后,仪器变得更加适用了。如果b瓶的水流经a碟,在全部流进了c瓶之后,只需要互换一下b和c两个瓶的位置,喷泉就会再次形成了。有一点不能忘记,要把喷嘴也同时移到另一条管子上去。
喷泉经过改造之后,还有另外一个便利之处,它可以通过随意改变容器的位置,来研究各个容器在位置不同时,对喷泉喷射高度变化的影响。
如果需要增大喷泉的喷射高度,只需要用水银(汞)来代替这个装置下面的两个瓶里的水,用水来代替空气(图 )。替换后的工作原理也很简单:水银从c瓶流进b瓶的时候,会把b瓶里的水排出去,喷泉也就形成了。我们知道,水银的重量是水的13.5倍,这样的话就可以算出喷泉在这时候的高度。我们分别用h1、h2、h3来表示这几个液面之间的高度差。现在,我们就来分析一下,c瓶里的水银受到了哪些力的作用,才流进了b瓶。
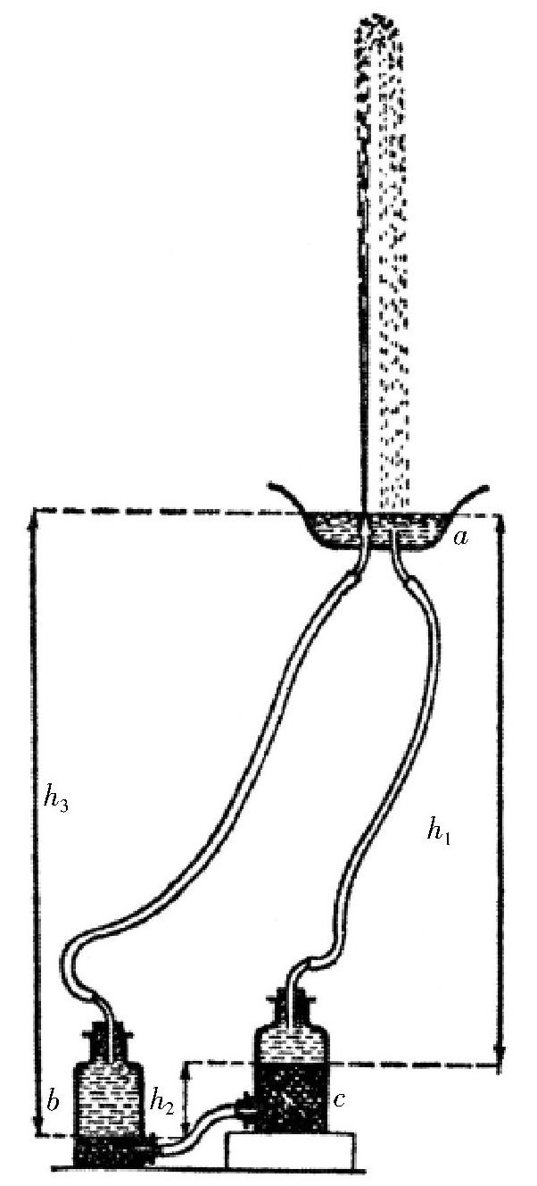
图 在水银的压力作用下,喷泉的喷射高度将大大提高。
首先,b、c两瓶的连接管里的水银受到了来自两端的压力。这一段水银受到的来自后面的作用力的大小等于高度为h2的汞柱的压力(h2汞柱的压力等于13.5h2个水柱的压力)与h1这么高的水柱的压力之和。水银受到的来自左边的作用力的大小为h3水柱的压力。综合计算,可以得出:水银受到的压力大小是(13.5h2+h1-h3)个水柱压力。
由于h3-h1=h2,所以(13.5h2+h1-h3)可以转换为:12.5h2。
由此可知,是一根高为12.5h2的水柱重量把水银压到了b瓶里。从理论上来讲,喷泉的最高点应该是b、c两个瓶里水银面高度差的12.5倍。可是因为有摩擦力的存在,喷泉的高度会稍微有所下降。
即使会有所下降,利用这个装置,我们还是能够得到喷射得比较高的喷泉。比如,如果我们把一个瓶移到比另一个瓶高大约1米的地方,喷泉的喷射高度就可以达到10米了。通过上面的计算,我们还可以发现一个有趣的现象,那就是喷泉的高度与碟a距离水银瓶的高度没有任何关系。
