很早的时候,古巴比伦人就发现,每隔18年零10天,就会出现一次日月食,他们把这一现象称为沙罗周期。古代人就是利用沙罗周期来预测日月食的。虽然很早就发现了沙罗周期,但直到近代,人们才研究出它出现的原因。

一个月指的是月球绕地球运行一周的时间。在天文学上,关于一个月,有5种不同的时间,下面,我们来看其中的两种:朔望月和交点月。
(1)朔望月。指的是两次相同的月面相位间隔的时间,也就是在太阳上看月球绕地球一周花的时间,它等于从上一次出现朔月开始到下一次再出现朔月的时间,为29.5306天。
(2)交点月。所谓“交点”,是指地球公转轨道跟月球绕地轨道的交点。从“交点”开始,月球绕地球一周后再返回“交点”的时间称为交点月。这个时间是27.2123天。
日食和月食形成的条件之一就是朔月或望月正好落在交点上,这时月球中心、地球中心和太阳中心正好在一条直线上。也就是说,从这一次月食开始,到下次再出现同样的月食,间隔的时间必定包含整数个朔望月和整数个交点月。
可以通过下面的方程来计算这一间隔时间:
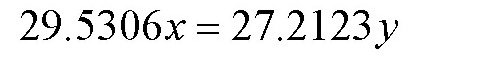
其中,x、y为整数。把这个方程改写成比例式:
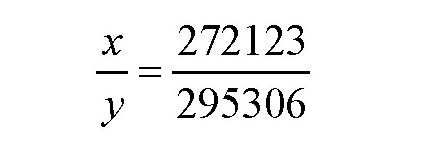
在上述比例式中,29.5306和27.2123没有公约数,所以,最小的整数答案为:
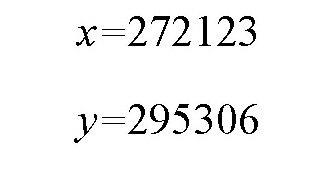
单从这两个数看,就是几万年的时间,这样对我们预测日月食,没有任何作用,所以,天文学家通常取它们的近似值:
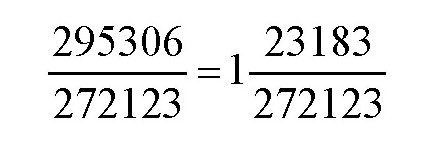
在剩下的分数中用分子和分母除以分子:
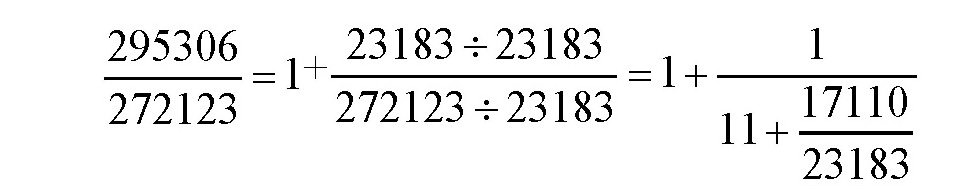
再把分数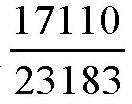
的分子和分母除以分子,一直进行下去,就可以得到下面的式子:
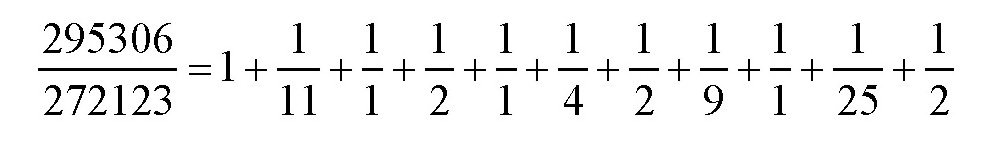
我们只取前面的几节,得到一些近似值:
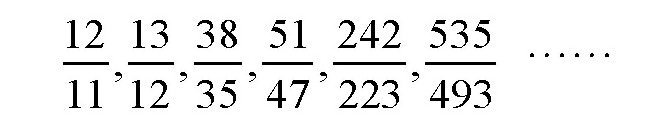
计算到第五个近似值,对我们来说就足够了,它已经非常精确,当然,如果继续往后计算,将更加准确。如果采用这组数值,即x=223,y=242,那么,可以计算出日月食的重复周期是223个朔望月,或者242个交点月。如果换算成年,就是18年零11.3天或者10.3天(在这个时期,有可能有4个或者5个闰年)。
前面讨论的就是沙罗周期的原理。根据计算可以看出,这个原理并不是非常准确。所以,我们会把沙罗周期减掉0.3天,以18年零10天为准,根据它计算出的第二次出现同样日月食的时间比实际情况差不多要晚8个小时。
如果重复使用3次沙罗周期来计算,得出的结果跟实际情况正好差一天。月球到地球的距离和地球到太阳的距离都是变化着的,并呈一定的周期性,对于这一点,在沙罗周期中并没有体现。也就是说,利用沙罗周期,只能推算出下次发生日月食时是哪一天,却无法预测会发生月偏食、月全食,还是月环食,更无法预测在地球的哪些地区可以看到它。另外,也有可能上一次出现的日偏食面积非常小,但18年后出现的日食由于面积太小了,以致我们根本看不见。而且,也有可能发生相反的情况:18年前根本没看到日食,18年后,人们却在同一天看到了很小的日偏食。
随着科学的发展,天文学家们已经对月球的运动研究得非常透彻,甚至可以推测出发生日月食的准确时间,前后相差不超过一秒钟,沙罗周期因此退出了历史舞台。
