当一个圆沿着跟它处于同一平面的某条直线滚动时,这个圆上的每一个点都会跟这个平面接触。一般来说,这个圆有自己的轨迹。
假如我们研究一下一个圆沿着一条直线或圆周运行的轨迹,我们就会发现,有很多种不同的曲线。如图和图所示在,它们是其中的两种曲线。
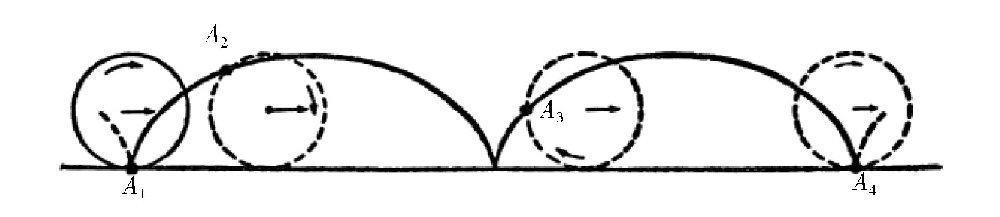
图 圆周上的点A沿直线作无滑动的转动时的转动轨迹。
在图中,我们会遇到这样的问题:当一个小圆在另一个大圆的圆周内侧滚动时,它上面的某一个点能否画出一条直线轨迹,而不是曲线轨迹呢?初看这个问题,好像是不可能的。
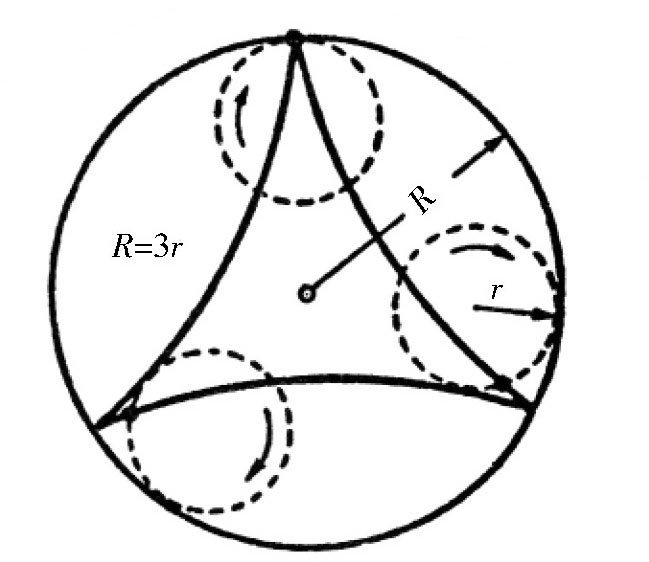
图 小圆在一个大圆内测滚动时,某点所形成的轨迹。这里R=3r。
不过,我曾经亲眼看到过这样的运行图。
在图中是一个玩具,有人称它为“吊索人偶”。读者朋友们也可以很容易做出一个这样的玩具来。找一块儿厚的硬纸板或木板,在上面画出一个直径为30厘米的圆,注意要把圆画在纸板的中央,也就是在纸板的四周要留一些空白,然后画出圆的直径,并把它向两边延长。
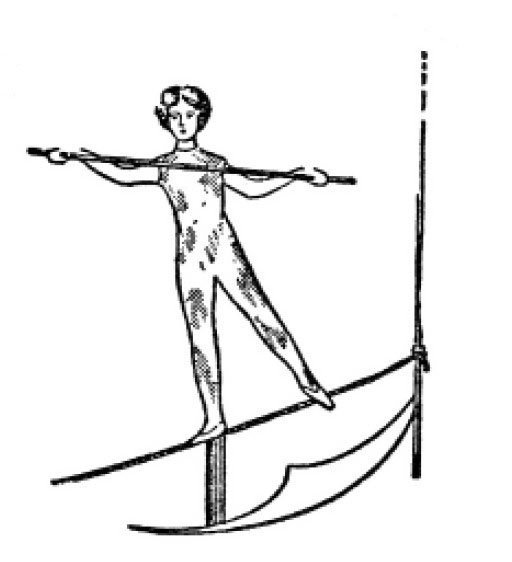
图 钢索人偶。
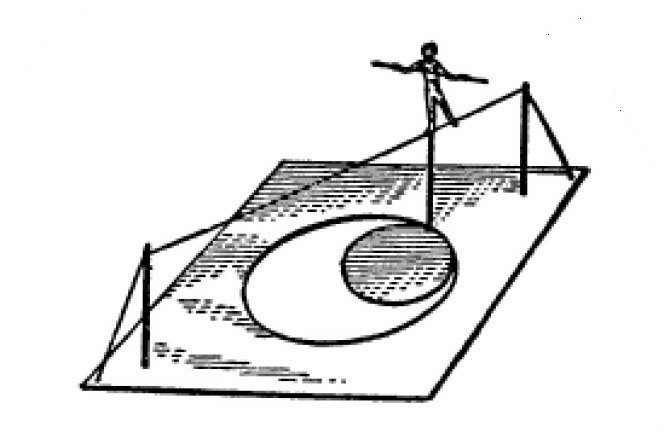
图 在滚动着的圆形上沿着直线移动的人偶。
如图所示,画出直径延长线,在圆的两边分别插上一根缝衣针。再找一根细绳,把它穿进两根针的孔里。拉紧细绳,将绳子的两头固定在纸板的两边。然后,把刚开始画出来的圆用剪刀剪下来,这样纸板上就出现了一个直径30厘米的大圆孔。再找一块硬纸板或者木板,在上面画一个直径15厘米的圆,并把它剪下来。把这个小圆放到大圆孔中。在这个小圆的边上,插上一根缝衣针。再用刚才剩下的纸板剪出一个人物形象,把它的脚固定在这根缝衣针的尖上。
如果我们把这个小圆紧贴着大圆的内侧滚动,就会发现小圆上的缝衣针和人物会沿着那条绷紧的细绳前后移动。关于这个现象,我们可以这样解释:当小圆滚动时,小圆上插了缝衣针的那个点在完全沿着大圆的直径滚动。
但是,在图所示的情况下,滚动的圆上的点为什么没有沿着直线移动,而是走出了一条曲线呢?一般来说,我们把这条曲线称为圆内旋轮线。其实,这是由大圆和小圆直径的比值决定的。
【题目】请证明:当一个小圆在另一个大圆周内滚动时,如果它们直径的比值是1∶2,那么在小圆滚动时,它上面的点将沿着大圆周的直径做直线运动。
【解答】如图所示,我们假设大圆O的直径是小圆O1的直径的2倍,那么当小圆O1滚动时,不管它滚动到什么地方,在它的圆周上,总有一个点在大圆O的圆心。
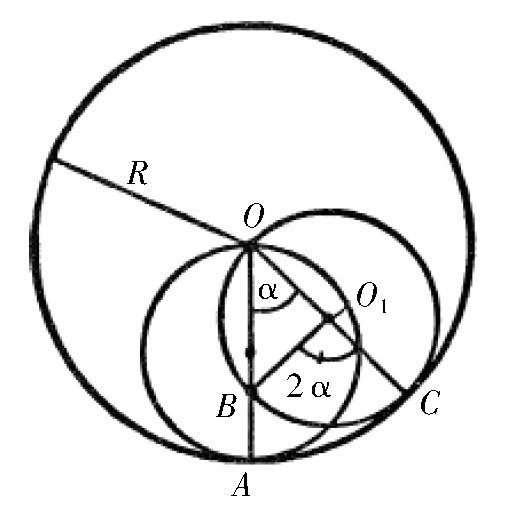
图 “吊索人偶”的几何学图示。
现在,我们就来看看小圆上的点A移动的情形。不妨假设在某一时刻,小圆沿着弧线AC滚动。那么,当小圆O1在这个位置上的时候,点A会在什么地方?很明显,它应该处于圆周上的点B上。这时,弧线AC和BC的长度相等。
假设OA=R,∠AOC=α,那么,我们有AC=R×α。所以,BC也等于及R×α,而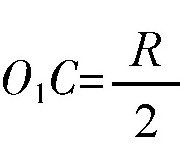
,所以:
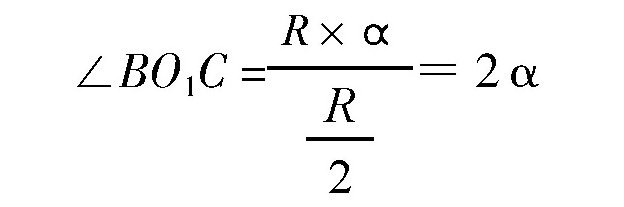
而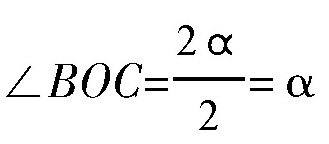
,也就是说,点B仍然在直线OA上。
实际上,刚才介绍的这个玩具,就是把旋转运动变成了直线运动。
